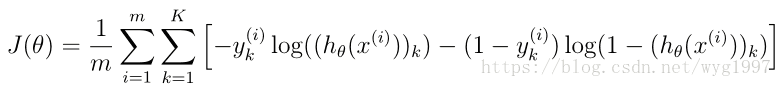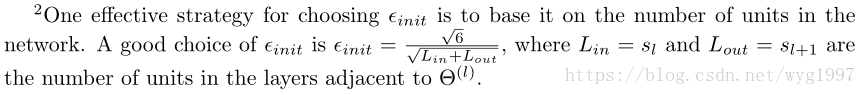吳恩達機器學習 - 神經網路的反向傳播演算法 吳恩達機器學習 - 神經網路的反向傳播演算法
阿新 • • 發佈:2018-11-05
原
視覺化隱藏層(使用
吳恩達機器學習 - 神經網路的反向傳播演算法
2018年06月21日 20:59:35 離殤灬孤狼 閱讀數:373<span class="tags-box artic-tag-box"> <span class="label">標籤:</span> <a data-track-click="{"mod":"popu_626","con":"機器學習"}" class="tag-link" href="http://so.csdn.net/so/search/s.do?q=機器學習&t=blog" target="_blank">機器學習 </a><a data-track-click="{"mod":"popu_626","con":"神經網路"}" class="tag-link" href="http://so.csdn.net/so/search/s.do?q=神經網路&t=blog" target="_blank">神經網路 </a> <span class="article_info_click">更多</span></span> <div class="tags-box space"> <span class="label">個人分類:</span> <a class="tag-link" href="https://blog.csdn.net/wyg1997/article/category/7742222" target="_blank">吳恩達機器學習 </a> </div> </div> <div class="operating"> </div> </div> </div> </div> <article> <div id="article_content" class="article_content clearfix csdn-tracking-statistics" data-pid="blog" data-mod="popu_307" data-dsm="post" style="height: 2211px; overflow: hidden;"> <div class="article-copyright"> 版權宣告:如果感覺寫的不錯,轉載標明出處連結哦~blog.csdn.net/wyg1997 https://blog.csdn.net/wyg1997/article/details/80766153 </div> <div class="markdown_views"> <!-- flowchart 箭頭圖示 勿刪 --> <svg xmlns="http://www.w3.org/2000/svg" style="display: none;"><path stroke-linecap="round" d="M5,0 0,2.5 5,5z" id="raphael-marker-block" style="-webkit-tap-highlight-color: rgba(0, 0, 0, 0);"></path></svg> <p>題目連結:<a href="https://s3.amazonaws.com/spark-public/ml/exercises/on-demand/machine-learning-ex4.zip" rel="nofollow" target="_blank">點選開啟連結</a></p>
筆記:

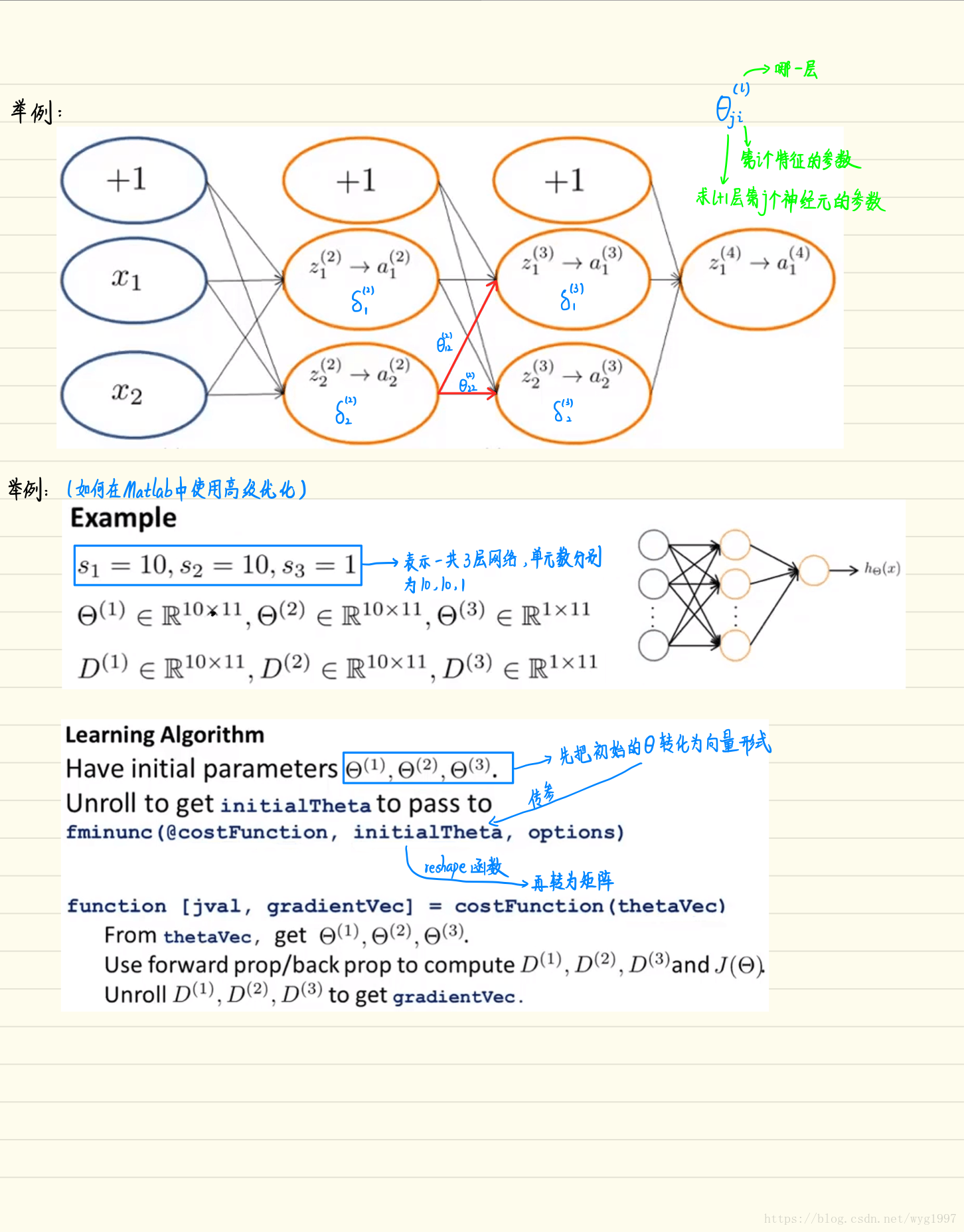
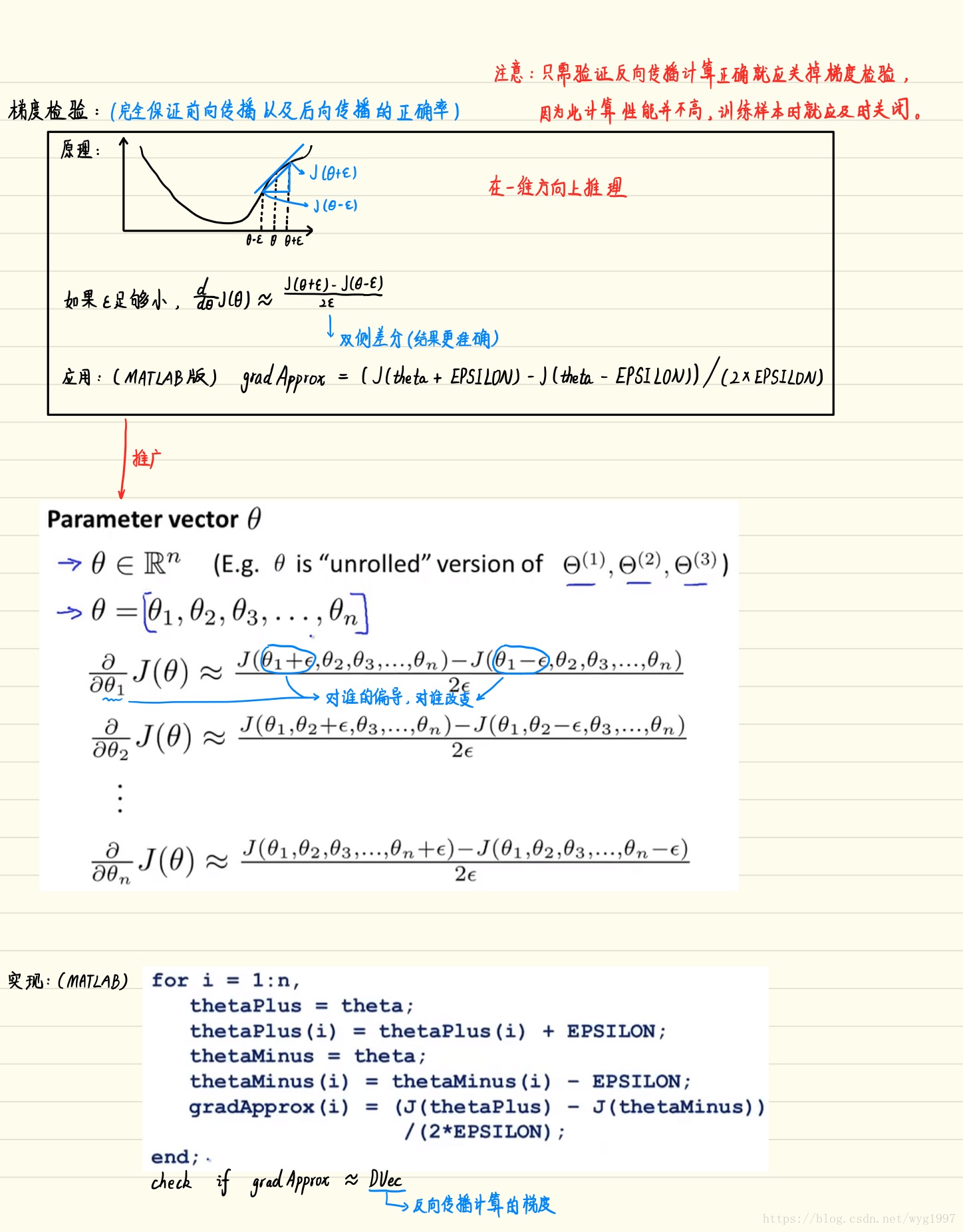

因為這一部分的內容確實難度比較大,所以我準備按最後一頁筆記的思路一點一點的寫出實現的思路和我的想法。
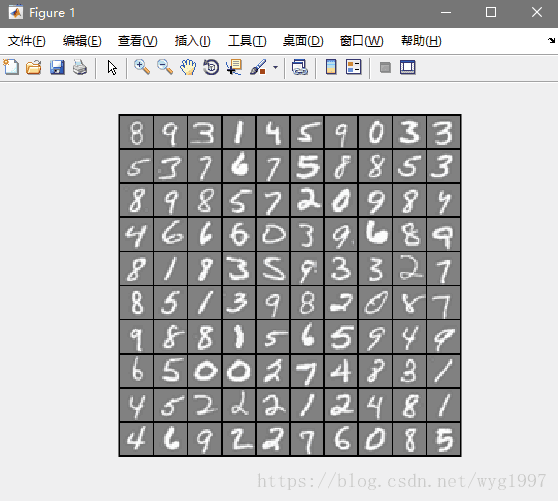
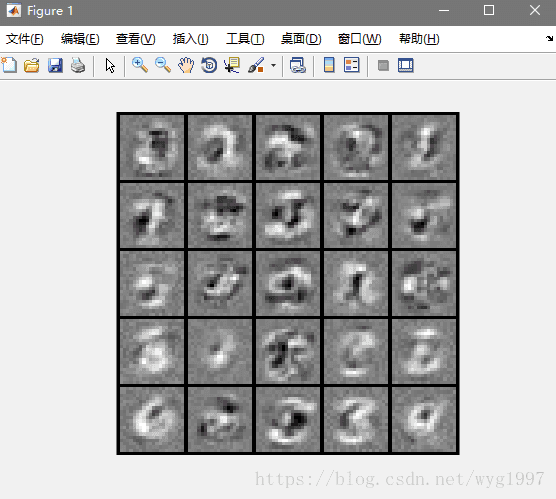
首先讓資料視覺化
執行程式碼
load('ex4data1.mat');
m = size(X, 1);
sel = randperm(size(X, 1)); %亂序後隨機選擇100組資料進行展示
sel = sel(1:100);
displayData(X(sel, :));
- 1
- 2
- 3
- 4
- 5
- 6
- 7
結果是:
用到是函式是displayData.m:
function [h, display_array] = displayData(X, example_width)
%DISPLAYDATA Display 2D data in a nice grid
% [h, display_array] = DISPLAYDATA(X, example_width) displays 2D data
% stored in X in a nice grid. It returns the figure handle h and the
% displayed array if requested.
% Set example_width automatically if not passed in
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
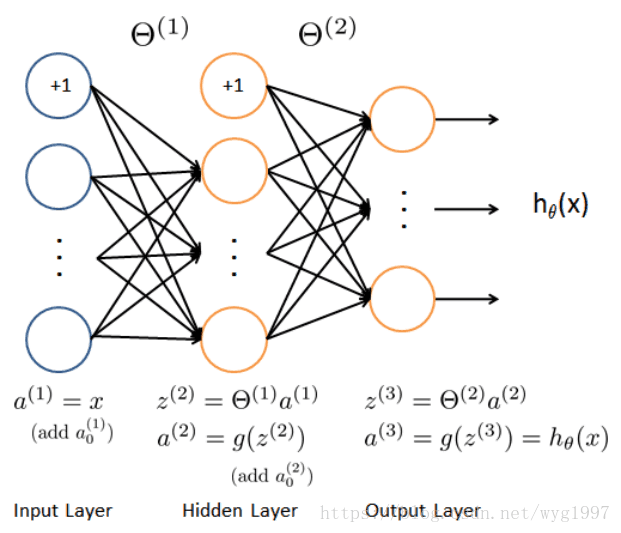
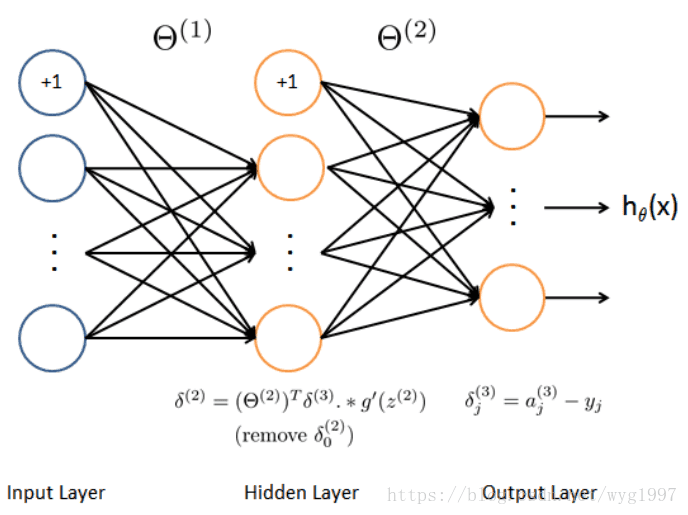
表示一下神經網路模型:
我們可以得到以下資訊:
- 3層網路
- 輸入層有400(20*20的影象樣本)個單元(這裡不包括偏置單元)
- 輸出層有10個(表示0,1,2,…,9)單元
- 隱藏層有25個單元
代價函式
公式
sigmoid.m程式碼(這個已經沒有難度,只是下面要呼叫,先粘出來):
function g = sigmoid(z)
%SIGMOID Compute sigmoid functoon
% J = SIGMOID(z) computes the sigmoid of z.
g = 1.0 ./ (1.0 + exp(-z));
end
- 1
- 2
- 3
- 4
- 5
- 6
代價函式的計算:nnCostFunction.m中填充的程式碼(暫時沒加正則化)(這裡要求有任意維度的輸出層都通用):
%計算各層的z(x)
a1 = [ones(m,1), X]; %input
z2 = a1*Theta1'; %hidden
a2 = [ones(m,1), sigmoid(z2)];
z3 = a2*Theta2'; %output
a3 = sigmoid(z3);
%轉換y向量
Y = zeros(m, size(Theta2, 1)); %適應不同維度的輸出層
for i = 1:size(Theta2, 1)
Y(find(y==i), i) = 1;
end
%然後計算J
J = sum(sum(-(Y.*log(a3)+(1-Y).*log(1-a3))))/m;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
代價函式正則化(在上面的程式碼下新增):
%對J進行正則化
J = J + lambda/(2.0*m)* ...
(sum(sum(Theta1(:,2:size(Theta1,2)).^2))+ ...
sum(sum(Theta2(:,2:size(Theta2,2)).^2)));
- 1
- 2
- 3
- 4
反向傳播
Sigmoid導數的實現(sigmoidGradient.m):
function g = sigmoidGradient(z)
%SIGMOIDGRADIENT returns the gradient of the sigmoid function
%evaluated at z
% g = SIGMOIDGRADIENT(z) computes the gradient of the sigmoid function
% evaluated at z. This should work regardless if z is a matrix or a
% vector. In particular, if z is a vector or matrix, you should return
% the gradient for each element.
g = zeros(size(z));
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the gradient of the sigmoid function evaluated at
% each value of z (z can be a matrix, vector or scalar).
g = sigmoid(z).*(1-sigmoid(z));
% =============================================================
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
隨機初始化(randInitializeWeights.m)(因為權重不能全為0嘛,筆記上解釋了為什麼):
function W = randInitializeWeights(L_in, L_out)
%RANDINITIALIZEWEIGHTS Randomly initialize the weights of a layer with L_in
%incoming connections and L_out outgoing connections
% W = RANDINITIALIZEWEIGHTS(L_in, L_out) randomly initializes the weights
% of a layer with L_in incoming connections and L_out outgoing
% connections.
%
% Note that W should be set to a matrix of size(L_out, 1 + L_in) as
% the first column of W handles the "bias" terms
%
% You need to return the following variables correctly
W = zeros(L_out, 1 + L_in);
% ====================== YOUR CODE HERE ======================
% Instructions: Initialize W randomly so that we break the symmetry while
% training the neural network.
%
% Note: The first column of W corresponds to the parameters for the bias unit
%
epsilon_init = 0.12; %這個數字要小一點從而保證較高的學習效率
W = rand(L_out, 1+L_in)*2*epsilon-epsilon_init;
% =========================================================================
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
另外這裡還有一個比較好的選取epsilon的方法:
反向傳播(填充在nnCostFunction.m中,代價函式計算程式碼之下,注意這裡沒有正則化):
公式和圖示:
%開始反向傳播,分5部計算梯度
%1.對於輸入層,計算每個樣本的啟用值(上面已經實現)
%2.計算輸出層的誤差值
delta3 = a3 - Y;
%3.計算l=2層的誤差值(這裡由於矩陣的方向的不同,和文件中式子不太一樣)
delta2 = delta3*Theta2(:,2:end).*sigmoidGradient(z2);
%4.用公式計算DELTA(delta的大寫形式)
DELTA1 = delta2'*a1;
DELTA2 = delta3'*a2;
%5.除以樣本數得到梯度
Theta1_grad = DELTA1./m;
Theta2_grad = DELTA2./m;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
梯度檢驗(checkNNGradients.m):
function checkNNGradients(lambda)
%CHECKNNGRADIENTS Creates a small neural network to check the
%backpropagation gradients
% CHECKNNGRADIENTS(lambda) Creates a small neural network to check the
% backpropagation gradients, it will output the analytical gradients
% produced by your backprop code and the numerical gradients (computed
% using computeNumericalGradient). These two gradient computations should
% result in very similar values.
%
if ~exist('lambda', 'var') || isempty(lambda)
lambda = 0;
end
input_layer_size = 3;
hidden_layer_size = 5;
num_labels = 3;
m = 5;
% We generate some 'random' test data
Theta1 = debugInitializeWeights(hidden_layer_size, input_layer_size);
Theta2 = debugInitializeWeights(num_labels, hidden_layer_size);
% Reusing debugInitializeWeights to generate X
X = debugInitializeWeights(m, input_layer_size - 1);
y = 1 + mod(1:m, num_labels)';
% Unroll parameters
nn_params = [Theta1(:) ; Theta2(:)];
% Short hand for cost function
costFunc = @(p) nnCostFunction(p, input_layer_size, hidden_layer_size, ...
num_labels, X, y, lambda);
[cost, grad] = costFunc(nn_params);
numgrad = computeNumericalGradient(costFunc, nn_params);
% Visually examine the two gradient computations. The two columns
% you get should be very similar.
disp([numgrad grad]);
fprintf(['The above two columns you get should be very similar.\n' ...
'(Left-Your Numerical Gradient, Right-Analytical Gradient)\n\n']);
% Evaluate the norm of the difference between two solutions.
% If you have a correct implementation, and assuming you used EPSILON = 0.0001
% in computeNumericalGradient.m, then diff below should be less than 1e-9
diff = norm(numgrad-grad)/norm(numgrad+grad);
fprintf(['If your backpropagation implementation is correct, then \n' ...
'the relative difference will be small (less than 1e-9). \n' ...
'\nRelative Difference: %g\n'], diff);
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
好了,檢驗通過我們進行下一步:正則化梯度(nnCostFunction.m)(在上面計算梯度的程式碼下填充):
%正則化梯度
Theta1_grad(:,2:end) = Theta1_grad(:,2:end) + lambda/m*Theta1(:,2:end);
Theta2_grad(:,2:end) = Theta2_grad(:,2:end) + lambda/m*Theta2(:,2:end);
- 1
- 2
- 3
到此為止,計算代價以及計算梯度的過程我們已經完成了,下面貼出nnCostFunction.m的完整程式碼:
function [J grad] = nnCostFunction(nn_params, ...
input_layer_size, ...
hidden_layer_size, ...
num_labels, ...
X, y, lambda)
%NNCOSTFUNCTION Implements the neural network cost function for a two layer
%neural network which performs classification
% [J grad] = NNCOSTFUNCTON(nn_params, hidden_layer_size, num_labels, ...
% X, y, lambda) computes the cost and gradient of the neural network. The
% parameters for the neural network are "unrolled" into the vector
% nn_params and need to be converted back into the weight matrices.
%
% The returned parameter grad should be a "unrolled" vector of the
% partial derivatives of the neural network.
%
% Reshape nn_params back into the parameters Theta1 and Theta2, the weight matrices
% for our 2 layer neural network
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)), ...
hidden_layer_size, (input_layer_size + 1));
Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), ...
num_labels, (hidden_layer_size + 1));
% Setup some useful variables
m = size(X, 1);
% You need to return the following variables correctly
J = 0;
Theta1_grad = zeros(size(Theta1));
Theta2_grad = zeros(size(Theta2));
% ====================== YOUR CODE HERE ======================
% Instructions: You should complete the code by working through the
% following parts.
%
% Part 1: Feedforward the neural network and return the cost in the
% variable J. After implementing Part 1, you can verify that your
% cost function computation is correct by verifying the cost
% computed in ex4.m
%
% Part 2: Implement the backpropagation algorithm to compute the gradients
% Theta1_grad and Theta2_grad. You should return the partial derivatives of
% the cost function with respect to Theta1 and Theta2 in Theta1_grad and
% Theta2_grad, respectively. After implementing Part 2, you can check
% that your implementation is correct by running checkNNGradients
%
% Note: The vector y passed into the function is a vector of labels
% containing values from 1..K. You need to map this vector into a
% binary vector of 1's and 0's to be used with the neural network
% cost function.
%
% Hint: We recommend implementing backpropagation using a for-loop
% over the training examples if you are implementing it for the
% first time.
%
% Part 3: Implement regularization with the cost function and gradients.
%
% Hint: You can implement this around the code for
% backpropagation. That is, you can compute the gradients for
% the regularization separately and then add them to Theta1_grad
% and Theta2_grad from Part 2.
%
%本地資料的矩陣大小
%Theta1:25*401
%Theta2:10*26
%X:5000*400
%z1:5000*401
%z2:5000*25
%z3:5000*10
%y:5000*1
%Y:5000*10
%a1:5000*401
%a2:5000*26
%a3:5000*10
%delta3:5000*10
%delta2:5000*25
%計算各層的z(x)
a1 = [ones(m,1), X]; %input
z2 = a1*Theta1'; %hidden
a2 = [ones(m,1), sigmoid(z2)];
z3 = a2*Theta2'; %output
a3 = sigmoid(z3);
%轉換y向量
Y = zeros(m, size(Theta2, 1)); %適應不同維度的輸出層
for i = 1:size(Theta2, 1)
Y(find(y==i), i) = 1;
end
%然後計算J
J = sum(sum(-(Y.*log(a3)+(1-Y).*log(1-a3))))/m;
%對J進行正則化
J = J + lambda/(2.0*m)* ...
(sum(sum(Theta1(:,2:size(Theta1,2)).^2))+ ...
sum(sum(Theta2(:,2:size(Theta2,2)).^2)));
%開始反向傳播,分5部計算梯度
%1.對於輸入層,計算每個樣本的啟用值(上面已經實現)
%2.計算輸出層的誤差值
delta3 = a3 - Y;
%3.計算l=2層的誤差值(這裡由於矩陣的方向的不同,和文件中式子不太一樣)
delta2 = delta3*Theta2(:,2:end).*sigmoidGradient(z2);
%4.用公式計算DELTA(delta的大寫形式)
DELTA1 = delta2'*a1;
DELTA2 = delta3'*a2;
%5.除以樣本數得到梯度
Theta1_grad = DELTA1./m;
Theta2_grad = DELTA2./m;
%正則化梯度
Theta1_grad(:,2:end) = Theta1_grad(:,2:end) + lambda/m*Theta1(:,2:end);
Theta2_grad(:,2:end) = Theta2_grad(:,2:end) + lambda/m*Theta2(:,2:end);
% -------------------------------------------------------------
% =========================================================================
% Unroll gradients
grad = [Theta1_grad(:) ; Theta2_grad(:)];
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
學習使用高階優化來求解(如果對寫法有疑惑,可以參考這篇文章:點選開啟連結):
% Create "short hand" for the cost function to be minimized
costFunction = @(p) nnCostFunction(p, ...
input_layer_size, ...
hidden_layer_size, ...
num_labels, X, y, lambda);
% Now, costFunction is a function that takes in only one argument (the
% neural network parameters)
[nn_params, cost] = fmincg(costFunction, initial_nn_params, options);
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
視覺化隱藏層(使用displayData(Theta1(:, 2:end));):
displayData.m:
function [h, display_array] = displayData(X, example_width)
%DISPLAYDATA Display 2D data in a nice grid
% [h, display_array] = DISPLAYDATA(X, example_width) displays 2D data
% stored in X in a nice grid. It returns the figure handle h and the
% displayed array if requested.
% Set example_width automatically if not passed in
if ~exist('example_width', 'var') || isempty(example_width)
example_width = round(sqrt(size(X, 2)));
end
% Gray Image
colormap(gray);
% Compute rows, cols
[m n] = size(X);
example_height = (n / example_width);
% Compute number of items to display
display_rows = floor(sqrt(m));
display_cols = ceil(m / display_rows);
% Between images padding
pad = 1;
% Setup blank display
display_array = - ones(pad + display_rows * (example_height + pad), ...
pad + display_cols * (example_width + pad));
% Copy each example into a patch on the display array
curr_ex = 1;
for j = 1:display_rows
for i = 1:display_cols
if curr_ex > m,
break;
end
% Copy the patch
% Get the max value of the patch
max_val = max(abs(X(curr_ex, :)));
display_array(pad + (j - 1) * (example_height + pad) + (1:example_height), ...
pad + (i - 1) * (example_width + pad) + (1:example_width)) = ...
reshape(X(curr_ex, :), example_height, example_width) / max_val;
curr_ex = curr_ex + 1;
end
if curr_ex > m,
break;
end
end
% Display Image
h = imagesc(display_array, [-1 1]);
% Do not show axis
axis image off
drawnow;
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59