補碼-加法與減法運算
基本的規則: ①加法:
| 整數: [A]補 + [B]補 = [A+B]補 (mod 2^(n+1)) |
| 小數: [A]補 + [B]補 = [A+B]補 (mod 2) |
②減法:
| 整數: [A-B]補 = [A]補 + [-B]補 (mod 2^(n+1)) |
| 小數: [A-B]補 = [A]補 + [-B]補(mod 2) |
注:
| 整數的補碼是它本身; |
| [-B]補的求法就是 [B]補的連同符號位在內,每位取反,末位加一。 |
Example1:相加 -8到+3(機器數字長為8位)
(+3) 0 0 0 0 0 0 1 1
+(−8) 1 1 1 1 1 0 0 0
Example2:相加 -5到-2(機器數字長為8位)
(−2) 1 1 1 1 1 1 1 0+(−5) 1 1 1 1 1 0 1 1-------------------------------------
(-7)1 1 1 1 1 1 0 0 1 (按模
Example3:已知A = -1001,B = -0101,求[A + B]補
過程:
從第一位開始加,1 + 1 = 10(滿2進10);
第二位:1+1+1 = 11;
第三位:1 +1 + 0 = 10;
第四位:1 +0 + 1 = 10;
第五位:1 +1 + 1 = 11;
第六位:1,去掉。
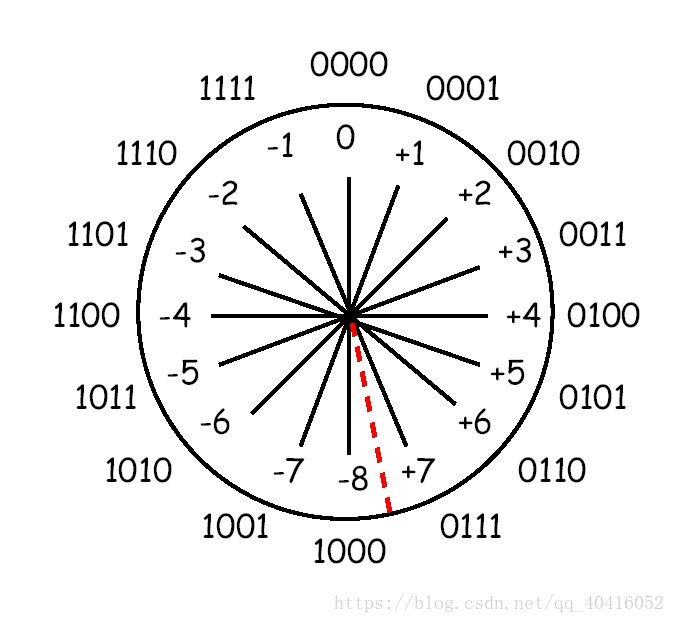
4位二進位制補碼數的數字圓:
可以通過圍繞數字圓圈移動來新增或減去數字
- 順時針新增
- 逆時針減法(新增負數)
Example4:求1,0100011 - 1,1010011
1, 0 1 0 0 0 1 1
- 0, 0 1 0 1 1 0 1
=0, 1 1 1 0 1 1 0
過程:
從第一位開始減,1-1 = 0;
第二位:1-0 = 1;
第三位:0-1 = 1,且第四位有1的負債(不看存款); 第四位:存款是0,負債是1,那麼自己就是-1啊,減不動1,於是借來2,先還負債,剩下1,再減1 = 0; 第五位:也負債1,借來1,減的是0所以還剩1; 第六位:本來是1,被第五位借走了,所以只剩0了,減不動1,所以向第七位借來2,減去1還剩1; 第七位:本身是0,被第六位借走了1,所以是-1,要減0,先借來2,還債後剩1,減0還是1 第八位:本身是1,被借走了,好嘛,那就 剩0了,剛好需要減的也是0,不要再往上借了。當然,需要借的時候也行,那個超出 八位以後的東西,從虛空中拿來,不用還!
Reference :