對於數在計算機裡的加減法，由於有了補碼這個編碼之後，其在計算機裡的加減法就變得容易許多，畢竟減法用補碼處理的時候可以轉化為加法解決，這也是為什麼不直接用原碼處理加減法的一個原因，在這裡分別對這兩個基礎運算作簡要說明，好為定點乘除法的說明做好基礎：

       1，補碼加法：

                   一個式子就可以解決問題——  [ x ]補  +  [ y ]補 =  [ x + y ]補                (mod 2^(n+1))     ……   ①

        這個式子的證明很簡單，但感覺比較繁瑣，可以借鑑《計算機組成原理》這本書，裡面有對該式的分類討論證明，這個式子要注意的地方就是末尾的(mod 2^(n+1)), 式①

                  例 1 ：   x = +1011, y = -0101,  求 x + y。

                        解 [ x ]補  = 01011, [ y ]補 = 11011

                                                 [ x ]補          01011

                                          +      [ y ]補           11011

                                       ——————————

                                            [ x + y ]補        100110

                         注意[ x + y ]補  得出的結果裡最左邊的1，這個1在(mod 2^(n+1))的條件下是會被省略的，所以此題的結果為 ： [ x + y ]補   = 00110，然後符號位為零，故結果為正數，所以  x + y = + 0110 。而且由此我們還可以得出補碼加減運算的一個規律那就是符號位產生的進位是要直接省去的。

       2，補碼減法 ：

                    也是一個式子解決問題—— [ x - y ]補 =  [ x ]補 -[ y ]補  = [ x ]補 + [ -y ]補……  ②

                                         [ - y ]補  =  乛 [y]補  + 2^(-n) ……  ③ (符號乛 表示對[y]補 作包括符號位在內的求反操作，+ 2^(-n)表示最末尾加1)

       式③是求式②的關鍵，這樣就可以在知道兩個數補碼的條件下做兩個數的減法運算，而且式②③也是要在(mod 2^(n+1))的情況下才能成立的，所以將兩個數的補碼做減法時符號位上的進位同樣要省去。

                     例 2 ：   x = +1101, y = +0110,  求 x - y。

                        解 [ x ]補  = 01101, [ y ]補 = 00110， [ -y ]補 = 11010

                                                 [ x ]補          01101

                                          +    [ - y ]補           11010

                                       ——————————

                                             [ x - y ]補        100111

                           故： x - y = + 0111

        3，加減運算溢位：

                   定點運算值是有範圍的，運算結果超出範圍就是溢位，對於溢位有正溢位和負溢位兩類，並在此強調一下判斷的溢位的兩類常用方法：

                ① 變形補碼法：之所以稱之為變形補碼，其實就是在原先只有一位標記符號位的基礎上在加一位標記符號位，那麼正數的符號位00，負數的符號位為11，在進行補碼加減法運算時兩個符號位均要參與運算，若結果的符號位為01，則發生正溢位，為10則發生負溢位，其他情況則沒有溢位。但無論最後結果的符號位是多少，真正的結果符號一定與最高符號位表示一致，下面兩個例子是以用變形補碼錶示法來進行加法運算的：

                        例 3 ：   x = +1100, y = +1000,  求 x + y。

                        解 [ x ]補  = 001100, [ y ]補 = 001000

                                                 [ x ]補          001100

                                          +      [ y ]補           001000

                                         ——————————

                                            [ x + y ]補            010100

                       結果符號位為01，故發生正溢位，但結果正確符號位與最高符號位一致，即0故結果應為正數。

                       例 4 ：   x = -1100, y = -1000,  求 x + y。

                        解 [ x ]補  = 110100, [ y ]補 = 111000

                                                 [ x ]補          110100

                                          +      [ y ]補           111000

                                         ——————————

                                            [ x + y ]補            101100

                       結果符號位為10，故發生負溢位，但結果正確符號位與最高符號位一致，即1故結果應為負數。

           所以在計算機中可以通過V = Sf1 ⊕Sf2，來判斷是否發生溢位，若v為1，則溢位，否則未溢位。其中Sf1和Sf2分別表示最高符號位和第二符號位。(⊕表示異或運算)

                     ②單符號位法，從以上兩個例子可以看出，當最高數值位產生進位，而符號位沒產生進位時，產生正溢位，當最高數值位沒進位，而符號位進位時，產生負溢位，故可用V =cf ⊕c0 來判斷是否運算髮生溢位，其中cf為符號位進位，c0為最高數值位進位。V為1表示發生溢位，V為0表示未發生溢位。

         4，行波進位的補碼加/減法器：

              說到行波進位的補碼加/減法器，我們先可以從一位全加器開始討論，假設Ai，Bi, Ci 分別表示當前位的兩個加數，以及前一位進位到當前位的進位，Si為和，C(i+1)為進位到下一位的進位，那麼可以得到所有情況下各變數的取值表，即它們的真值表:

                    所以可以由此得到邏輯表示式：                                                

                                                                   Si＝Ai⊕Bi⊕Ci

                                                                   Ci＋1＝AiBi＋BiCi＋CiAi

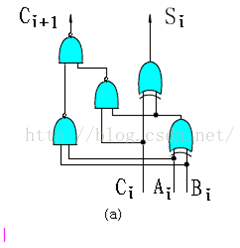
                    故由此可以得到一位全加器的邏輯電路圖:

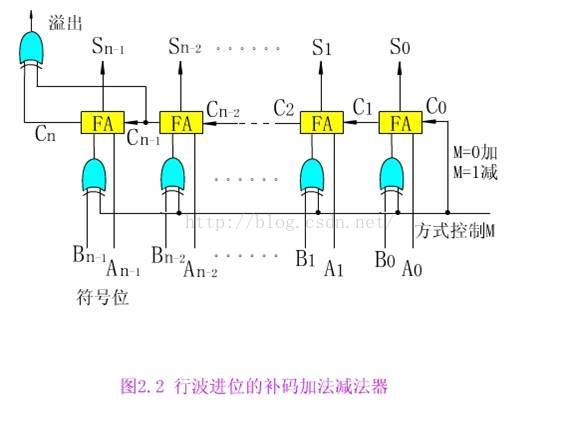
                       再由此就可以得出行波進位的補碼加/減法器的邏輯電路圖：

                     這張圖的總控線是M,M=0時，做加法運算，M=1時，做減法運算。其中FA是一位全加器，當M=0時，Bi與M的異或值就是M,所以全加器的輸入就是A和B,當M=1時，Bi與M異或就是對Bi取反，然後C0=M=1,所以整個運算就是對B取反加1，是不是很熟悉，對，，，就是在上文中補碼減法裡的[ - y ]補的求法，所以當M=1時，這個加法器執行的是A補 + [ - B ]補，即A-B的補碼減法運算，所以只要改變M的取值就可以操作是做加法還是減法了，最後要補充的是這個加法器判斷溢位方式是採取單符號位法，把最高數值位的進位和符號位的進位同時輸入到一個異或門進行異或運算，然後根據結果判斷是否溢位。先總結這麼多，，，，這樣再理解定點乘法應該要容易的多吧~~~~~