運用深度學習進行藝術風格轉換
使用深度學習進行藝術風格轉換始於 Leon Gatys 等人於2015年發表的論文 A Neural Algorithm of Artistic Style,為普通照片 “賦予” 名畫風格。由於其看上去不明覺厲的特性,在論文發表之後迅速得到了廣泛關注,此後幾年各種變種如雨後春筍般冒了出來,甚至誕生了大名鼎鼎的手機 app —— Prisma,下面就是一些通過 Prima 濾鏡生成的圖片。


本文主要參照這篇原始論文和書籍《Deep Learning with Python》對該項技術進行解讀和實現。
原理
藝術風格轉換的主要目的是將一張參考圖片的風格應用到另一張原始圖片上,最後的生成圖片能既保留原始圖片的大體內容,又展現出參考圖片的風格。在本文的語境中,風格 (style)
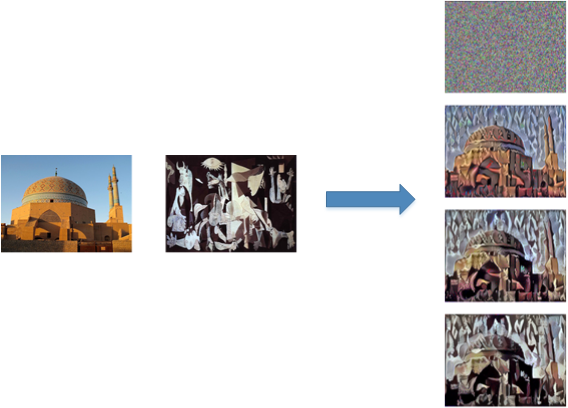
大致的流程是:輸入為白噪聲影象, 通過不斷修正輸入影象的畫素值來優化損失函式,最終得到的影象即輸出結果,如下圖:
在對這些概念明瞭了之後,接下來要做的事情就很常規了:定義一個損失函式,然後優化。損失函式大致長這樣:
\[ \large{loss = \underbrace{|參考圖片的風格 - 生成圖片的風格|}_{style \; loss}+ \underbrace{|原始圖片的內容 - 生成圖片的內容|}_{content \; loss}} \]
上式的意思是我們希望參考圖片與生成圖片的風格越接近越好,同時原始圖片與生成圖片的內容也越接近越好,這樣總體損失函式越小則最終的結果越好。當然光有這個式子是不行的,計算機只認數字不認其他,所以這裡的關鍵是如何用數學語言描述圖片的內容和風格?
Content Loss
上文提到圖片的內容主要指其巨集觀構造,而卷積神經網路的層數越深則越能提取圖片中全域性、抽象的資訊,因而論文中使用卷積神經網路中高層啟用函式的輸出來定義圖片的內容,那麼衡量目標圖片和生成圖片內容差異的指標就是其歐氏距離 (即 \(content \; loss\) ): \[ \mathcal{L}\,_{content}(C,G) = \frac12 \sum\limits_{i,j} (a^{[l](C)}_{ij} -a^{[l](G)}_{ij}) ^ 2 \]
其中 \(a^{[l]}_{ij}\) 表示第 \(l\) 層,第 \(i\) 個 \(feature \; map\) 的第 \(j\) 個輸出值。\((C)\) 表示原始圖片,\((G)\) 表示生成圖片,從上式可以看出比較的是二者在同一層啟用函式的輸出。
Style Loss
如何表示圖片的風格呢? “風格” 本來就是個比較飄渺的概念,所以沒有固定的表示方法,論文中採用的是同一隱藏層中不同 \(feature \; map\) 之間的 \(Gram\) 矩陣來表示風格,因而又稱為 “風格矩陣” 。
設 \(A\) 為 \(m \times n\) 的矩陣,則 \(n\) 階方陣 \(G\) 為 \(Gram\) 矩陣:
\[ G = A^TA = \begin{bmatrix} \bf{a}_1^T \\ \bf{a}_2^T \\ \vdots \\ \bf{a}_n^T \end{bmatrix} \begin{bmatrix} \bf{a}_1 \; \bf{a}_2 \; \cdots \;\bf{a}_n \end{bmatrix} = \begin{bmatrix} \bf{a}_1^T \bf{a}_1 & \bf{a}_1^T \bf{a}_2 & \cdots & \bf{a}_1^T\bf{a}_n \\ \bf{a}_2^T \bf{a}_1 & \bf{a}_2^T \bf{a}_2 & \cdots & \bf{a}_2^T\bf{a}_n \\ \vdots & \vdots & \ddots & \vdots \\ \bf{a}_n^T \bf{a}_1 & \bf{a}_n^T \bf{a}_2 & \cdots & \bf{a}_n^T\bf{a}_n \end{bmatrix} \]
對於同一個隱藏層來說,不同的 \(filter\) 會提取不同的特徵,假設有 \(N_l\) 個 \(filter\) ,每個 \(filter\) 輸出的 \(feature \; map\) 大小為 \(M_l\) (\(feature \; map\) 的 \(height \times width\)),則這個隱藏層的輸出可用一個矩陣 $A^l \in \mathbb{R}^{M_l \times N_l} $ 表示,則其 \(Gram\) 矩陣 \(G^l \in \mathbb{R}^{N_l \times N_l}\) 代表了不同 \(feature \; map\) 之間的相關性。 舉例來說,假設一個 \(filter\) 提取圖片的紅色特徵,另一個 \(filter\) 提取圖片的藍色特徵,如果 \(Gram\) 矩陣中這兩個特徵相關性高,則表示圖片中同時出現了紅色和藍色,這在某種程度上可以代表其 “風格”,如下圖:

在有了能定義風格的“風格矩陣”後,就能寫出單個隱藏層的 \(style \; loss\) 了: \[ \mathcal{L}^{[l]}_{style}(S, G) = \frac{1}{4 N_l^2 M_l^2} \sum\limits_{i,j} (G_{ij}^{[l](S)} - G_{ij}^{[l](G)})^2 \] 其中 \((S)\) 表示風格圖片,\((G)\) 表示生成圖片,\(G_{ij}\) 表示 \(Gram\) 矩陣。如果使用多個隱藏層,則總體 \(style \; loss\) 就是: \[ \mathcal{L}_{style}(S, G) = \sum\limits_l w^{[l]} \cdot \mathcal{L}^{[l]}_{style}(S, G) \] 其中 \(w^{[l]}\) 為各層的權重係數。
有了 \(content \; loss\) 和 \(style\;loss\) 後,總體 loss 就是其加權和: \[ \mathcal{L}_{total}(C,S,G) = \alpha \cdot \mathcal{L}\,_{content}(C,G) + \beta \cdot \mathcal{L}_{style}(S, G) \] \(\alpha\) 和 \(\beta\) 為超引數,用於調整 \(\mathcal{L}\,_{content}(C,G)\) 和 \(\mathcal{L}_{style}(S, G)\) 的相對比重。
實現
接下來我們來看論文中方法的具體實現,用的庫是 Keras。論文作者 Gatys 等人沒有從頭訓練一個CNN,而是使用了預訓練 (pre-trained) 的 VGG-19 網路來對圖片進行特徵提取,這些特徵可以幫助我們去衡量兩個影象的內容差異和風格差異。大致流程如下:
- 將參考圖片,原始圖片,生成圖片同時輸入 VGG-19 網路,計算各個隱藏層的輸出值。
- 定義並計算上文中描述的損失函式。
- 使用優化方法最小化損失函式。
首先讀取圖片,將所有圖片轉化為相似大小 (圖片的高統一為 400px)。
import numpy as np
from keras.applications import vgg19
from keras.preprocessing.image import load_img, img_to_array
target_image_path = "original.jpg"
style_reference_image_path = "style.jpg"
width, height = load_img(target_image_path).size
img_height = 400
img_width = int(width * img_height / height)
def preprocess_image(image_path): # 對圖片預處理
img = load_img(image_path, target_size=(img_height, img_width))
img = img_to_array(img)
img = np.expand_dims(img, axis=0)
img = vgg19.preprocess_input(img)
return img接下來匯入 VGG-19 網路,其輸入為三類圖片 (參考圖片,原始圖片和生成圖片) 的組合。
from keras import backend as K
target_image = K.constant(preprocess_image(target_image_path))
style_reference_image = K.constant(preprocess_image(style_reference_image_path))
combination_image = K.placeholder((1, img_height, img_width, 3))
input_tensor = K.concatenate([target_image,
style_reference_image,
combination_image], axis=0)
model = vgg19.VGG19(input_tensor=input_tensor, weights='imagenet', include_top=False)定義 \(content \;loss\) 和 \(style \; loss\) :
def content_loss(base, combination):
return K.sum(K.square(combination - base))
def gram_matrix(x): # 用於計算 gram matrix
#將表示深度的最後一維置換到前面,再flatten後就是上文中n*m的矩陣A
features = K.batch_flatten(K.permute_dimension(x, (2, 0, 1)))
gram = K.dot(features, K.transpose(features))
return gram
def style_loss(style, combination):
S = gram_matrix(style)
C = gram_matrix(combination)
channels = 3
size = img_height * img_width
return K.sum(K.square(S - C)) / (4. * (channels ** 2) * (size ** 2))下圖顯示了 VGG-19 的結構:

上文提到圖片的內容定義為卷積神經網路的高層啟用函式輸出,而風格則可以同時包含低層和高層輸出,於是可以用最上面第5個 block 的輸出計算 \(content \;loss\) ,所有5個 block 的輸出計算 \(style \; loss\) 。
model = vgg19.VGG19(input_tensor=input_tensor, weights='imagenet', include_top=False)
outputs_dict = dict([(layer.name, layer.output) for layer in model.layers]) # 各隱藏層名稱和輸出的對映
content_layer = 'block5_conv2' # 第5個block
style_layers = ['block1_conv1',
'block2_conv1',
'block3_conv1',
'block4_conv1',
'block5_conv1'] # 所有5個block
style_weight = 1.
content_weight = 0.025
loss = K.variable(0.)
layer_features = outputs_dict[content_layer]
target_image_features = layer_features[0, :, :, :]
combination_features = layer_features[2, :, :, :]
loss += content_weight * content_loss(target_image_features,
combination_features)
for layer_name in style_layers:
layer_features = outputs_dict[layer_name]
style_reference_features = layer_features[1, :, :, :]
combination_features = layer_features[2, :, :, :]
style = style_loss(style_reference_features, combination_features)
loss += (style_weight * (style / len(style_layers)))有了損失函式之後,最後一步就是優化。論文中使用的優化方法是 L-BFGS 演算法,屬於擬牛頓法之一,具有收斂速度快的特點。在這裡我們使用 SciPy 中的 L-BFGS 演算法,由於 Scipy 中的實現需要分別傳入計算損失和梯度的函式,而分別計算這兩個值會造成大量多餘計算,所以這裡建立一個 Evaluator 類,同時計算損失和梯度後由兩個方法 [loss() 和 grads()]分別獲得。
grads = K.gradients(loss, combination_image)[0]
fetch_loss_and_grads = K.function([combination_image], [loss, grads])
class Evaluator(object): # 建立一個類,同時計算loss和gradient
def __init__(self):
self.loss_value = None
self.grads_values = None
def loss(self, x):
assert self.loss_value is None
x = x.reshape((1, img_height, img_width, 3))
outs = fetch_loss_and_grads([x])
loss_value = outs[0]
grad_values = outs[1].flatten().astype('float64')
self.loss_value = loss_value
self.grad_values = grad_values
return self.loss_value
def grads(self, x):
assert self.loss_value is not None
grad_values = np.copy(self.grad_values)
self.loss_value = None
self.grad_values = None
return grad_values
evaluator = Evaluator()經過了上面的鋪墊後,就可以進行正式優化了,下面的程式碼迭代了20輪,並儲存每一輪生成的圖片。
from scipy.optimize import fmin_l_bfgs_b
from scipy.misc import imsave
import time
def deprocess_image(x): # 對生成的圖片進行後處理
x[:, :, 0] += 103.939
x[:, :, 1] += 116.779
x[:, :, 2] += 123.68
x = x[:, :, ::-1] # 'BGR'->'RGB'
x = np.clip(x, 0, 255).astype('uint8')
return x
result_prefix = 'style_transfer_result'
iterations = 20
x = preprocess_image(target_image_path)
x = x.flatten()
for i in range(1, iterations + 1):
print('start of iteration', i)
start_time = time.time()
x, min_val, info = fmin_l_bfgs_b(evaluator.loss, x,
fprime=evaluator.grads, maxfun=20)
print('Current loss value: ', min_val)
img = x.copy().reshape((img_height, img_width, 3))
img = deprocess_image(img)
fname = result_prefix + '_at_iteration_%d.png' % i
imsave(fname, img)
print('Image saved as', fname)
print('Iteration %d completed in %ds' % (i, time.time() - start_time))來看看效果:


上面的例子中風格參考圖片只用了一張,然而我們還可以使用多張圖片來產生一種混搭風格,方法就是對每張圖片的 \(Gram\) 矩陣作加權平均。具體實現是要在 \(style \; loss\) 的定義中加入權重:
def style_loss(style, combination, weight):
assert len(style) == len(weight) # 圖片數與權重數應相同
S = [gram_matrix(st) * w for st, w in zip(style, weight)]
S = K.sum(S, axis=0)
C = gram_matrix(combination)
channels = 3
size = img_height * img_width
return K.sum(K.square(S - C)) / (4. * (channels ** 2) * (size ** 2))
for layer_name in style_layers:
layer_features = outputs_dict[layer_name]
style_reference_features = layer_features[1, :, :, :]
style_reference_features_2 = layer_features[2, :, :, :]
combination_features = layer_features[3, :, :, :]
style = style_loss([style_reference_features, style_reference_features_2, style_reference_features_3], combination_features, [0.2, 0.4, 0.4])
loss += (style_weight * (style / len(style_layers)))


上面的 風格參考圖片1為蒙克的《吶喊》,風格參考圖片2為倫勃朗的《夜巡》,風格參考圖片3為死亡金屬專輯《Altar of Madness》的封面。其中《吶喊》被賦予的權重較低,所以其風格也少一些。
當然,這種風格轉換的技術也有侷限,其比較適合色調明亮,對比強烈的畫作,如野獸派、立體派、後印象派等等,而若使用一些看上去相對“清淡”的畫作為風格圖片,則效果不明顯。所以總的來說這種技術還是有很多探索空間的,下面以Github上的另一個實現作結:

完整程式碼
/
