在C/C++中float是32位的，double是64位的，兩者在記憶體中的儲存方式和能夠表示的精度均不同，目前C/C++編譯器標準都遵照IEEE制定的浮點數表示法來進行float,double運算。

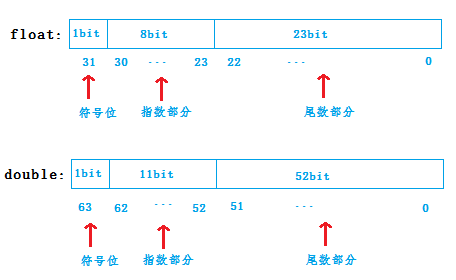
無論是float還是double，在記憶體中的儲存主要分成三部分，分別是：

（1）符號位（Sign）：0代表正數，1代表負數

（2）指數位（Exponent）：用於儲存科學計數法中的指數部分，並且採用移位儲存方式

（3）尾數位（Mantissa）：用於儲存尾數部分

對於兩者在記憶體中的儲存結構，如下圖所示：

    數字float 9.125在十進位制中用科學計算的方式表示為9.125*10^0  ，但是在計算機中，計算機只認識0和1，所以在計算機中是按照科學計算的二進位制的方式表示的：

9的二進位制表示為1001

0.125的二進位制表示為0.001

所以9.125的表示成1001.001  將其表示成二進位制的科學計數方式為 1.001001*2^3 

在計算機中，任何一個數都可以表示成1.xxxxxx*2^n 這樣的形式，

其中xxxxx就表示尾數部分，n表示指數部分

其中，因為最高位橙色的1這裡，由於任何的一個數表示成這種形式時這裡都是1，所以在儲存時實際上並不儲存這一位，這使得float的23bit的尾數可以表示24bit的精度，double中52bit的尾數可以表達53bit的精度。

    對於float型資料，可以精確到小數點後幾位呢？當然，學過c的同學會說float能夠精確到小數點後6位，但這是怎麼的來的呢？下面做一點解釋：

    十進位制中的9，在二進位制中的表示形式是1001，這裡也就告訴我們，表示十進位制中的一位數在二進位制中需要4bit，所以我們現在float中具有24bit的精度，所以float在十進位制中具有24/4=6，所以在十進位制裡，float能夠精確到小數點後6位。同理，具有53bit精度的double型別能夠精確到小數點後13位。

    對於float型別，他的指數部分有8bit，可以表示-127~128，但是這裡採用了移位儲存的方式（對這個概念不太清楚），在儲存指數時資料的基數是127，而不是0,。例如上面的9.125，其二進位制的指數部分為3，所以在儲存時實際上存的是127+3=130。（130的二進位制表示為10000010）

最終根據上面圖中float的儲存結構可以知道，實際上9.125在計算機中：

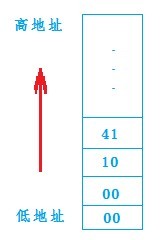
上面的二進位制數轉換成十六進位制後表示形式為：01000001 00010000 00000000 00000000 --> 41 10 00 00

實際上在X86計算機中，採用的是小端儲存方式，即低地址儲存低位資料，高地址儲存高位資料。

所以資料應該是這樣儲存的：

對於double型別的儲存方式實際上和float是類似的，只是儲存的位數不同，在原理上都是一樣的。