numpy中維度的正確理解姿勢
作者:千千Sama
原文地址:https://blog.csdn.net/lllxxq141592654/article/details/83011056
文章目錄
前言
在使用numpy的時候,有時候會遇到這樣的問題:
- 為什麼數學裡的向量在numpy中需要用兩個
[]括起來?如[[1 2 3]] - 維度為
(2,3,4)的矩陣是什麼鬼? - 什麼?還有維度為
(3,)的矩陣?
如果你有這樣的問題,說明對numpy中矩陣的準確表達不夠理解,下面就來為你排憂解難!
理解numpy矩陣維度的正確姿勢
我們線上性代數中最常見到的矩陣入手,就是類似這樣的了:
⎣⎡147⎦⎤
是一個3×1的矩陣,所以在numpy中的表達應該是
[[1 2 3]]
- 1
它的shape也即(3,1)
因為需要用兩個座標資訊索引某一元素,所以它的維數也為2
以上就是矩陣和向量在numpy中的正確表達。
我們已經把最常見的掌握好了,現在來探索一下更復雜的情況。
有人可能見過這樣的shape:(3,),也見過這樣的numpy表達[1,2,3](注意只有一對括號)。這是怎麼回事呢?
原來,如果我們沒有給numpy指定列資訊(也即第二維),那麼它的shape就是(3,),其實上面的[1,2,3]就是shape為(3,)的一個例子。
注意:形如[1,2,3]這樣的東西看似是個數學中的向量,其實並不是!不要下意識的認為它就是個向量,numpy是不這麼認的!
那它到底是什麼呢?它只是幾個數,用一個維度排列起來。
因為索引某個具體元素只需要一個座標資訊,所以
[1,2,3]的維數是1.
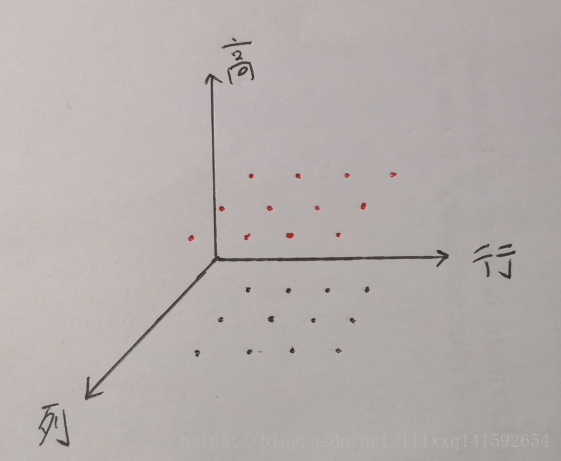
最後看維度為(2,3,4)的矩陣。
通過上面的講解,我們明白可以把維度類比為座標軸,那麼維度為(2,3,4)的矩陣就好理解了,一張圖即可
因為索引某個具體元素需要行,列,高,3個座標資訊,所以矩陣的維數是3,。
舉個具體例子
[[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[[13 14 15 16]
[17 18 19 20]
[21 22 23 24]]]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
關於矩陣的axis
矩陣的axis的規定是這樣的——維度中的第一個定義為axis=0,第二個axis=1,以此類推。
例如,維度為(1,3)的矩陣,它的axis有2個,第一個1代表的那個軸,第二個是3代表的那個軸
維度為(2,3,4)的矩陣,它的axis有3個,第一個2代表的那個軸,第二個是3代表的那個軸,第三個是4代表的那個軸。
我們用numpy.sum求和函式來做實驗
官網手冊的用法是
numpy.sum(a, axis=None, dtype=None, out=None, keepdims=<class numpy._globals._NoValue>)
- 1
這裡我們只看axis這個引數。
根據上面說的axis的含義,矩陣
[121518]
需要指定axis=0
import numpy as np
a=np.arange(1,10).reshape(3,3)
print(a)
print(np.sum(a,axis=0))
- 1
- 2
- 3
- 4
[[1 2 3]
[4 5 6]
[7 8 9]]
[12 15 18]
- 1
- 2
- 3
- 4
再舉個例子,矩陣
[[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[[13 14 15 16]
[17 18 19 20]
[21 22 23 24]]]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
若指定axis=0進行求和,結果應該是什麼樣的呢?
提示,想一下這張圖
它的axis=0的軸對應的是2代表的那個維度,也即圖中的高,沿著這個軸對矩陣進行求和,其實就是把兩個(3×4)的矩陣合併,那麼答案就很明顯了
import numpy as np
a=np.arange(1,25).reshape(2,3,4)
print(a)
print("--------------")
print(np.sum(a,axis=0))
- 1
- 2
- 3
- 4
- 5
[[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[[13 14 15 16]
[17 18 19 20]
[21 22 23 24]]]
--------------
[[14 16 18 20]
[22 24 26 28]
[30 32 34 36]]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
同理,axis=1,axis=2的時候答案是什麼呢?
axis=1
[[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[[13 14 15 16]
[17 18 19 20]
[21 22 23 24]]]
--------------
[[15 18 21 24]
[51 54 57 60]]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
axis=2
[[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[[13 14 15 16]
[17 18 19 20]
[21 22 23 24]]]
--------------
[[10 26 42]
[58 74 90]]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
寫在最後
關於axis的內容,其實在寫的時候留了個小陷阱——求和後維度貌似少了一維,比如3階矩陣,按行按列求和後是個向量,應該也是兩對[]呀,怎麼變成一個了?這就涉及到numpy的另一個引數了——keepdims。如果你不會用這個引數,請參見numpy中keepdims的理解