[poj1151]Atlantis & [poj1177]picture(掃描線)
【poj1151】
http://poj.org/problem?id=1151
題意:
在平面直角座標系上有一些矩形,他們可能會互相重疊,求矩陣的並(也就是所有矩陣覆蓋的部分)的面積。譬如說:
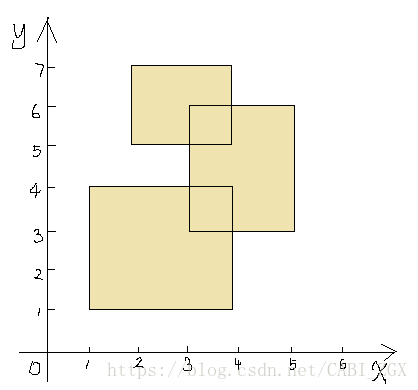
掃描線模板題。 離散y座標,以y座標建立線段樹跑掃描線。排序x,每次去差值乘上線段樹根節點所維護掃描線長度即算出面積進入答案中。 線上段樹中維護一個cnt和一個len,len表示當前線段樹節點所維護的掃描線長度,cnt表示當前線段樹所維護區間的重疊情況,輔助維護len(知道什麼時候更新)。進來一條線就給維護這條線的線段樹節點的cnt+1。向上更新的時候,當一個節點的cnt>0的時候就更新他的長度,否則他的長度等於他左右兒子的長度和。具體可以模擬一下過程。
注意掃描線的建樹和普通線段樹不同。掃描線的線段樹維護的是點,所以我們在分左右孩子建樹時的區間時(l,mid)和(mid,r)而不是像之前那樣打(mid+1,r)。如果打(mid+1,r)的會維護不到(mid,mid+1)的點。
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int MX=1e5+10;
const int N=3e2+10;
struct 【poj1177】Picture
http://poj.org/problem?id=1177
題意:
在平面直角座標系上有一些矩形,他們可能會互相重疊,求矩陣的並(也就是所有矩陣覆蓋的部分)的周長。譬如說:
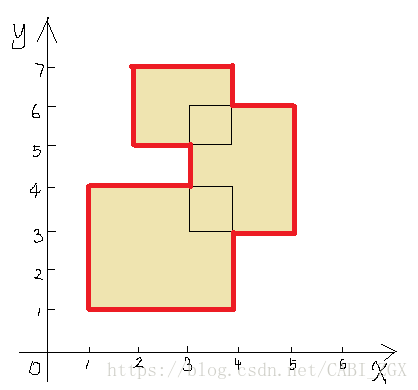
同樣離散化y座標建立線段樹跑掃描線,同時按照x排序。 我們發現對於豎線我們可以參照上一題的維護方法維護一個cnt和len,在每次進來一條新的豎線之後change進線段樹後給答案加上(abs(上次的答案 - 現在根節點所維護掃描線長度))即可。
但是對於橫線應該如何辦呢?我們考慮什麼時候要計算橫線,只有當兩條豎線分開的時候,中間才會拉出來橫線。那麼我們可以維護一個num,表示當前節點下的連續線段有多少個。也就是說,如果一個節點下面維護了(1,3),(4,5),(5,6)三條線段,那麼num=2,因為(4,5)(5,6)是連續的,他們兩個只會拉出來兩條橫線。 那麼為了維護他,我們在cnt的基礎上需要維護一個lp,rp表示線段的兩端有沒有被覆蓋. 噹噹前節點的cnt>0時,num=1,cnt如果左孩子的rp=1. 當前cnt=0時,當前節點的num=左右孩子的num和,但是如果右孩子的lp=1那就說明中間重複了,那麼當前節點的num就要-1。
維護了num就可以計算橫線的值了,每次進來一個掃描線,我們把橫座標和上一個作差得出這一段要加的幾條橫線的長度,然後根節點的num值*2(因為有上下兩條邊)就是當前要加的橫線的數量,乘起來計入答案即可。
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=1e4+10;
struct seg
{
double l,r;
int cnt,num;//num 線段樹中連續的線段有多少條
double len;
int lp,rp;//lp rp記錄這一個節點的兩個端點是不是已經覆蓋 來維護num
}tr[N*4];
int n;
struct node
{
double x,y1,y2;
int flag;
}p[N*2];
bool cmp(node a,node b){return a.x<b.x;}
double b[N*2];
void push_up(int now)
{
if(tr[now].cnt>0)
{
tr[now].lp=tr[now].rp=1;
tr[now].num=1;
tr[now].len=tr[now].r-tr[now].l;
}
else
{
int lc=now*2,rc=now*2+1;
tr[now].len=tr[lc].len+tr[rc].len;
tr[now].num=tr[lc].num+tr[rc].num;
tr[now].lp=tr[lc].lp; tr[now].rp=tr[rc].rp;
if(tr[lc].rp && tr[rc].lp) tr[now].num--;
//debug 如果左節點的rp與右節點的lp都是1,那麼父節點的num值減去1
}
}
void build(int now,int l,int r)
{
tr[now].l=b[l]; tr[now].r=b[r];
tr[now].lp=tr[now].rp=0;
if(l>=r-1){tr[now].num=tr[now].len=tr[now].cnt=0; return;}
if(l<r+1)
{
int mid=(l+r)/2,lc=now*2,rc=now*2+1;
build(lc,l,mid);
build(rc,mid,r);
push_up(now);
}
}
void change(int now,double y1,double y2,int p)
{
if(tr[now].l==y1 && tr[now].r==y2)
{
tr[now].cnt+=p;
push_up(now);
return;
}
int lc=now*2,rc=now*2+1;
if(tr[lc].r>y1)
change(lc,y1,min(tr[lc].r,y2),p);
if(tr[rc].l<y2)// debug 不打else 兩個都可以進行
change(rc,max(tr[rc].l,y1),y2,p);
push_up(now);
}
int main()
{
int n;
while(~scanf("%d",&n))
{
double x1,y1,x2,y2;
memset(b,0,sizeof(b));
for(int i=1;i<=n;i++)
{
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
p[i].x=x1; p[i].y1=y1; p[i].y2=y2; p[i].flag=1;
p[i+n].x=x2; p[i+n].y1=y1; p[i+n].y2=y2; p[i+n].flag=-1;
b[i]=y1; b[i+n]=y2;
}
sort(b+1,b+2*n+1);
int m=unique(b+1,b+2*n+1)-(b+1);
build(1,1,m);
sort(p+1,p+2*n+1,cmp);
double ans=0,last=0;
change(1,p[1].y1,p[1].y2,p[1].flag);
ans+=fabs(last-tr[1].len);
last=tr[1].len;
for(int i=2;i<=2*n;i++)
{
ans+=(p[i].x-p[i-1].x)*tr[1].num*2;//橫線
change(1,p[i].y1,p[i].y2,p[i].flag);
ans+=fabs(last-tr[1].len); //豎線
last=tr[1].len;
}
printf("%.0lf\n",ans);
}
return 0;
}
