P0 前言

• 第二門課 : Improving Deep Neural Networks: Hyperparameter turing,Regularization and Optimization (改善深層神經網路：超引數除錯、正則化以及優化)
• 第二週 : Hyperparameter Tuning (超引數除錯和Batch Norm及框架)
• 主要知識點 : 超引數的除錯、Batch Normalization、Softmax、TensorFlow程式框架等；

視訊地址：https://mooc.study.163.com/learn/2001281003?tid=2001391036#/learn/announce

筆記地址：以後補

資料集，原始碼，作業的本地版網頁快取下載：連結：https://pan.baidu.com/s/1Mbj9jlxlx591Rag-zLiHPQ  提取碼：q9aa

                                                   P1 作業

之前都是使用Numpy來搭建神經網路，這周開始用深度學習框架（tensorflow）來構建網路模型。

1-探索Tensorflow的library

首先匯入需要的包

import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.python.framework import ops
from tf_utils import load_dataset, random_mini_batches, convert_to_one_hot, predict
​
%matplotlib inline
np.random.seed(1)
 

一些有用的函式（在tf_utils.py中）：

def load_dataset():
    train_dataset = h5py.File('datasets/train_signs.h5', "r")
    train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
    train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels

    test_dataset = h5py.File('datasets/test_signs.h5', "r")
    test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
    test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels

    classes = np.array(test_dataset["list_classes"][:]) # the list of classes

    train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
    test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))

    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes


def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
    """
    Creates a list of random minibatches from (X, Y)

    Arguments:
    X -- input data, of shape (input size, number of examples)
    Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
    mini_batch_size - size of the mini-batches, integer
    seed -- this is only for the purpose of grading, so that you're "random minibatches are the same as ours.

    Returns:
    mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
    """

    m = X.shape[1]                  # number of training examples
    mini_batches = []
    np.random.seed(seed)

    # Step 1: Shuffle (X, Y)
    permutation = list(np.random.permutation(m))
    shuffled_X = X[:, permutation]
    shuffled_Y = Y[:, permutation].reshape((Y.shape[0],m))

    # Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
    num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
    for k in range(0, num_complete_minibatches):
        mini_batch_X = shuffled_X[:, k * mini_batch_size : k * mini_batch_size + mini_batch_size]
        mini_batch_Y = shuffled_Y[:, k * mini_batch_size : k * mini_batch_size + mini_batch_size]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    # Handling the end case (last mini-batch < mini_batch_size)
    if m % mini_batch_size != 0:
        mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size : m]
        mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size : m]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    return mini_batches


def convert_to_one_hot(Y, C):
    Y = np.eye(C)[Y.reshape(-1)].T
    return Y


def predict(X, parameters):

    W1 = tf.convert_to_tensor(parameters["W1"])
    b1 = tf.convert_to_tensor(parameters["b1"])
    W2 = tf.convert_to_tensor(parameters["W2"])
    b2 = tf.convert_to_tensor(parameters["b2"])
    W3 = tf.convert_to_tensor(parameters["W3"])
    b3 = tf.convert_to_tensor(parameters["b3"])

    params = {"W1": W1,
              "b1": b1,
              "W2": W2,
              "b2": b2,
              "W3": W3,
              "b3": b3}

    x = tf.placeholder("float", [12288, 1])

    z3 = forward_propagation_for_predict(x, params)
    p = tf.argmax(z3)

    sess = tf.Session()
    prediction = sess.run(p, feed_dict = {x: X})

    return prediction

先來個開胃菜，實現這個函式： 

如下所示（已經為你實現好了）：

y_hat = tf.constant(36, name='y_hat')            # Define y_hat constant. Set to 36.
y = tf.constant(39, name='y')                    # Define y. Set to 39

loss = tf.Variable((y - y_hat)**2, name='loss')  # Create a variable for the loss

init = tf.global_variables_initializer()         # When init is run later (session.run(init)),
                                                 # the loss variable will be initialized and ready to be computed
with tf.Session() as session:                    # Create a session and print the output
    session.run(init)                            # Initializes the variables
    print(session.run(loss))                     # Prints the loss

#下面是輸出結果
9

由此可見用tensorflow寫程式需要以下幾步：

• 建立（尚未執行/計算的）張量(變數，variable)。
• 在這些張量之間定義運算。
• 初始化你的張量。
• 建立一個會話（session）。
• 執行會話。這將執行您上面所寫的操作。

注意到前兩行我們只是定義了張量，一直到第四行才初始化他們。同理，第三行我們也只是定義了運算，到了第五行我們才使用session來進行實際的計算。

再看一個例子：

a = tf.constant(2)
b = tf.constant(10)
c = tf.multiply(a,b)
print(c)

#執行結果
Tensor("Mul:0", shape=(), dtype=int32)

正如預料中一樣，我們並沒有看到結果20，不過我們得到了一個Tensor型別的變數，沒有維度，數字型別為int32。我們之前所做的一切都只是把這些東西放到了一個“計算圖(computation graph)”中，而我們還沒有開始執行這個計算圖，為了實際計算這兩個數字，我們需要建立一個會話並執行它：
 

sess = tf.Session()
print(sess.run(c))

#執行結果
20

總結：

• 定義的變數都需要初始化
• 定義的運算需要session來執行

下面再來了解一下佔位符（placeholders）。

佔位符是一個物件，它的值只能在稍後指定，要指定佔位符的值，可以使用一個feed字典（feed_dict變數）來傳入，接下來，我們為x建立一個佔位符，這將允許我們在稍後執行session時傳入一個數字。

# Change the value of x in the feed_dict
​
x = tf.placeholder(tf.int64, name = 'x')
print(sess.run(2 * x, feed_dict = {x: 3}))
sess.close()

當我們第一次定義x時，我們不必為它指定一個值。 佔位符只是一個變數，我們會在執行會話時將資料分配給它。

1.1 線性函式

實現Y=WX+b的tf版本（其中W和X是隨機矩陣，b是隨機向量，W維度（4,3）X維度（3,1）b維度（4,1））

提示：定義一個（3,1）的X可以像這樣：

X = tf.constant(np.random.randn(3,1), name = "X")

你可能用到的函式：

# GRADED FUNCTION: linear_function

def linear_function():
    """
    Implements a linear function:
            Initializes W to be a random tensor of shape (4,3)
            Initializes X to be a random tensor of shape (3,1)
            Initializes b to be a random tensor of shape (4,1)
    Returns:
    result -- runs the session for Y = WX + b
    """

    np.random.seed(1)

    ### START CODE HERE ### (4 lines of code)
    X = np.random.randn(3,1)
    W = np.random.randn(4,3)
    b = np.random.randn(4,1)
    Y = tf.add(tf.matmul(W,X),b) #剛開始用的np.dot()習慣還是沒改過來，後來又用了tf.multiply()元素乘法導致維度錯
    ### END CODE HERE ###

    # Create the session using tf.Session() and run it with sess.run(...) on the variable you want to calculate

    ### START CODE HERE ###
    sess = tf.Session()
    result = sess.run(Y)#剛開始沒有在run裡給出要執行的運算
    ### END CODE HERE ###

    # close the session
    sess.close()

    return result

結果：

print("result = " +  str(linear_function()))

#結果如下
result = [[-2.15657382]
 [ 2.95891446]
 [-1.08926781]
 [-0.84538042]]

1.2 - 計算sigmoid

其實tensorflow已經為你實現了一些特殊的函式如：tf.sigmoid,tf.softmax等，但是實際使用中很少有直接向tf.sigmoid傳實值的，一般需要用到placeholder，本節的目的就是用佔位符和tf.sigmoid實現一個可用的sigmoid模組介面API。

你可能用到的函式：

# GRADED FUNCTION: sigmoid​
def sigmoid(z):
    """
    Computes the sigmoid of z

    Arguments:
    z -- input value, scalar or vector

    Returns:
    results -- the sigmoid of z
    """

    ### START CODE HERE ### ( approx. 4 lines of code)
    # Create a placeholder for x. Name it 'x'.
    x = tf.placeholder(tf.float32,name="x")#剛開始沒寫引數TypeError: placeholder() missing 1 required positional argument: 'dtype'
    #忽略第二個引數也能執行

    # compute sigmoid(x)
    sigmoid = tf.sigmoid(x)

    # Create a session, and run it. Please use the method 2 explained above.
    # You should use a feed_dict to pass z's value to x.
    sess = tf.Session()
    # Run session and call the output "result"
    result = sess.run(sigmoid,feed_dict={x:z})#可見函式的傳入引數z直到seesrun階段才被用上

    ### END CODE HERE ###

    return result

結果如下：

print ("sigmoid(0) = " + str(sigmoid(0)))
print ("sigmoid(12) = " + str(sigmoid(12)))

#結果：
sigmoid(0) = 0.5
sigmoid(12) = 0.999994

1.3 - 計算成本

回顧一下之前使用numpy計算cost的方式：

# GRADED FUNCTION: compute_cost
 
def compute_cost(AL, Y):
    """
    Implement the cost function defined by equation (7).
    Arguments:
    AL -- probability vector corresponding to your label predictions, shape (1, number of examples)
    Y -- true "label" vector (for example: containing 0 if non-cat, 1 if cat), shape (1, number of examples)
    Returns:
    cost -- cross-entropy cost
    """
 
    m = Y.shape[1]
 
    # Compute loss from aL and y.
    ### START CODE HERE ### (≈ 1 lines of code)
    cost = -np.sum(np.multiply(np.log(AL),Y) + np.multiply(np.log(1 - AL), 1 - Y)) / m
    ### END CODE HERE ###
 
    cost = np.squeeze(cost)      # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).
    assert(cost.shape == ())
 
    return cost

在tensorflow中使用一個函式  ：tf.nn.sigmoid_cross_entropy_with_logits(logits = ..., labels = ...)就能實現上述運算，如下所示：

# GRADED FUNCTION: cost

def cost(logits, labels):
    """
    Computes the cost using the sigmoid cross entropy

    Arguments:
    logits -- vector containing z, output of the last linear unit (before the final sigmoid activation)
    labels -- vector of labels y (1 or 0)

    Note: What we've been calling "z" and "y" in this class are respectively called "logits" and "labels"
    in the TensorFlow documentation. So logits will feed into z, and labels into y.

    Returns:
    cost -- runs the session of the cost (formula (2))
    """

    ### START CODE HERE ###

    # Create the placeholders for "logits" (z) and "labels" (y) (approx. 2 lines)
    z = tf.placeholder(dtype=tf.float32,name="z")
    y = tf.placeholder(dtype=tf.float32,name="y")

    # Use the loss function (approx. 1 line)
    cost = tf.nn.sigmoid_cross_entropy_with_logits(logits=z,labels=y)#logits是最後一層啟用層的輸出值

    # Create a session (approx. 1 line). See method 1 above.
    sess = tf.Session()

    # Run the session (approx. 1 line).
    cost = sess.run(cost,feed_dict={z:logits,y:labels})

    # Close the session (approx. 1 line). See method 1 above.
    sess.close()

    ### END CODE HERE ###

    return cost

結果：

logits = sigmoid(np.array([0.2, 0.4, 0.7, 0.9]))
cost = cost(logits, np.array([0, 0, 1, 1]))
print("cost = " + str(cost))

#結果
cost = [1.0053872  1.0366409  0.4138543  0.39956614]

1.4 - 使用獨熱編碼（0、1編碼）

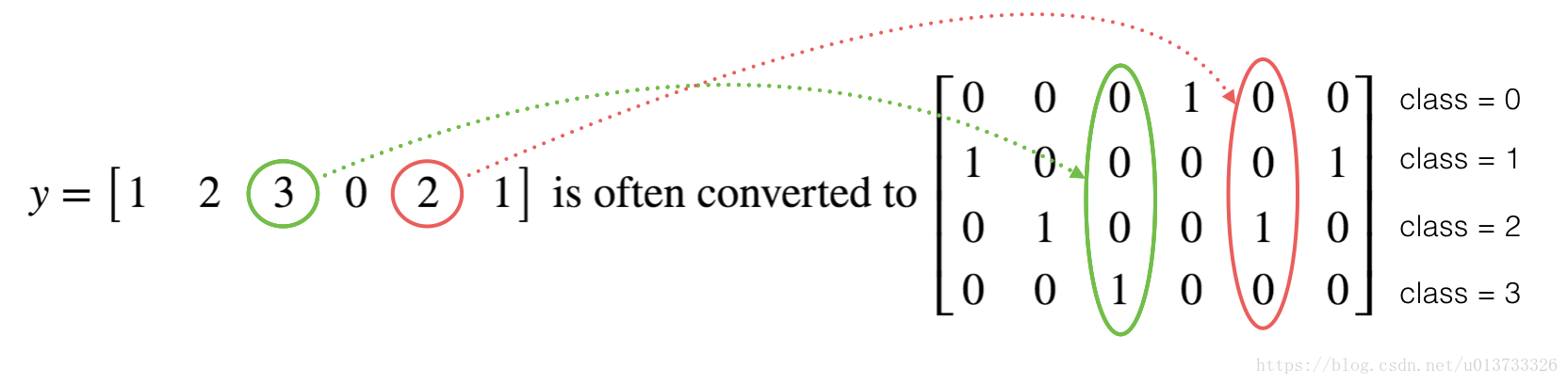
深度學習中label一般來說要轉換成獨熱碼作為輸入，如下所示：

 在tensorflow中，只需要使用一行程式碼就能實現（numpy則複雜一點）：tf.one_hot(labels, depth, axis)

注意axis的含義（見程式碼），axis預設為1，也就是以列號為類號

# GRADED FUNCTION: one_hot_matrix

def one_hot_matrix(labels, C):
    """
    Creates a matrix where the i-th row corresponds to the ith class number and the jth column
                     corresponds to the jth training example. So if example j had a label i. Then entry (i,j)
                     will be 1.

    Arguments:
    labels -- vector containing the labels
    C -- number of classes, the depth of the one hot dimension

    Returns:
    one_hot -- one hot matrix
    """

    ### START CODE HERE ###

    # Create a tf.constant equal to C (depth), name it 'C'. (approx. 1 line)
    C = tf.constant(C,name="C")

    # Use tf.one_hot, be careful with the axis (approx. 1 line)
    one_hot_matrix = tf.one_hot(labels,C,axis=0)#剛開始沒加axis結果錯誤是個6*4矩陣,axis=0代表以行號為類號,=1是列號為類號

    # Create the session (approx. 1 line)
    sess = tf.Session()

    # Run the session (approx. 1 line)
    one_hot = sess.run(one_hot_matrix) #C現在是tfconstant不用feeddic

    # Close the session (approx. 1 line). See method 1 above.
    sess.close()

    ### END CODE HERE ###

    return one_hot

結果：

labels = np.array([1, 2, 3, 0, 2, 1])
one_hot = one_hot_matrix(labels, C=4)
print("one_hot = " + str(one_hot))

#結果：
one_hot = [[0. 0. 0. 1. 0. 0.]
 [1. 0. 0. 0. 0. 1.]
 [0. 1. 0. 0. 1. 0.]
 [0. 0. 1. 0. 0. 0.]]

1.5 - 初始化為0和1

現在我們將學習如何用0或者1初始化一個向量，我們要用到tf.ones()和tf.zeros()，給定這些函式一個維度值那麼它們將會返回全是1或0的滿足條件的向量/矩陣，我們來看看怎樣實現它們：

# GRADED FUNCTION: ones

def ones(shape):
    """
    Creates an array of ones of dimension shape

    Arguments:
    shape -- shape of the array you want to create

    Returns:
    ones -- array containing only ones
    """

    ### START CODE HERE ###

    # Create "ones" tensor using tf.ones(...). (approx. 1 line)
    ones = tf.ones(shape)

    # Create the session (approx. 1 line)
    sess = tf.Session()

    # Run the session to compute 'ones' (approx. 1 line)
    ones = sess.run(ones)

    # Close the session (approx. 1 line). See method 1 above.
    sess.close()

    ### END CODE HERE ###
    return ones


#檢視結果：
print("ones = " + str(ones([3])))
#結果：
ones = [1. 1. 1.]

2 - 使用TensorFlow構建你的第一個神經網路

我們將會使用TensorFlow構建一個神經網路，需要記住的是實現模型需要做以下兩個步驟： 
1. 建立計算圖 
2. 執行計算圖

我們開始一步步地走一下：

2.0 - 要解決的問題

建立一個演算法進行手勢識別。下面是每個數字的樣本，以及我們如何表示標籤的解釋。這些都是原始圖片，我們實際上用的是64 * 64畫素的圖片。 

• 訓練集：有從0到5的數字的1080張圖片(64x64畫素)，每個數字擁有180張圖片。
• 測試集：有從0到5的數字的120張圖片(64x64畫素)，每個數字擁有5張圖片。

載入資料集：

# Loading the dataset
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()
index = 11
plt.imshow(X_train_orig[index])
print("Y = " + str(np.squeeze(Y_train_orig[:,index])))

#結果
Y = 1

 和往常一樣，我們要對資料集進行扁平化，然後再除以255以歸一化資料，除此之外，我們要需要把每個標籤轉化為獨熱向量，像上面的圖一樣。

    #扁平化
    X_train_flatten = X_train_orig.reshape(X_train_orig.shape[0], -1).T  # 每一列就是一個樣本
    X_test_flatten = X_test_orig.reshape(X_test_orig.shape[0], -1).T

    # 歸一化資料
    X_train = X_train_flatten / 255
    X_test = X_test_flatten / 255

    # 轉換為獨熱矩陣
    Y_train = convert_to_one_hot(Y_train_orig, 6)
    Y_test = convert_to_one_hot(Y_test_orig, 6)

    print("訓練集樣本數 = " + str(X_train.shape[1]))
    print("測試集樣本數 = " + str(X_test.shape[1]))
    print("X_train.shape: " + str(X_train.shape))
    print("Y_train.shape: " + str(Y_train.shape))
    print("X_test.shape: " + str(X_test.shape))
    print("Y_test.shape: " + str(Y_test.shape))


#結果
訓練集樣本數 = 1080
測試集樣本數 = 120
X_train.shape: (12288, 1080)
Y_train.shape: (6, 1080)
X_test.shape: (12288, 120)
Y_test.shape: (6, 120)

 我們的目標是構建能夠高準確度識別符號的演算法。 要做到這一點，你要建立一個TensorFlow模型，這個模型幾乎和你之前在貓識別中使用的numpy一樣（但現在使用softmax輸出）。要將您的numpy實現與tensorflow實現進行比較的話這是一個很好的機會。

  目前的模型是：LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SOFTMAX，SIGMOID輸出層已經轉換為SOFTMAX。當有兩個以上的類時，一個SOFTMAX層將SIGMOID一般化。

2.1 - 建立placeholders

我們的第一項任務是為X和Y建立佔位符，這將允許我們稍後在執行session時傳遞您的訓練資料。

# GRADED FUNCTION: create_placeholders

def create_placeholders(n_x, n_y):
    """
    Creates the placeholders for the tensorflow session.

    Arguments:
    n_x -- scalar, size of an image vector (num_px * num_px = 64 * 64 * 3 = 12288)
    n_y -- scalar, number of classes (from 0 to 5, so -> 6)

    Returns:
    X -- placeholder for the data input, of shape [n_x, None] and dtype "float"
    Y -- placeholder for the input labels, of shape [n_y, None] and dtype "float"

    Tips:
    - You will use None because it let's us be flexible on the number of examples you will for the placeholders.
      In fact, the number of examples during test/train is different.
    """


    ### START CODE HERE ### (approx. 2 lines)
    X = tf.placeholder(dtype=tf.float32,shape=[n_x,None],name="X")#剛開始直接用的float32報錯，因該是tf.float32
    Y = tf.placeholder(dtype=tf.float32,shape=[n_y,None],name="Y")
    ### END CODE HERE ###

    return X, Y

#檢視結果
X, Y = create_placeholders(12288, 6)
print("X = " + str(X))
print("Y = " + str(Y))

#結果
X = Tensor("X:0", shape=(12288, ?), dtype=float32)
Y = Tensor("Y:0", shape=(6, ?), dtype=float32)

2.2 - 初始化引數

初始化tensorflow中的引數，我們將使用Xavier初始化權重和用零來初始化偏差，比如：

W1 = tf.get_variable("W1", [25,12288], initializer = tf.contrib.layers.xavier_initializer(seed = 1))
b1 = tf.get_variable("b1", [25,1], initializer = tf.zeros_initializer())

注意：tf.Variable() 每次都在建立新物件，對於get_variable()來說，對於已經建立的變數物件，就把那個物件返回，如果沒有建立變數物件的話，就建立一個新的。

def initialize_parameters():
    """
    Initializes parameters to build a neural network with tensorflow. The shapes are:
                        W1 : [25, 12288]
                        b1 : [25, 1]
                        W2 : [12, 25]
                        b2 : [12, 1]
                        W3 : [6, 12]
                        b3 : [6, 1]

    Returns:
    parameters -- a dictionary of tensors containing W1, b1, W2, b2, W3, b3
    """

    tf.set_random_seed(1)  # so that your "random" numbers match ours

    ### START CODE HERE ### (approx. 6 lines of code)
    W1 = tf.get_variable(name="W1",shape=[25,12288],dtype=tf.float32,initializer=tf.contrib.layers.xavier_initializer(seed=1))
    b1 = tf.get_variable(name="b1",shape=[25,1],dtype=tf.float32,initializer=tf.zeros_initializer())
    W2 = tf.get_variable(name="W2",shape=[12,25],dtype=tf.float32,initializer=tf.contrib.layers.xavier_initializer(seed=1))
    b2 = tf.get_variable(name="b2",shape=[12,1],dtype=tf.float32,initializer=tf.zeros_initializer())
    W3 = tf.get_variable(name="W3",shape=[6,12],dtype=tf.float32,initializer=tf.contrib.layers.xavier_initializer(seed=1))
    b3 = tf.get_variable(name="b3",shape=[6,1],dtype=tf.float32,initializer=tf.zeros_initializer())
    ### END CODE HERE ###


    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2,
                  "W3": W3,
                  "b3": b3}

    return parameters

#檢視結果
tf.reset_default_graph()
with tf.Session() as sess:
    parameters = initialize_parameters()
    print("W1 = " + str(parameters["W1"]))
    print("b1 = " + str(parameters["b1"]))
    print("W2 = " + str(parameters["W2"]))
    print("b2 = " + str(parameters["b2"]))

#結果
W1 = <tf.Variable 'W1:0' shape=(25, 12288) dtype=float32_ref>
b1 = <tf.Variable 'b1:0' shape=(25, 1) dtype=float32_ref>
W2 = <tf.Variable 'W2:0' shape=(12, 25) dtype=float32_ref>
b2 = <tf.Variable 'b2:0' shape=(12, 1) dtype=float32_ref>

正如預期的那樣，這些引數只有物理空間，但是還沒有被賦值，這是因為沒有通過session執行。

2.3 - 前向傳播

我們將要在TensorFlow中實現前向傳播，該函式將接受一個字典引數並完成前向傳播，它會用到以下程式碼：

• tf.add(...,...) to do an addition
• tf.matmul(...,...) to do a matrix multiplication
• tf.nn.relu(...) to apply the ReLU activation

我們要實現神經網路的前向傳播，我們會拿numpy與TensorFlow實現的神經網路的程式碼作比較。兩者之間的重要區別是TF的前向傳播要在Z3處停止，因為在TensorFlow中最後的線性輸出層的輸出（Z3）作為計算損失函式（Cost_Function）的輸入，所以不需要A3.

# GRADED FUNCTION: forward_propagation

def forward_propagation(X, parameters):
    """
    Implements the forward propagation for the model: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SOFTMAX

    Arguments:
    X -- input dataset placeholder, of shape (input size, number of examples)
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3"
                  the shapes are given in initialize_parameters
​
    Returns:
    Z3 -- the output of the last LINEAR unit
    """

    # Retrieve the parameters from the dictionary "parameters"
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']
    W3 = parameters['W3']
    b3 = parameters['b3']

    ### START CODE HERE ### (approx. 5 lines)              # Numpy Equivalents:
    Z1 = tf.add(tf.matmul(W1,X),b1)  # Z1 = np.dot(W1, X) + b1
    A1 = tf.nn.relu(Z1)  # A1 = relu(Z1)
    Z2 = tf.add(tf.matmul(W2,A1),b2)  # Z2 = np.dot(W2, a1) + b2
    A2 = tf.nn.relu(Z2)  # A2 = relu(Z2)
    Z3 = tf.add(tf.matmul(W3,A2),b3)  # Z3 = np.dot(W3,A2) + b3
    ### END CODE HERE ###

    return Z3

#檢視結果
    tf.reset_default_graph()
    with tf.Session() as sess:
        X, Y = create_placeholders(12288, 6)
        parameters = initialize_parameters()
        Z3 = forward_propagation(X, parameters)
        print("Z3 = " + str(Z3))
#結果
Z3 = Tensor("Add_2:0", shape=(6, ?), dtype=float32)

您可能已經注意到前向傳播不會輸出任何cache，當我們完成反向傳播的時候你就會明白了。

2.4 - 計算成本

如前所述，成本很容易計算：

tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = ..., labels = ...))

由於Z3的維度是[N_3 , number of examples]，label的維度是[num_classes, number of examples],因此在計算cost前需要進行轉置（transpose）。此外tf.reduce_mean 是對所有樣本的求和。

# GRADED FUNCTION: compute_cost

def compute_cost(Z3, Y):
    """
    Computes the cost

    Arguments:
    Z3 -- output of forward propagation (output of the last LINEAR unit), of shape (6, number of examples)
    Y -- "true" labels vector placeholder, same shape as Z3

    Returns:
    cost - Tensor of the cost function
    """

    # to fit the tensorflow requirement for tf.nn.softmax_cross_entropy_with_logits(...,...)
    logits = tf.transpose(Z3)
    labels = tf.transpose(Y)

    ### START CODE HERE ### (1 line of code)
    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits,labels=labels))
    ### END CODE HERE ###

    return cost

#檢視結果
    tf.reset_default_graph()
    with tf.Session() as sess:
        X, Y = create_placeholders(12288, 6)
        parameters = initialize_parameters()
        Z3 = forward_propagation(X, parameters)
        cost = compute_cost(Z3, Y)
        print("cost = " + str(cost))
#結果
cost = Tensor("Mean:0", shape=(), dtype=float32)

2.5 - 反向傳播&更新引數

得益於程式設計框架，所有反向傳播和引數更新都在1行程式碼中處理。計算成本函式cost後，你將建立一個“optimizer”物件。執行tf.session時，必須將optimizer物件與成本函式cost一起呼叫（sess.run），當被呼叫時，它將使用所選擇的方法和學習速率對給定成本進行優化。

舉個例子，對於梯度下降:

optimizer = tf.train.GradientDescentOptimizer(learning_rate = learning_rate).minimize(cost)

要進行優化，應該這樣做：

_ , c = sess.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})

編寫程式碼時，我們經常使用 _ 作為一次性變數來儲存我們稍後不需要使用的值。 這裡，_具有我們不需要的optimizer的評估值（c則是cost的值）。

2.6 - 構建模型

def model(X_train, Y_train, X_test, Y_test, learning_rate=0.0001,
          num_epochs=1500, minibatch_size=32, print_cost=True):
    """
    Implements a three-layer tensorflow neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SOFTMAX.

    Arguments:
    X_train -- training set, of shape (input size = 12288, number of training examples = 1080)
    Y_train -- test set, of shape (output size = 6, number of training examples = 1080)
    X_test -- training set, of shape (input size = 12288, number of training examples = 120)
    Y_test -- test set, of shape (output size = 6, number of test examples = 120)
    learning_rate -- learning rate of the optimization
    num_epochs -- number of epochs of the optimization loop
    minibatch_size -- size of a minibatch
    print_cost -- True to print the cost every 100 epochs

    Returns:
    parameters -- parameters learnt by the model. They can then be used to predict.
    """

    ops.reset_default_graph()  # to be able to rerun the model without overwriting tf variables
    tf.set_random_seed(1)  # to keep consistent results
    seed = 3  # to keep consistent results
    (n_x, m) = X_train.shape  # (n_x: input size, m : number of examples in the train set)
    n_y = Y_train.shape[0]  # n_y : output size
    costs = []  # To keep track of the cost

    # Create Placeholders of shape (n_x, n_y)
    ### START CODE HERE ### (1 line)
    X, Y = create_placeholders(n_x=n_x,n_y=n_y)
    ### END CODE HERE ###


    # Initialize parameters
    ### START CODE HERE ### (1 line)
    parameters = initialize_parameters()
    ### END CODE HERE ###

    # Forward propagation: Build the forward propagation in the tensorflow graph
    ### START CODE HERE ### (1 line)
    Z3 = forward_propagation(X=X,parameters=parameters)
    ### END CODE HERE ###

    # Cost function: Add cost function to tensorflow graph
    ### START CODE HERE ### (1 line)
    cost = compute_cost(Z3=Z3,Y=Y)
    ### END CODE HERE ###

    # Backpropagation: Define the tensorflow optimizer. Use an AdamOptimizer.
    ### START CODE HERE ### (1 line)
    optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)#剛開始沒有minimize
    ### END CODE HERE ###

    # Initialize all the variables
    init = tf.global_variables_initializer()

    # Start the session to compute the tensorflow graph
    with tf.Session() as sess:
        # Run the initialization
        sess.run(init)

        # Do the training loop
        for epoch in range(num_epochs):

            epoch_cost = 0.  # Defines a cost related to an epoch
            num_minibatches = int(m / minibatch_size)  # number of minibatches of size minibatch_size in the train set
            seed = seed + 1
            minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)

            for minibatch in minibatches:

                #Select a minibatch
                (minibatch_X, minibatch_Y) = minibatch

                # IMPORTANT: The line that runs the graph on a minibatch.
                # Run the session to execute the "optimizer" and the "cost", the feedict should contain a minibatch for (X,Y).
                ### START CODE HERE ### (1 line)
                _, minibatch_cost = sess.run([optimizer,cost],feed_dict={X:minibatch_X,Y:minibatch_Y})
                ### END CODE HERE ###

                epoch_cost += minibatch_cost / num_minibatches

            # Print the cost every epoch
            if print_cost == True and epoch % 100 == 0:
                print("Cost after epoch %i: %f" % (epoch, epoch_cost))
            if print_cost == True and epoch % 5 == 0:
                costs.append(epoch_cost)

        # plot the cost
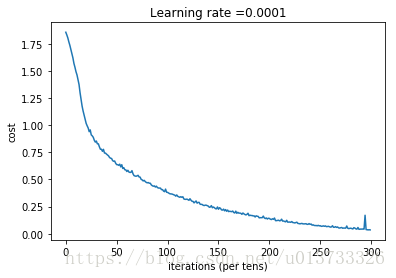
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()

        # lets save the parameters in a variable
        parameters = sess.run(parameters)#這句幹嘛的？？為什麼用run來儲存？
        print("Parameters have been trained!")

        # Calculate the correct predictions
        correct_prediction = tf.equal(tf.argmax(Z3), tf.argmax(Y))

        # Calculate accuracy on the test set
        accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))

        print("Train Accuracy:", accuracy.eval({X: X_train, Y: Y_train}))
        print("Test Accuracy:", accuracy.eval({X: X_test, Y: Y_test}))

        return parameters

我們來正式執行一下模型，請注意，這次的執行時間大約在5-8分鐘左右，如果在epoch = 100的時候，你的epoch_cost = 1.01645776539的值和我相差過大，那麼你就立即停止，回頭檢查一下哪裡出了問題。

parameters = model(X_train, Y_train, X_test, Y_test)

#結果
epoch = 0    epoch_cost = 1.85570189447
epoch = 100    epoch_cost = 1.01645776539
epoch = 200    epoch_cost = 0.733102379423
epoch = 300    epoch_cost = 0.572938936226
epoch = 400    epoch_cost = 0.468773578604
epoch = 500    epoch_cost = 0.3810211113
epoch = 600    epoch_cost = 0.313826778621
epoch = 700    epoch_cost = 0.254280460603
epoch = 800    epoch_cost = 0.203799342567
epoch = 900    epoch_cost = 0.166511993291
epoch = 1000    epoch_cost = 0.140936921718
epoch = 1100    epoch_cost = 0.107750129745
epoch = 1200    epoch_cost = 0.0862994250475
epoch = 1300    epoch_cost = 0.0609485416137
epoch = 1400    epoch_cost = 0.0509344103436
Parameters have been trained!
Train Accuracy: 0.999074
Test Accuracy:0.725

思考：

• 你的模型似乎足夠大，能很好地適應訓練集。然而，考慮到train精度和test精度之間的差異，您可以嘗試新增L2或dropout正則化以減少過擬合。
• 將session看作是訓練模型的程式碼塊。每次在minibatch上執行session時，它都會訓練引數。總而言之，您已經重複執行session很多次了(1500次epoch)，直到您獲得了經過良好訓練的引數。

2.7 - 測試你自己的圖片（選做）

import scipy
from PIL import Image
from scipy import ndimage

## START CODE HERE ## (PUT YOUR IMAGE NAME) 
my_image = "thumbs_up.jpg"
## END CODE HERE ##

# We preprocess your image to fit your algorithm.
fname = "images/" + my_image
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(64,64)).reshape((1, 64*64*3)).T
my_image_prediction = predict(my_image, parameters)

plt.imshow(image)
print("Your algorithm predicts: y = " + str(np.squeeze(my_image_prediction)))

#結果：
Your algorithm predicts: y = 3

你確實應該“豎起大拇指”的圖（代表1），儘管正如你所看到的，演算法似乎對它的分類不正確。原因是訓練集不包含任何“豎起大拇指”的圖片，所以模型不知道如何處理它!我們稱之為"不匹配的資料分佈"這是下一門關於"構建機器學習專案"的課程之一。

總結：

• TF中的兩個主要物件類是張量（Tensors）和運算（Operators）
• 當您在tensorflow中編碼時，您必須採取以下步驟:

•  就像在model()中看到的那樣，可以多次執行這個靜態圖
• 在“optimizer”物件上執行session時，將自動執行反向傳播（backpropagation）和優化（optimization）。