2. 程式人生 > >吳恩達Coursera深度學習課程 DeepLearning.ai 提煉筆記（1-3）-- 淺層神經網路

吳恩達Coursera深度學習課程 DeepLearning.ai 提煉筆記（1-3）-- 淺層神經網路

阿新 • • 發佈：2019-01-07

以下為在Coursera上吳恩達老師的DeepLearning.ai課程專案中，第一部分《神經網路和深度學習》第三週課程“淺層神經網路”部分關鍵點的筆記。筆記並不包含全部小視訊課程的記錄，如需學習筆記中捨棄的內容請至Coursera 或者 網易雲課堂。同時在閱讀以下筆記之前，強烈建議先學習吳恩達老師的視訊課程。

同時我在知乎上開設了關於機器學習深度學習的專欄收錄下面的筆記，方便在移動端的學習。歡迎關注我的知乎：大樹先生。一起學習一起進步呀！^_^

神經網路和深度學習—淺層神經網路

1. 神經網路表示

簡單神經網路示意圖：

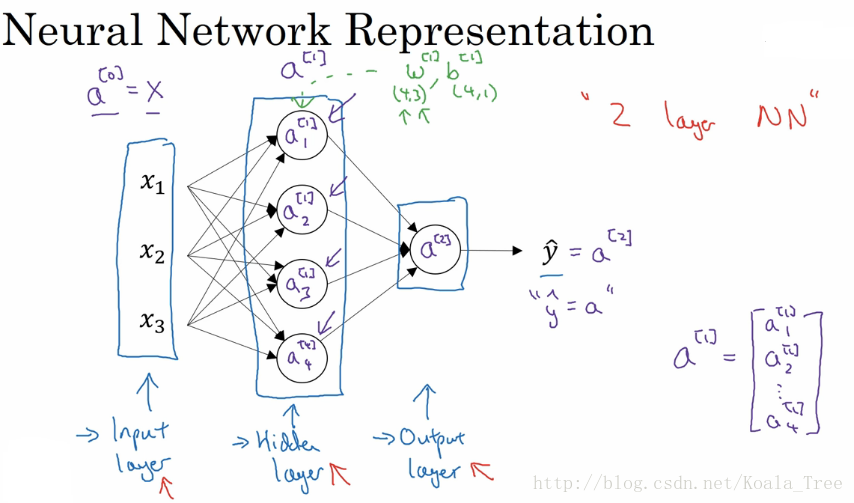
還在路上，稍等...

神經網路基本的結構和符號可以從上面的圖中看出，這裡不再複述。

主要需要注意的一點，是層與層之間引數矩陣的規格大小：

  • 輸入層和隱藏層之間
    • w[1]−>(4,3)：前面的4是隱層神經元的個數，後面的3是輸入層神經元的個數；
    • b[1]−>(4,1)：和隱藏層的神經元個數相同；
  • 隱藏層和輸出層之間
    • w[1]−>(1,4)：前面的1是輸出層神經元的個數，後面的4是隱層神經元的個數；
    • b[1]−>(1,1)：和輸出層的神經元個數相同；

由上面我們可以總結出，在神經網路中，我們以相鄰兩層為觀測物件，前面一層作為輸入，後面一層作為輸出，兩層之間的w引數矩陣大小為(nout,nin)，b引數矩陣大小為(nout,1)，這裡是作為z=

wX+b的線性關係來說明的，在神經網路中，w[i]=wT。

在logistic regression中，一般我們都會用(nin,nout)來表示引數大小，計算使用的公式為：z=wTX+b，要注意這兩者的區別。

2. 計算神經網路的輸出

除輸入層之外每層的計算輸出可由下圖總結出：

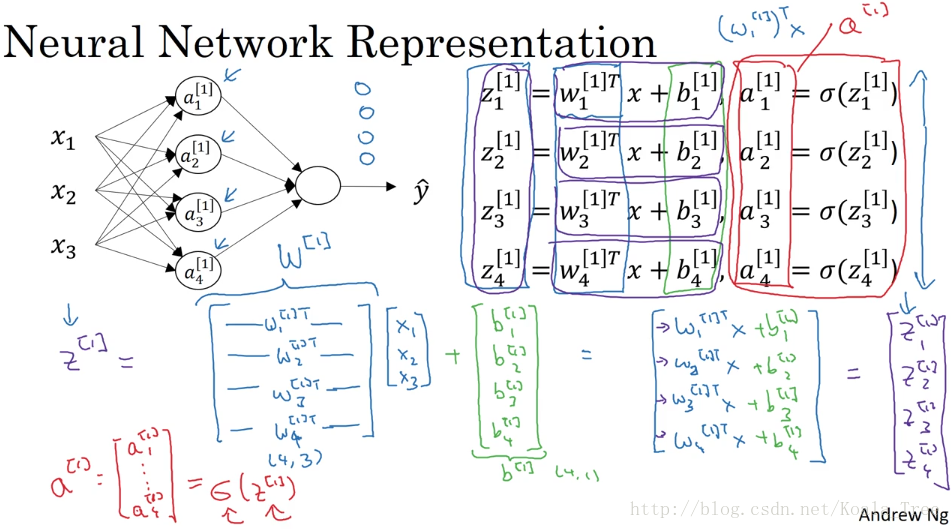
還在路上，稍等...

其中，每個結點都對應這兩個部分的運算，z運算和a運算。

在程式設計中，我們使用向量化去計算神經網路的輸出：

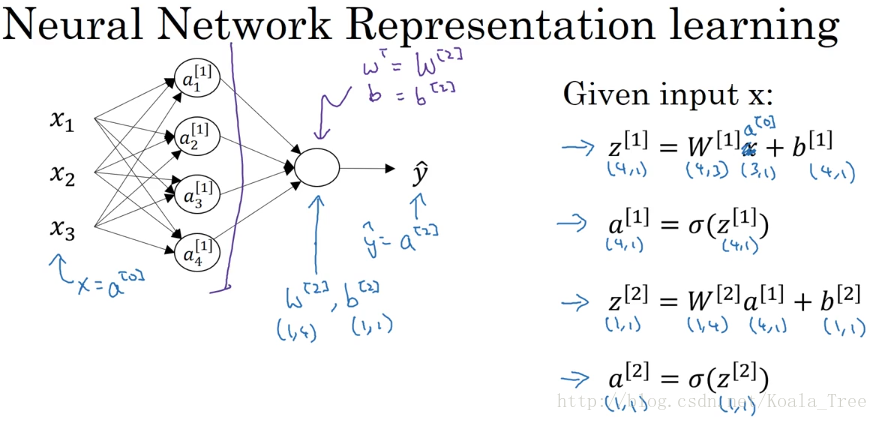
還在路上，稍等...

在對應圖中的神經網路結構，我們只用Python程式碼去實現右邊的四個公式即可實現神經網路的輸出計算。

3. 向量化實現

假定在m個訓練樣本的神經網路中，計算神經網路的輸出，用向量化的方法去實現可以避免在程式中使用for迴圈，提高計算的速度。

下面是實現向量化的解釋：

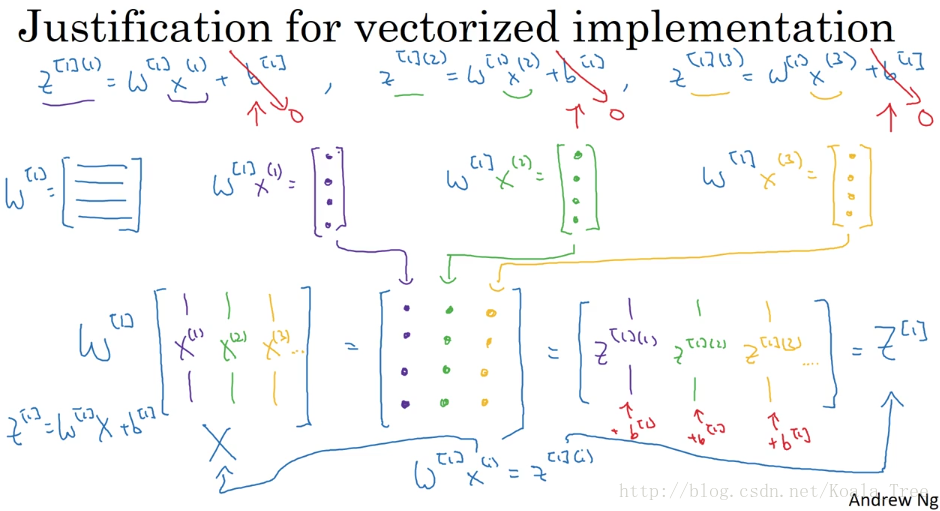
還在路上，稍等...

由圖可以看出，在m個訓練樣本中，每次計算都是在重複相同的過程，均得到同樣大小和結構的輸出，所以利用向量化的思想將單個樣本合併到一個矩陣中，其大小為(xn,m)，其中xn表示每個樣本輸入網路的神經元個數，也可以認為是單個樣本的特徵數，m表示訓練樣本的個數。

通過向量化，可以更加便捷快速地實現神經網路的計算。

4. 啟用函式的選擇

幾種不同的啟用函式g(x)：

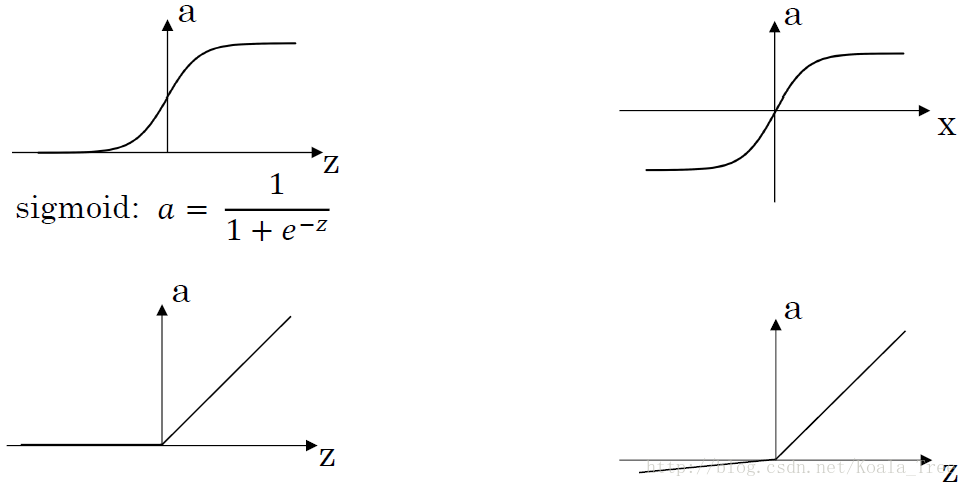
還在路上，稍等...
  • sigmoid：a=11+e−z
    • 導數：a′=a(1−a)
  • tanh：a=ez−e−zez+e−z
    • 導數：a′=1−a2
  • ReLU（修正線性單元）：a=max(0,z)
  • Leaky ReLU：a=max(0.01z,z)

啟用函式的選擇：

sigmoid函式和tanh函式比較：

  • 隱藏層：tanh函式的表現要好於sigmoid函式，因為tanh取值範圍為[−1,+1]，輸出分佈在0值的附近，均值為0，從隱藏層到輸出層資料起到了歸一化（均值為0）的效果。
  • 輸出層：對於二分類任務的輸出取值為{0,1}，故一般會選擇sigmoid函式。

然而sigmoid和tanh函式在當|z|很大的時候，梯度會很小，在依據梯度的演算法中，更新在後期會變得很慢。在實際應用中，要使|z|儘可能的落在0值附近。

ReLU彌補了前兩者的缺陷，當z>0時，梯度始終為1，從而提高神經網路基於梯度演算法的運算速度。然而當z<0時，梯度一直為0，但是實際的運用中，該缺陷的影響不是很大。

Leaky ReLU保證在z<0的時候，梯度仍然不為0。

在選擇啟用函式的時候，如果在不知道該選什麼的時候就選擇ReLU，當然也沒有固定答案，要依據實際問題在交叉驗證集合中進行驗證分析。

5. 神經網路的梯度下降法

以本節中的淺層神經網路為例，我們給出神經網路的梯度下降法的公式。