題目連結：https://www.nowcoder.com/acm/contest/188/C 題目大意：給你n個點，他們用n-1條邊無向聯通，,每條邊都有一個長度，給你一個初始的起點，讓你起點出發，求經過每個點一次的最短路。

輸入： 第一行兩個整數 n,x,代表點數,和起點的位置 第二到第n行,每行三個整數 u,v,w,表示u和v之間有一條長為w的道路 輸出： 一個數表示答案 思路：首先看到這道題，就想起前幾天才學習的最短路，發現這個圖是棵樹，

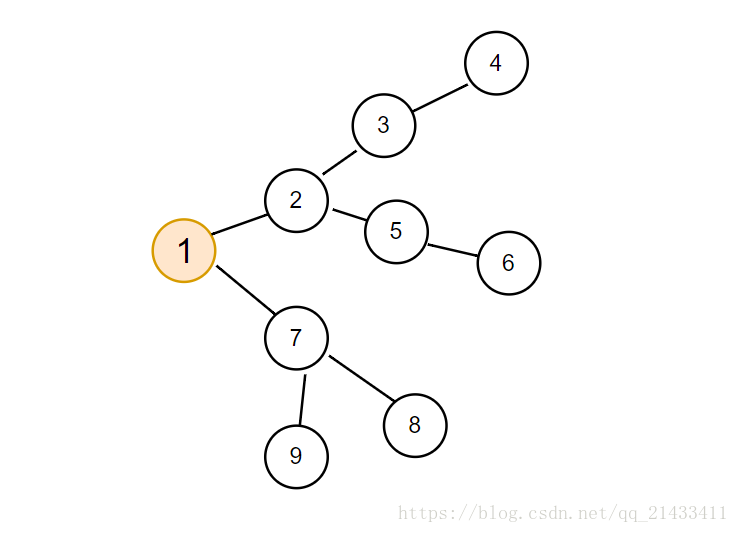
然而發現這道題的規律是：以起點為根節點，除了一條從根節點到葉節點的路徑只走一遍，其餘的路徑都要走兩遍。

那麼 S(最短路)=2*S(所有邊)-S(從根節點到葉節點的最長路) 所以現在只要找到這條從根節點到葉節點的最長路就行了。

求從根節點到葉節點的最長路：只要從根節點開始對每一條與根節點相連的邊都跑一遍，直到這個節點沒有路，那麼這就是一條從根節點到葉節點的路徑，記錄最大的路徑。

這裡用bfs搜尋一遍就好了， 對1-2這條路，把與2相連的2-3， 2-5加入佇列，標記2節點表示已經走過，並記錄這條路的長度，再從佇列top一條路並且pop，重複上述過程。只到這個節點沒有路，那麼這就是一條從根節點到葉節點的路徑，記錄最大的路徑。等到佇列為空，就把1-7加入佇列，重複上述過程，一直把與1節點的路都跑一遍就找到從根節點到葉節點的最長路了。

思考：因為是第一次做最短路的題，所以用vector存鄰接表，當時寫完程式碼，一直WA，後來找到原因是存圖只存了單向邊，改完AC。

#include<bits/stdc++.h>
using namespace std;

struct dt{
    long long to;//邊的終點
    long long v; //邊的長度
    long long s; //從起點到邊的終點的總路程

}now;

vector<dt> g[50005];
stack<dt> sk;//佇列

int vis[50005];
long long s1=0;//從根節點到葉節點的最長路
void bfs()     //找從根節點任意一條邊開始的所有路
{
    while(!sk.empty())
    {
        now=sk.top();//得到佇列的邊
        sk.pop();
        long long m=now.to;
        long long v=now.v; 

        vis[m]=1;//標記節點
        int p=0; //記錄這個節點是否還有路
        for(vector<dt>:: iterator k = g[m].begin();k != g[m].end(); ++k)
        {
            dt now1=*k;
            if(vis[now1.to]==0)//節點沒有標記
            {
                vis[now1.to]=1;
                p=1;
                dt now1=*k;
                now1.s += now.s;
                sk.push(now1);
            }
        }
        if(p==0)//如果這個節點沒有路了,now.s就為一條從根節點到葉節點的路徑
            s1=max(s1, now.s);
    }

}

int main()
{
    int n, m;
    long long s=0;
    scanf("%d%d",&n,&m);
    long long x, y, v;
    for(int i=0;i<n-1;i++)
    {
        scanf("%lld%lld%lld",&x,&y,&v);
        now.to=y;
        now.v=v;
        now.s=v;
        g[x].push_back(now);//存x->y的邊
        now.to=x;
        now.v=v;
        now.s=v;
        g[y].push_back(now);//存y->x的邊
        s+=v;
    }

    for(vector<dt>:: iterator k = g[m].begin();k != g[m].end(); ++k)
    {
        memset(vis, 0,sizeof(vis));
        vis[m]=1;
        sk.push(*k);//與根節點相連的邊加入佇列
        bfs();      //找從根節點任意一條邊開始的所有路
    }
    printf("%lld\n",s*2-s1);

    return 0;
}