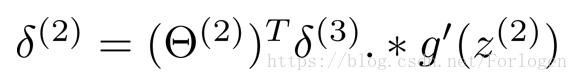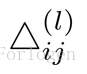一、代價函式

前面學習了有關神經網路的基本知識和一些小的例子，這節課學習更深層次的東西，首先來看代價函式。

我們假設我們的神經網路如圖所示，給定資料集D={(x1,y1)…(xn,yn)}，x表示輸入訊號，y表示輸出訊號，L表示神經網路的層數 Sl表示每一層上神經元單元的個數。

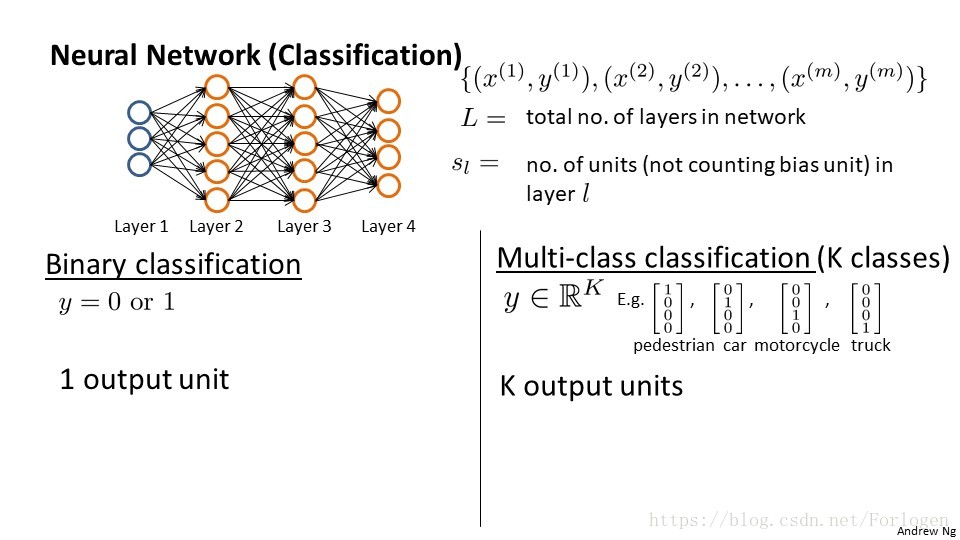
在分類問題中，我們可以粗略的分為兩類 1. 二分類問題 在輸出單元我們可以用1表示正例，0表示負例，或者相反； 2. 多分類問題 在多分類問題中，我們不用單個的不同數字表示不同的類別，而是採用不同向量的方式，K的類別我們就是用K個向量區分

在前面的Logistic迴歸中，我們的代價函式J(θ)如圖所示，我們需要輸出變數可以分開類別，所以輸出變數只有一個y，而在神經網路中 我們的輸出問題可能會有K個類別，因此我們的輸出單元需要K維的向量，那麼我們的代價函式就如上圖所示。

複雜的結構背後的思想和前面的仍然一樣，我們希望通過計算代價來看一下預測的值和真實的值的誤差，選擇誤差最小的那一個。 但在多分類問題中，我們通常會給出K個預測的輸出，我們利用迴圈對每一個特徵都預測k個不同的結果，然後在迴圈中選擇K個預測中 可能性最高的那一個，再與真實的值進行比較。

二、後向傳播演算法

這節主要學習神經網路中最重要的一個演算法：後向傳播演算法。 在前面我們學習了前向傳播演算法，這裡假設我們的代價函式如上圖所示，目標是找到使代價函式值最小的引數，為此我們需要計算J(θ)的偏導數。

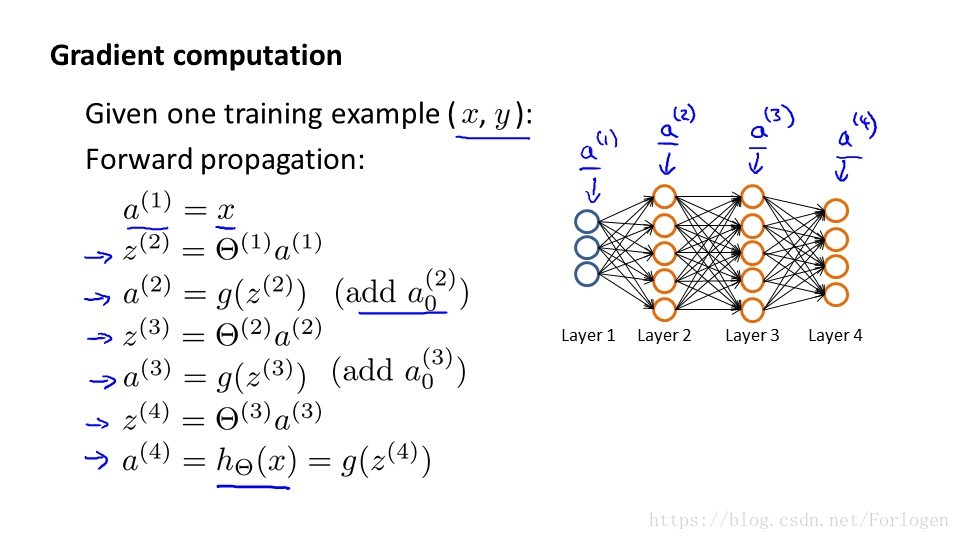
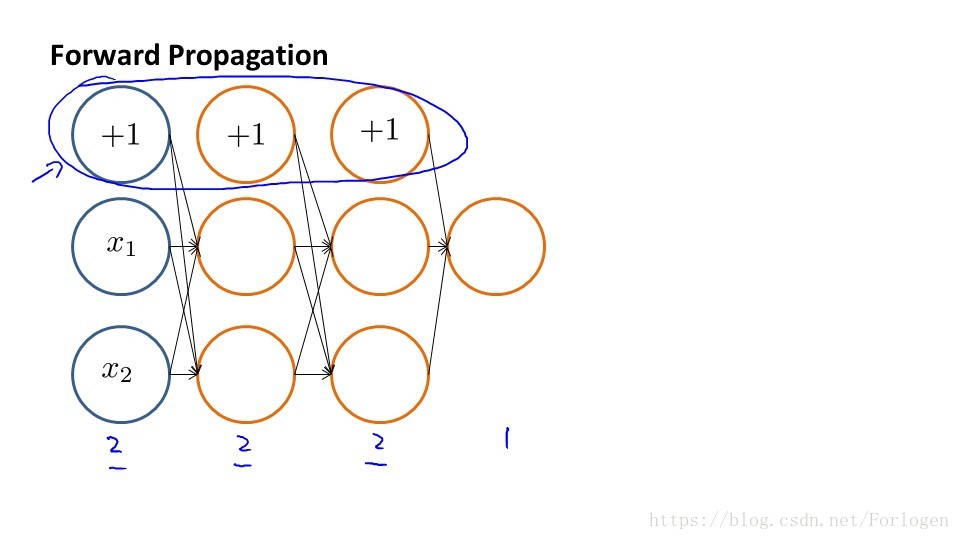
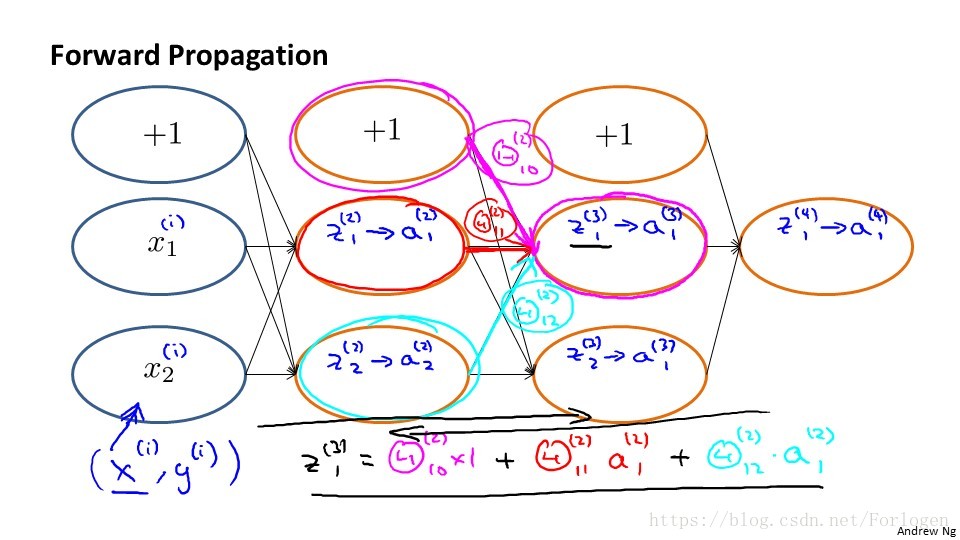
前向傳播演算法如上圖所示，假設訓練集只有一個例項（x1,y1），我們的神經網路有四層，輸出層有四個神經單元，具體的計算過程如圖所示。

而在後向傳播演算法中，我們需要從最後一層開始計算，誤差用δ表示，每一層的計算過程如上。 首先我們計算輸出層，也就是這裡的第四層，它的過程為： 然後我們利用這個值帶入公式計算第三層的誤差： 這裡的後的g(z)是一個S形函式的導數，他就等於a(3).(1-a(3))，而*前面的部分是權重導致的誤差和，同理我們計算第二層的誤差：

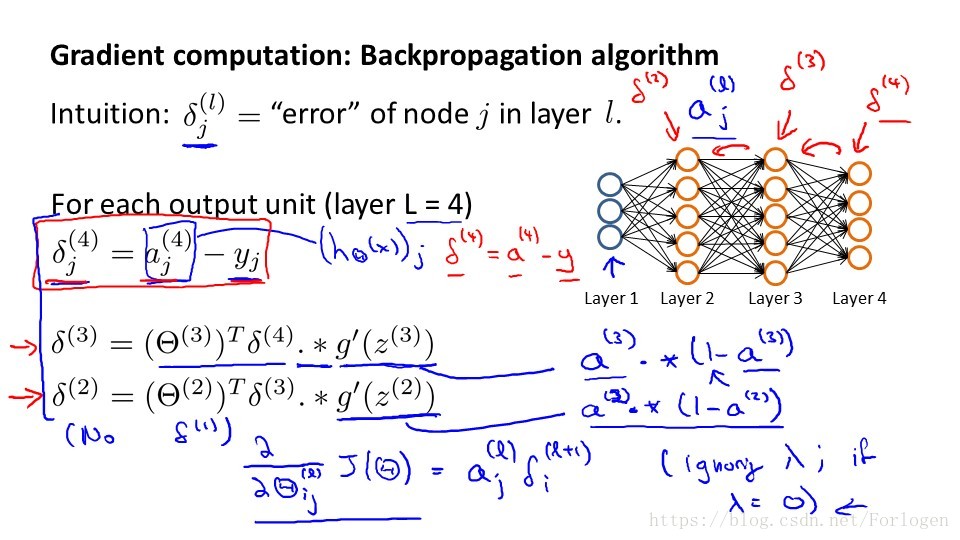
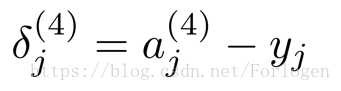
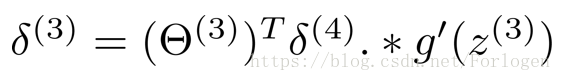
因為第一層就是我們的輸入層，沒有誤差這一說，所以不必計算。當我們將所有的誤差都計算出來後，便可以計算代價函式的偏導數， 假設我們不做歸一化處理，計算公式如下：

表示式中，l 表示是第幾層；j表示計算層神經單元的下標，也就是下一層第j個輸入變數的下標；I 表示下一層誤差單元的下標， 也就是受到權重矩陣中第 i行影響的下一層中誤差單元的下標。

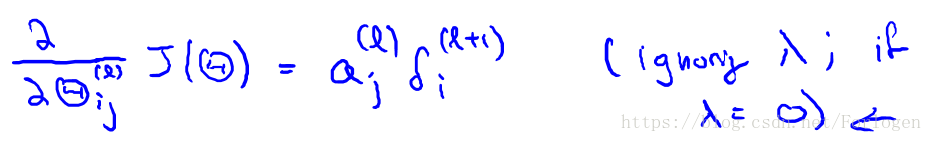
一般情況下，我們需要計算每一層的誤差單元，同樣我們需要為整個訓練集計算誤差單元，此時誤差單元也是矩陣，用

表示第l層的第i的神經單元受到第j個引數而導致的誤差，演算法虛擬碼如下：

在求出誤差單元的值後，我們計算代價函式的偏導數，如圖左下角所示的公式。

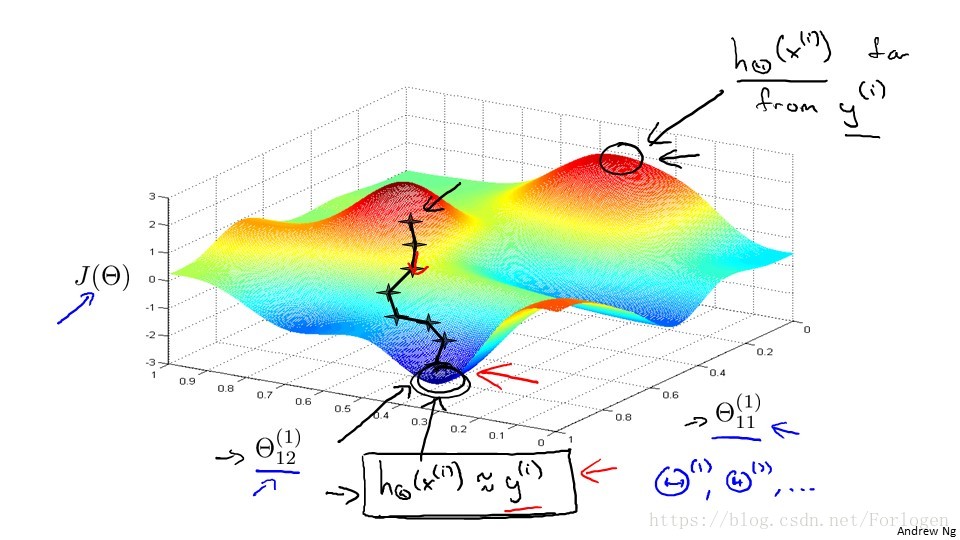
三、Backpropagation intuition

前向傳播演算法如下，這裡我們設定每一層的偏置單元都為+1：

計算過程示意圖如下： 反向傳播演算法如下：

下面介紹了怎樣把引數從矩陣展開成享兩年，便於在高階最優化步驟中使用：

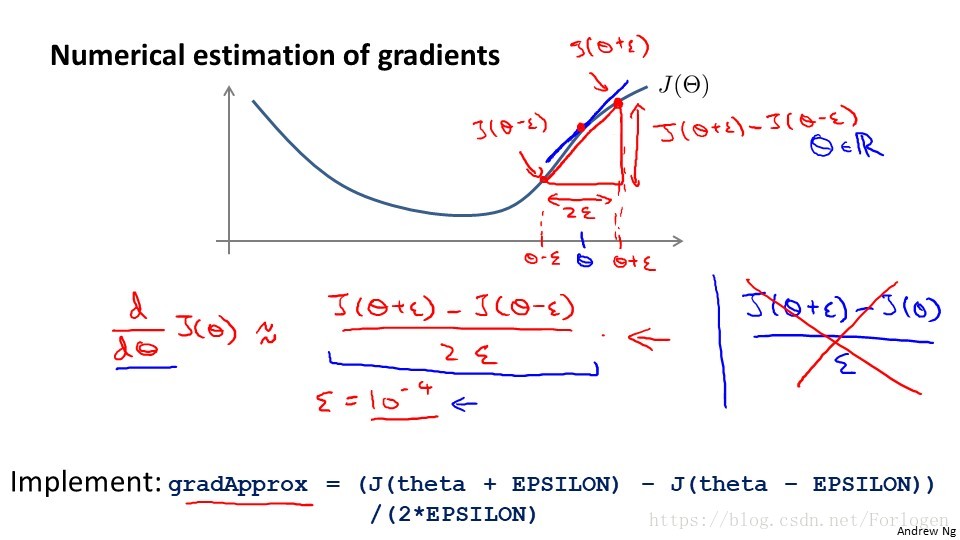
在神經網路等模型中使用梯度下降演算法計算時，如果在計算過程中出現了一些小的錯誤，雖然整體下降的趨勢不會改變，但是最後的結果卻不是最優解了。 為了解決這個問題，我們使用一種叫梯度檢驗的方法，它通過估計梯度值來檢驗我們計算的導數值 是不是我們需要的來實現。

四、梯度檢測

那麼如何實現呢？在微積分中我們學過以直代曲，這裡我們這裡沿著切線方向選擇兩個非常近的點然後計算量的點的平均值來估計梯度。 例如我們在x=θ的左右兩側取一個距離很小的值（常取0.001），然後計算兩個代價的平均，用來估計在θ處的代價值。

當θ是一個向量時，我們需要檢驗偏導數，道理是一樣的，學過微積分的應該很容易理解。

五、引數的初始化

隨機初始化，任何優化演算法的引數都需要一定的初始值，如果我們都設定為0或是相同的非零數，那麼下一層神經單元的計算值都將一樣，顯然是不可行的。 我們通常初始化為一個很小的範圍之間的隨機值。

六、總結

網路結構：第一件要做的事是選擇，即決定多 少層以及每分別有網路結構：即決定多 少層以及每分別有少個單元。第一層的單元數即我們訓練集特徵量。 最後一層的單元數是我們訓練集結果類量。 如果隱藏層數大於 如果隱藏層數大於 確保每個隱藏層的單元數 相同，通常情況下，確保每個隱藏層的單元數 相同通常情況下，確保每個隱藏層的單元數 相同通常情況下越多好。

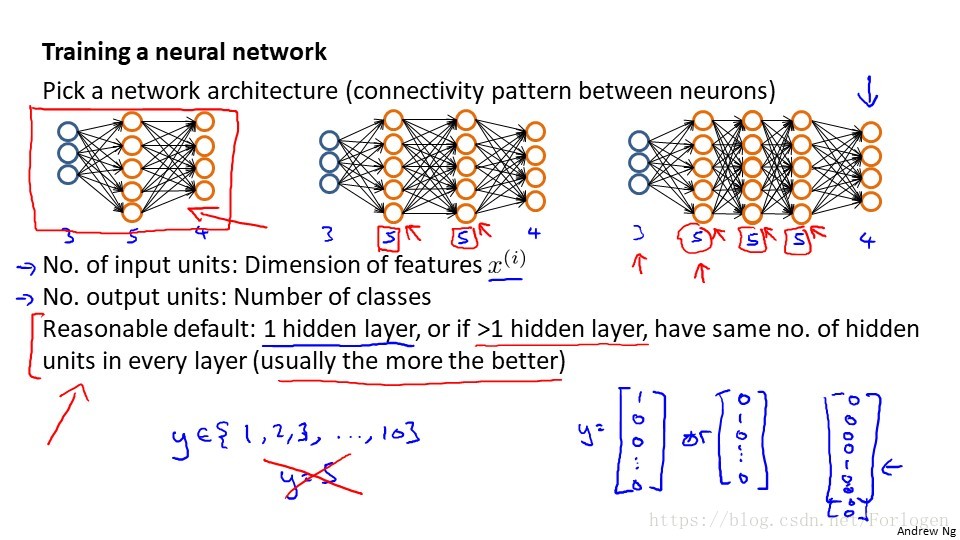
我們需要決定隱藏層的單元個數和每個中間層的單元數。

訓練神經網路的步驟如下： 1. 引數的隨機初始化 2. 利用正想傳播演算法計算所有的hθ(x) 3. 編寫計算代價函式的程式碼 4. 利用反向傳播演算法計算所有的偏導數 5. 利用數值檢驗方法檢驗這些偏導數 6. 使用優化演算法來最小化代價函式