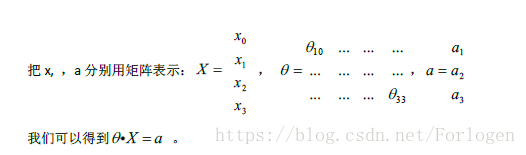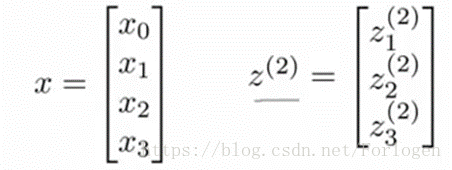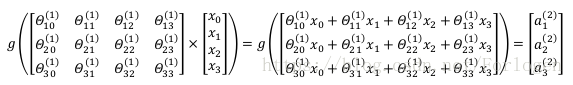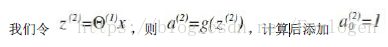一、Non-linearhypotheses

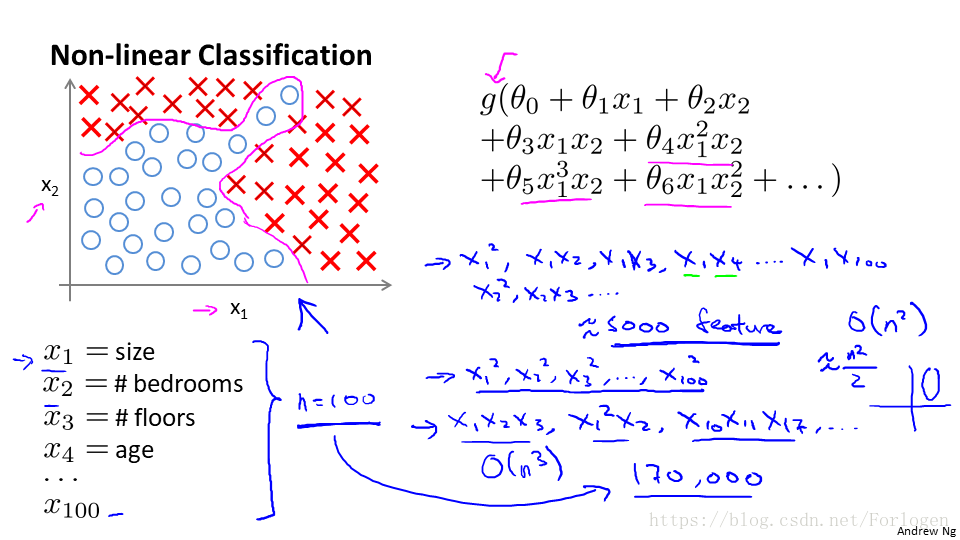
在一般分類問題中，我們可以使用一條直線或是曲線，將其進行一個正確的分類；在如下類似的多分類問題中，我們找到一條曲線進行合理的劃分。

在特徵較少時我們使用Logistic迴歸取得很好的效果，此時表示式中只有x1和x2兩個變數的組合。但如果我們的特徵很多時，比如有100個特徵，比如在房價預測問題中，特徵的數目就會有很多，我們如果仍然使用前面的方法去做的話，特徵的組合的陣列會達到一個驚人的數目，對於當前使用的演算法來說，需要計算的時間太長，長到使用者無法接受。

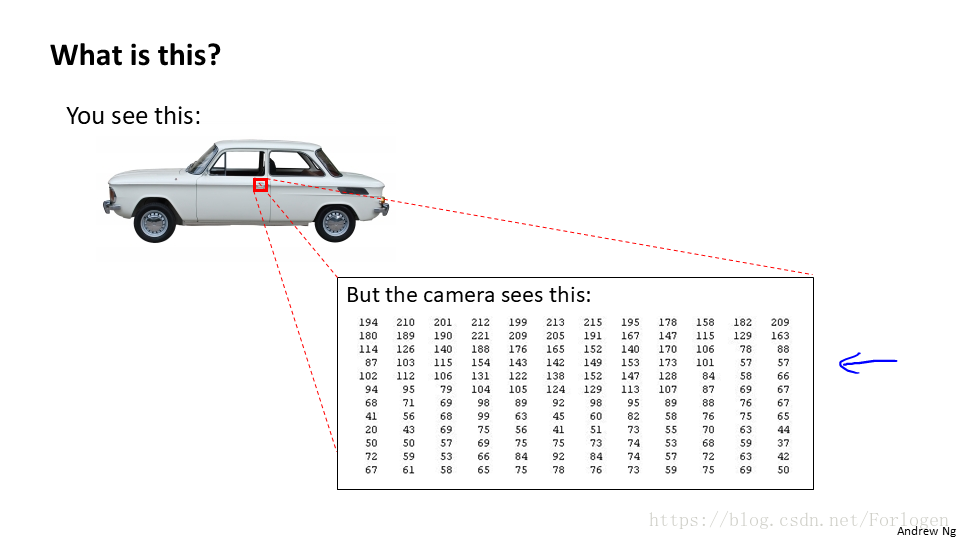
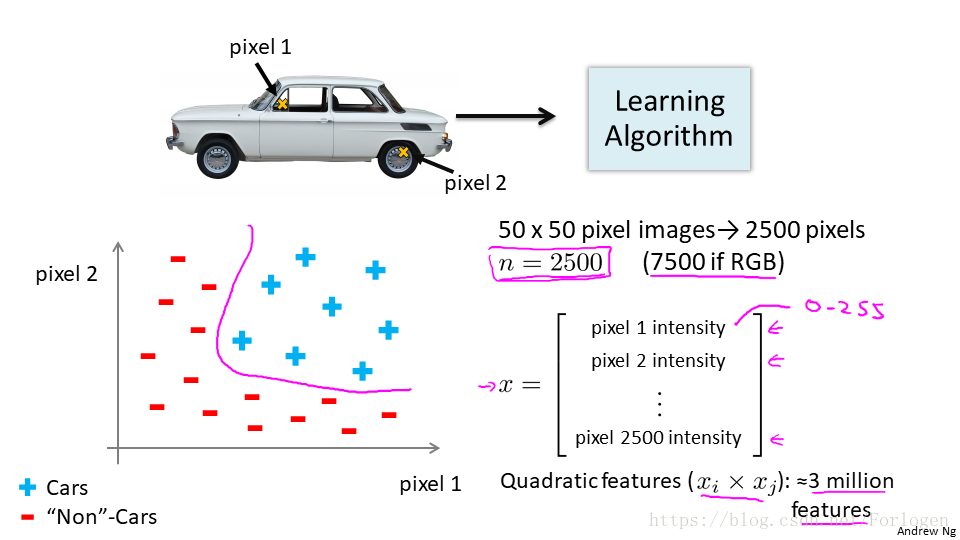
在實際的應用問題中，比如我們需要來識別上圖是不是一輛汽車，對於人來說，我們可以一眼就給出答案，但是在計算機看來是一個一個的灰度值，假設畫素是50*50，那麼特徵就會達到2500個，使用前面的演算法就行特徵的組合，特徵組合結果將會有3百萬個之多，如果是RGB，那麼結果將會更多，顯然不適用前面的迴歸模型。

二、Neurons and the brain

如果想直到更多關於神經網路的歷史發展，可以通過相關的書籍資料得到。

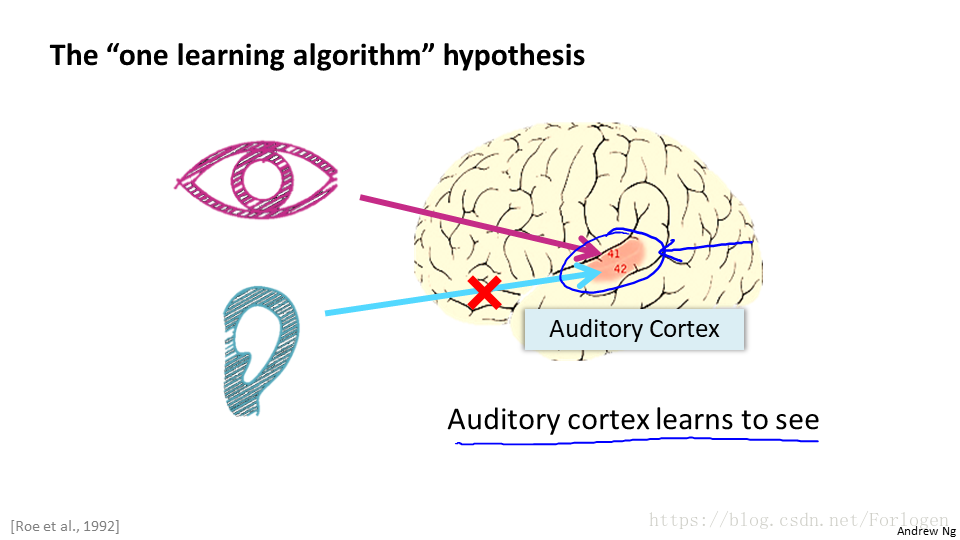
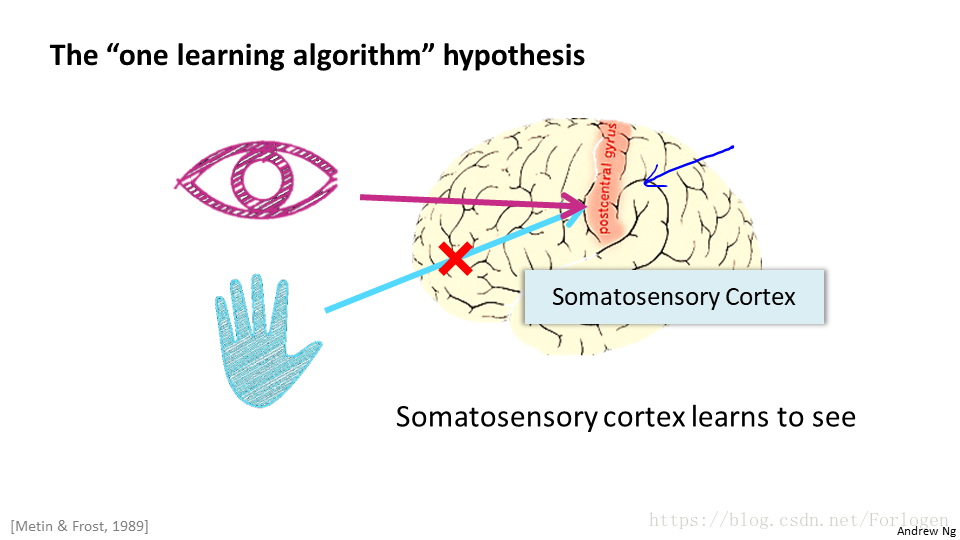
之前，科學家通過一系列的“神經重連實驗”，瞭解到通過將處理某個功能的大腦皮層與其他功能的神經相連，通過一定量的學習，它就會有新的功能。那我們能不能寫一個東西來模擬實現大腦的這種學習功能呢，這時神經網路模型便應時而出。

三、Model Representation

那麼我們具體怎麼實現這個模型呢？在此之前我們就需要了解大腦是如何實現這一系列的工作的。

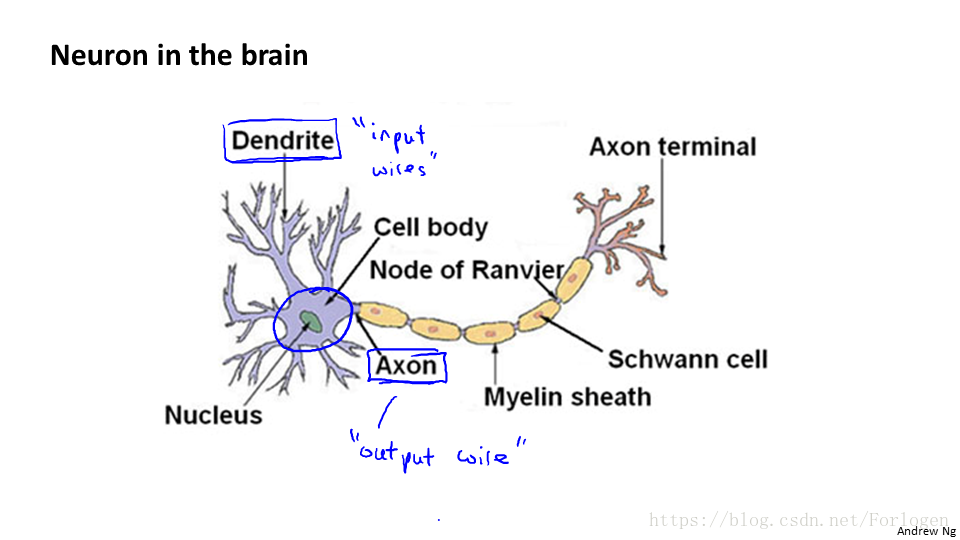
大腦中神經元如圖所示，它包括神經核、許多的樹突和一個軸突，這裡我們將其分別成為處理單元、許多輸入和一個輸出。神經網路就是由大量的神經元所組成的一個網路，他們通過電脈衝相互交流，這裡是一條連線到輸入神經，或者連線到另一個神經元樹突的神經，接下來這個神經元接收到這條訊息，做計算，然後將結果傳給其他的神經元，這就是工作的一般方式。

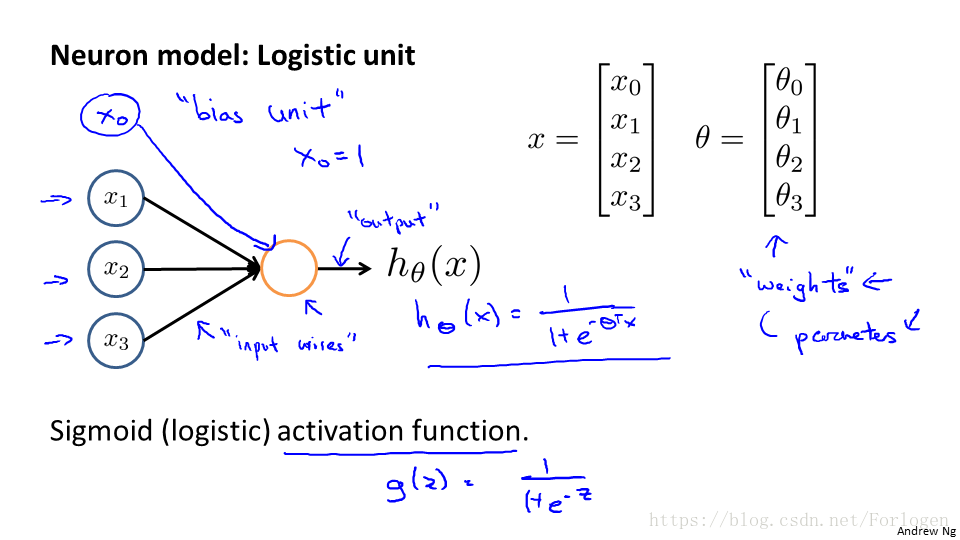
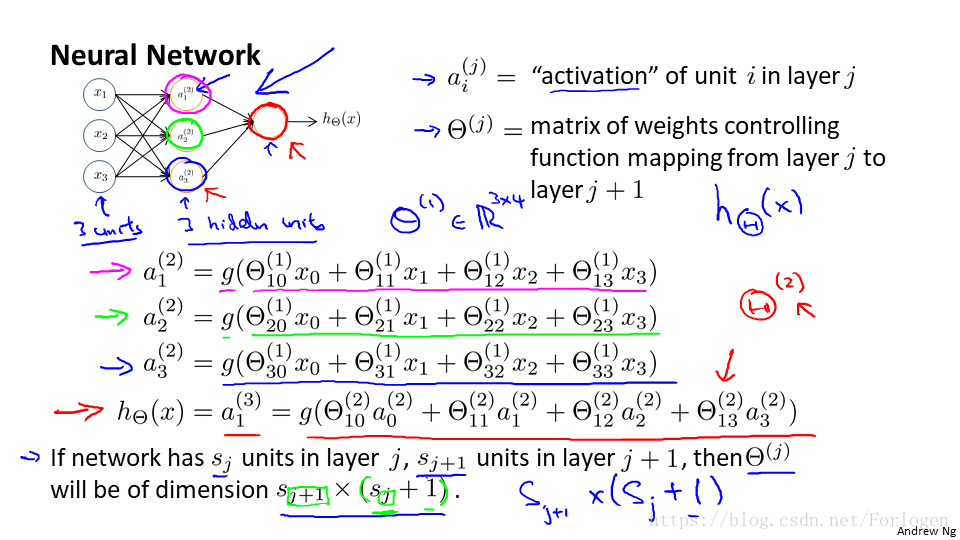
神經網路就是建立在很多的神經元上的，每一個神經元（啟用單元）就是一個學習模型，它接受一些特徵的輸入，根據自身模型的一個計算給出相應的輸出值。如上圖所示，輸入的x1、x2、x3經過h（x）的計算從而得到一個輸出值，通常為了便於向量化，我們會增加一個x0，對應的引數（這裡稱為權重）也要改變。

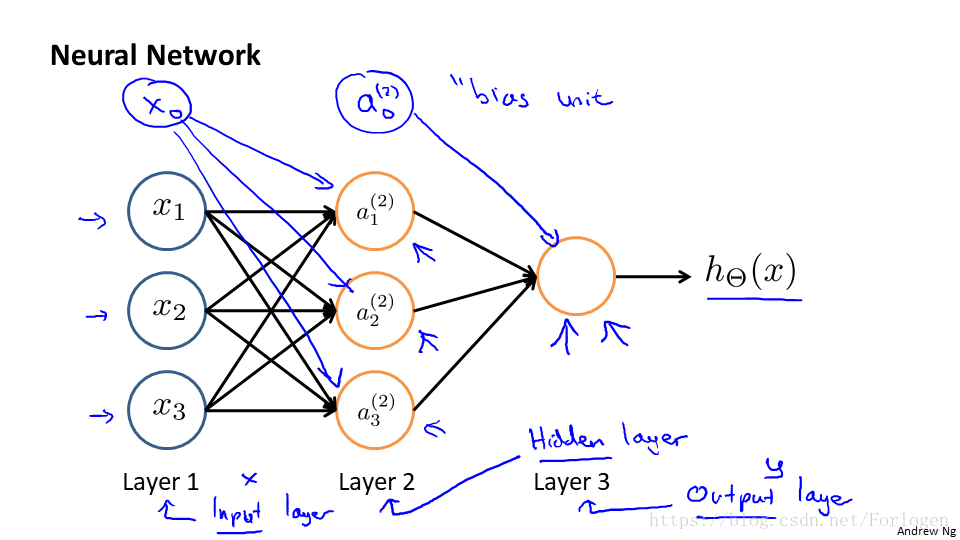
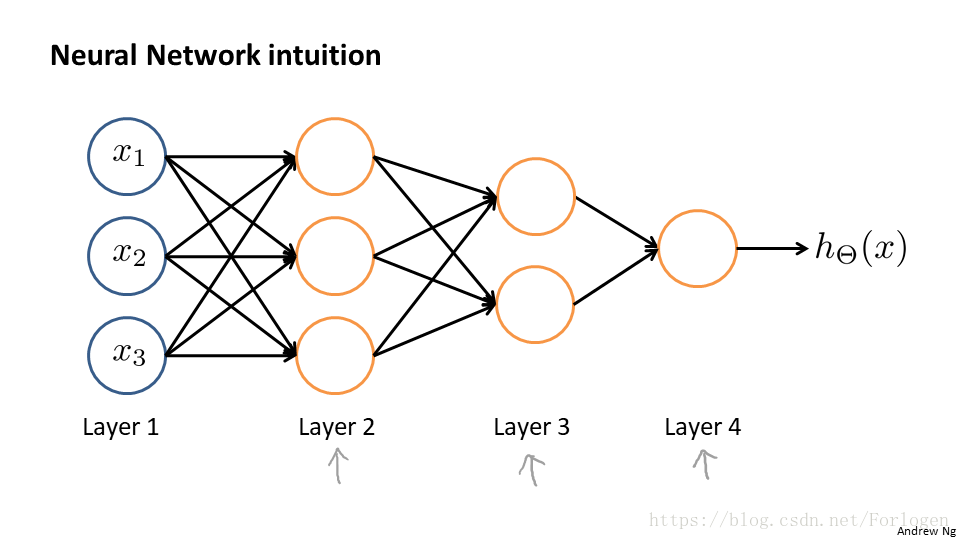
由此我們就可以得到一個如下所示的簡單的三層神經網路的模型：

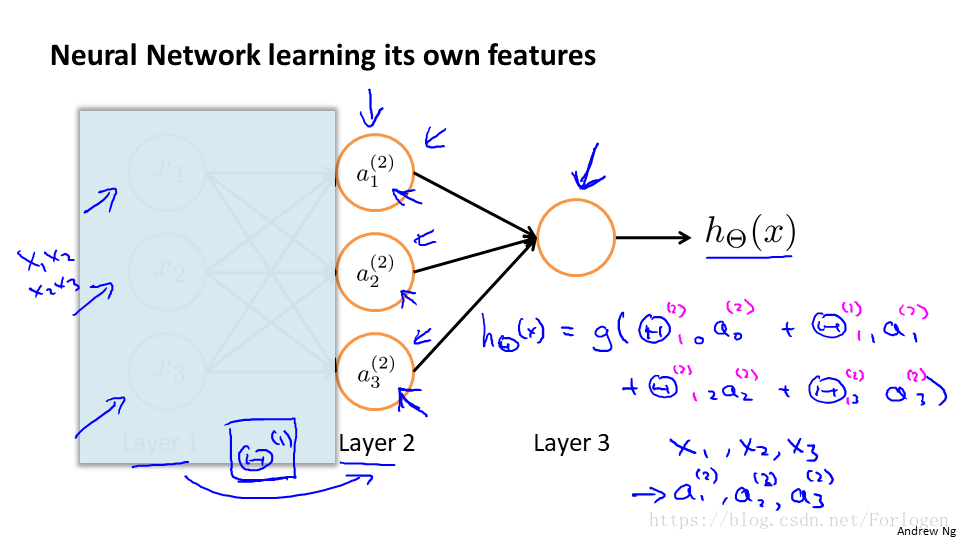
圖中的x1、x2、x3是輸入單元，我們可以將原始的資料給它，a1、a2、a3是中間單元，處理輸入的資料將結果傳給下一層。如圖所示的模型中，包括三層：輸入層（input layer）、隱藏層（hidden layer）和輸出層（output layer），此外為了向量化我們加入了偏置單位（bias unit）。其中的字母標記解釋如下：

那麼上圖中啟用單元相應的表達就可以是這樣：

向量化的效果：

通過模型的訓練我們就可以得到一個結果。上面的模型中的每一個a都是有前面傳入的所有x和相應的權重值決定的，所以我們成這樣的從左到右的演算法為前向傳播演算法。

我們來計算一下上面模型第二層的值：
我們首先向量化，結果為：

然後我們進行向量的相乘：

為了簡化計算，我們做出如下的操作：

那麼我們的計算就變成了：

我們將左半部分不看，那麼看到的右半部分將其看成是按Logistic 迴歸進行的，我們同樣給定權重，h(x)就變成了如圖所示的形式。

在普通的迴歸演算法中，我們得到一系列的原始特徵，儘管可以進行不同的線性組合，但還是離不開給定的特徵，而神經網路只有在第一層給定原始特徵，從第三層起，我們輸入的實際是神經網路模型自己學習的更高階的特徵，這樣我們就不再受原始特徵的束縛。

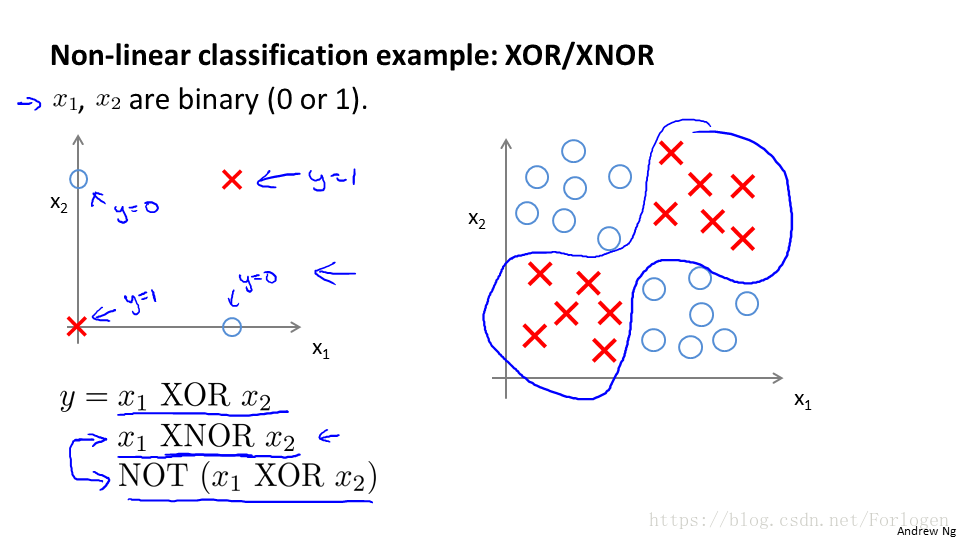
在上圖所示的非線性分類的例子中，我們的x1和x2只取0和1兩個值，當給定的資料較多時，我們找到一個合適的決策邊界，用表示式寫就是圖中y的結果。那麼我們怎麼使用使用神經網路實現這個看起來複雜的結果呢？需要從簡單的看起。

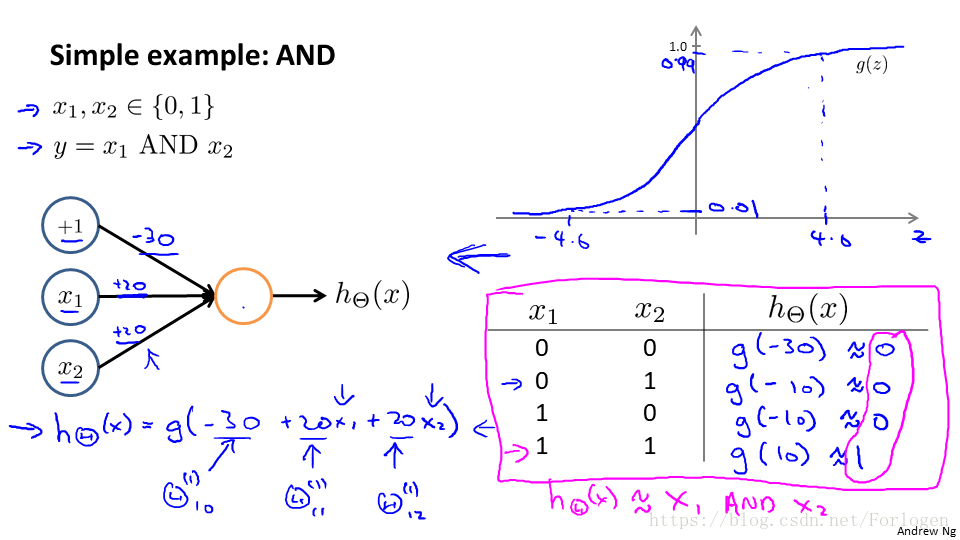
上圖表示了AND與運算的實現，利用前面學過的知識，我們知道g(x)的函式圖形如圖所示，在輸入的x0,x1,x2中，我們給定權重為-30、+20、+20，帶入到給g（x）的表示式，結果如圖中表格所示，我們可以正確實現AND運算。

同理OR運算如下圖所示：

NOT運算如圖所示：

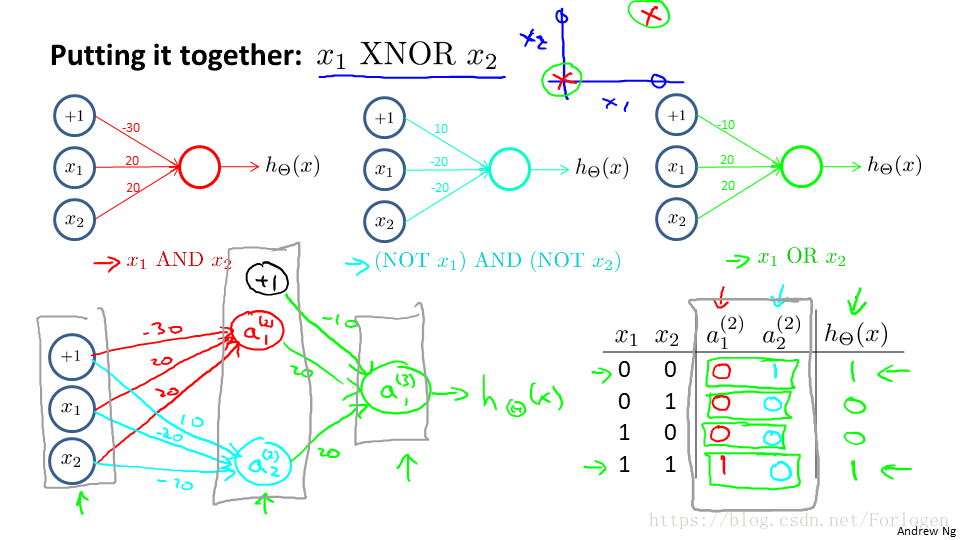
那麼將上面的三個進行結合就可以實現想要實現的複雜運算。

那麼計算的結果如表中所示，我們可以看到可以正確實現。

知道了簡單的實現後，我們就可以將不同的簡單的神經網路組成更加複雜的神經網路模型。

四、Multi-class classifition

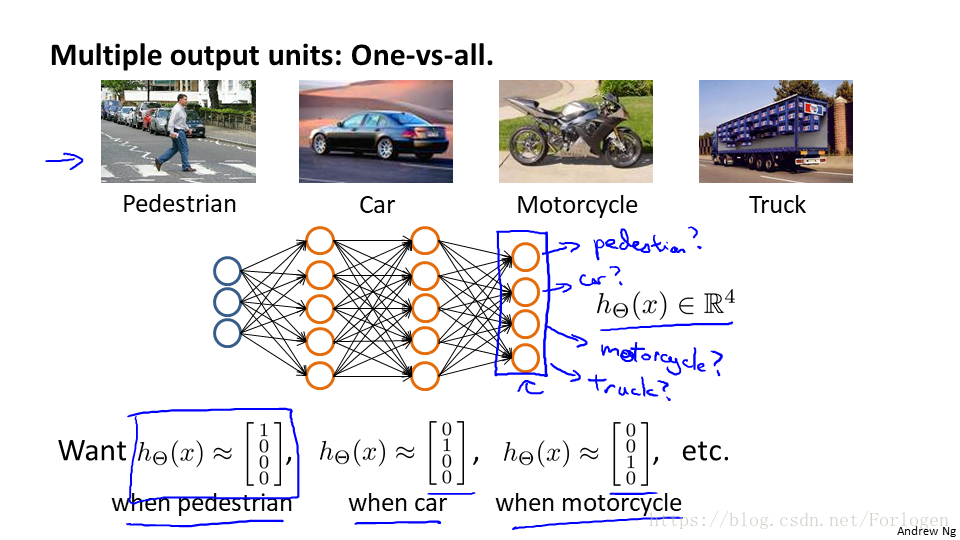
對於簡單的二分類問題，我們可以根據輸出是0還是1來進行判別，但如果是下圖的多分類問題時：

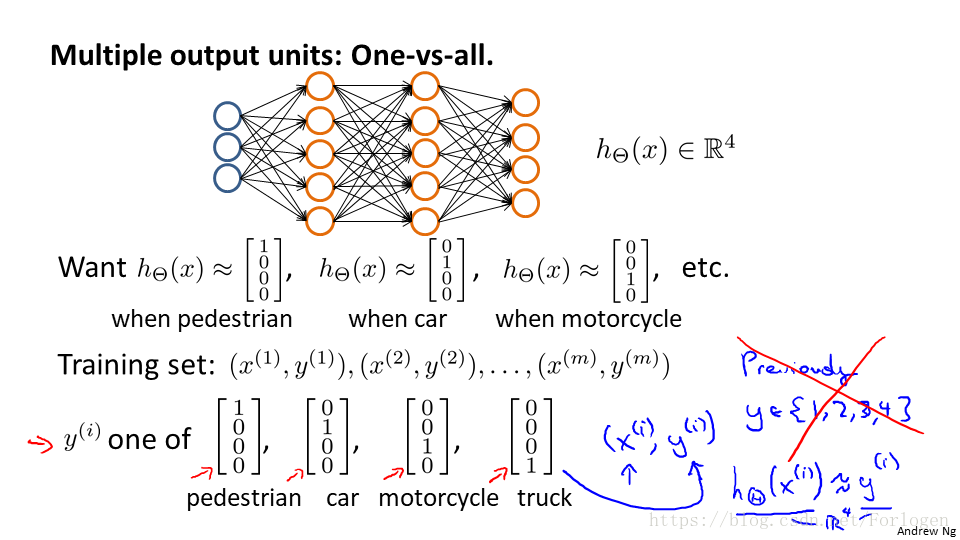
我們需要分四類，僅要給定四個輸出，判斷圖片中的是什麼，我們就使用不同的向量來表示不同的結果，而不再是使用簡單的不同的數字進行表示，具體的模型類似於這個：