cs231n （二）線性分類器

標籤（空格分隔）： 神經網路

0.回顧

cs231n （一）影象分類識別講了KNN

k-Nearest Neighbor分類器存在以下不足：

• 分類器必須記住所有訓練資料並將其儲存起來，以便於未來測試資料用於比較,儲存空間上是低效的.

• 對一個測試影象進行分類需要和所有訓練影象作比較，演算法計算資源耗費高。

1.線性分類

卷積神經網路: 主要有兩部分組成,

• 一個是評分函式（score function），它是原始影象資料到類別分值的對映,就是原資料啦!
• 另一個是損失函式（loss function），用來量化預測分類標籤的得分與真實標籤之間一致性的。該方法可轉化為一個最優化問題.

從影象到標籤分值的引數化對映

就是定義一個評分函式: 就是把影象量化,給電腦看.

線性分類器: 從最簡單的概率函式開始，一個線性對映 $f(x_i,W,b) = Wx_i + b$ 如果是CIFAR-10: $x_i:$ 3072x1, $W$: 10x3072, $b$: 10x1

• $W x_i $就可以有效地評估10個分類器，其中每個分類器是W的一行
• 訓練資料是用來學習到引數W和b的，一旦完成，就可以丟棄，留下學習到的引數.
• 只需要做一個矩陣乘法和一個矩陣加法就能對一個測試資料分類，這比k-NN中將測試影象和所有訓練資料做比較的方法快.

理解線性分類器

線性分類器: 影象中3個顏色通道中所有畫素的值與權重的矩陣乘，從而得到分類分值。

根據我們對權重設定的值，對於影象中的某些位置的某些顏色，函式表現出喜好或者厭惡.

舉個例子，想象“船”:就是被大量的藍色所包圍（對應的就是水）。

那麼“船”分類器在藍色通道上的權重就有很多的正權重，而在綠色和紅色通道上的權重為負的就比較多.

假設影象只有4個畫素（都是黑白畫素，這裡不考慮RGB通道），有3個分類（紅色代表貓，綠色代表狗，藍色代表船，注意，這裡的紅、綠和藍3種顏色僅代表分類，和RGB通道沒有關係）。

首先將影象畫素拉伸為一個列向量，與W進行矩陣乘，然後得到各個分類的分值。

需要注意的是，這個W一點也不好：貓分類的分值非常低。從上圖來看，演算法倒是覺得這個影象是一隻狗

將影象看作是高緯度的點: 每張影象是3072維空間中一個點,整個資料集就是一個點的集合，每個點都帶有1個分類標籤.(看圖)

假設把這些維度擠壓到二維，那麼就可以看看這些分類器在做了啥：

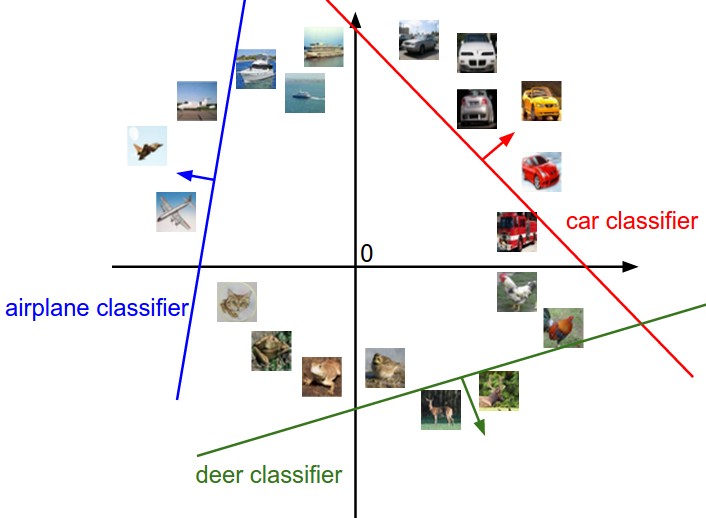
從上面可以看到，W的每一行都是一個分類類別的分類器。 對於這些數字的幾何解釋是：如果改變其中一行的數字，會看見分類器在空間中對應的直線開始向著不同方向旋轉。

而偏差b，則允許分類器對應的直線平移, 如果沒有偏差，無論權重如何，在x_i=0時分類分值始終為0。這樣所有分類器的線都必須穿過原點。

將線性分類器看做模板匹配: 我們沒有使用所有的訓練集的影象來比較，而是每個類別只用了一張圖片（這張圖片是我們學習到的，而不是訓練集中的某一張），我們會使用內積來計算向量間的距離，而不是使用L1或者L2距離。

這裡展示的是以CIFAR-10為訓練集，學習後的權重的例子。

船的模板確實有很多藍畫素, 如果影象是一艘船行駛在大海上，那麼這個模板利用內積計算影象將給出很高的分數.

偏差和權重的合併技巧:

以CIFAR-10為例，那麼$x_i$的大小就變成[3073x1]，不是[3072x1]了，多出了包含常量1的1個維度） W大小就是[10x3073]了, W中多出來的這一列對應的就是偏差值b，看圖!

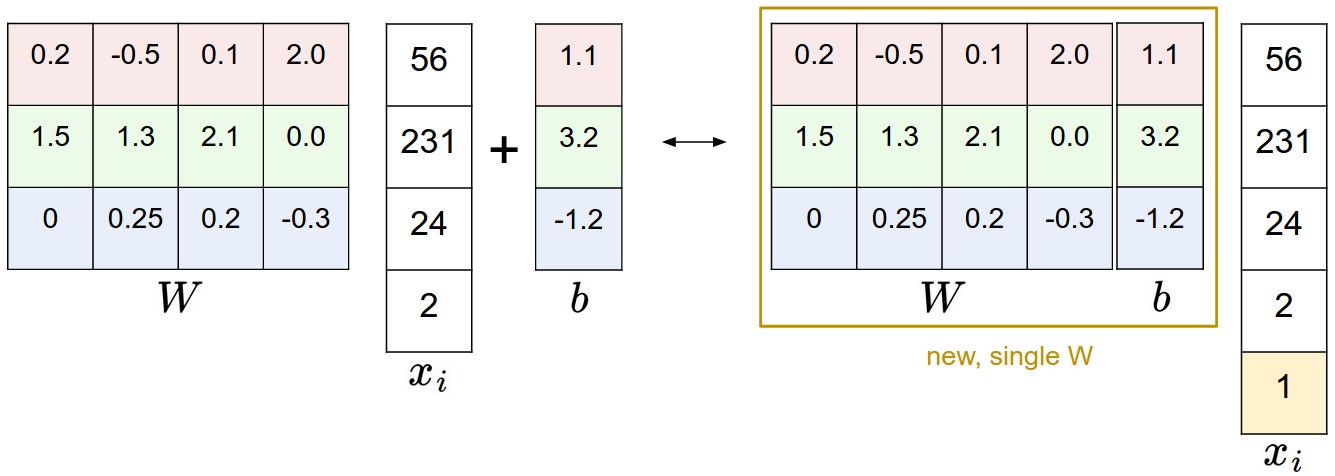
1. 左邊是先做矩陣乘法然後做加法
2. 右邊是將輸入向量的維度增加1個1的維度，在權重矩陣中增加一個偏差列b，最後做一個矩陣乘法. 這樣只需要學習一個權重矩陣,不用學W和b了.

影象資料預處理: 之前是0-255,現在對於輸入的特徵做歸一化,對每個特徵減去平均值來中心化資料很重要,即讓數值分佈區間變為[-1, 1]。零均值的中心化是很重要的,我們先了解梯度下降.

損失函式

評分函式搞定了,看看損失函式,其實就是看實際分數和已知分數的差越小越好, 聰明,就是零最好!

2.支援向量機(SVM)

先看看SVM的損失函式: 那麼第i個數據損失的定義就是

$\to L_i= \sum_{j\neq y_i}max(0, s_j-s_{y_i}+\Delta)$

具體如何計算,這個說的很清楚啦!

對於線性模型,評分函式是 $f(x_i, W) = W_{x_i}$, 那麼損失函式就是: $L_i = \sum_{j\neq y_i}max(0, w_j^T x_i - w_{y_i}^T x_i + \Delta)$

關於零閾值: max(0, -)函式, 也叫折葉損失, 那麼平方折葉損失SVM, 就是: (L2 -SVM), 也就是$max(0,-)_2$

**正則化（Regularization)?*不知道你看出來上面損失函式的問題了嗎,反正我是沒有(haha.gif)

我們需要懲罰一下這個權重W, 方法: 正則化懲罰, $R(W)=\sum_{k} \sum_{l} W_{k,l}^2$

那麼我們有: $L = \frac {1}{N}\sum_{j\neq y_i}max(0, w_j^T x_i - w_{y_i}^T x_i + \Delta) + \lambda \sum_{k} \sum_{l} W_{k,l}^2$

N是訓練集的資料量,最好對大數值權重進行懲罰，能提升其泛化能力，因為剔除能獨自對整體score有太大的影響的維度.

Code:無正則化部分的損失函式的Python實現，非向量化和半向量化兩種

def L_i(x, y, W):
  """
  unvectorized version. Compute the multiclass svm loss for a single example (x,y)
  - x is a column vector representing an image (e.g. 3073 x 1 in CIFAR-10)
    with an appended bias dimension in the 3073-rd position (i.e. bias trick)
  - y is an integer giving index of correct class (e.g. between 0 and 9 in CIFAR-10)
  - W is the weight matrix (e.g. 10 x 3073 in CIFAR-10)
  """
  delta = 1.0 # see notes about delta later in this section
  scores = W.dot(x) # scores becomes of size 10 x 1, the scores for each class
  correct_class_score = scores[y]
  D = W.shape[0] # number of classes, e.g. 10
  loss_i = 0.0
  for j in xrange(D): # iterate over all wrong classes
    if j == y:
      # skip for the true class to only loop over incorrect classes
      continue
    # accumulate loss for the i-th example
    loss_i += max(0, scores[j] - correct_class_score + delta)
  return loss_i

def L_i_vectorized(x, y, W):
  """
  A faster half-vectorized implementation. half-vectorized
  refers to the fact that for a single example the implementation contains
  no for loops, but there is still one loop over the examples (outside this function)
  """
  delta = 1.0
  scores = W.dot(x)
  # compute the margins for all classes in one vector operation
  margins = np.maximum(0, scores - scores[y] + delta)
  # on y-th position scores[y] - scores[y] canceled and gave delta. We want
  # to ignore the y-th position and only consider margin on max wrong class
  margins[y] = 0
  loss_i = np.sum(margins)
  return loss_i

def L(X, y, W):
  """
  fully-vectorized implementation :
  - X holds all the training examples as columns (e.g. 3073 x 50,000 in CIFAR-10)
  - y is array of integers specifying correct class (e.g. 50,000-D array)
  - W are weights (e.g. 10 x 3073)
  """
  # evaluate loss over all examples in X without using any for loops
  # left as exercise to reader in the assignment

實際考量

超引數 $\Delta$ 的選取: 該超引數在絕大多數情況下設為$\Delta=1.0$都是安全的。超引數$\Delta$和$\lambda$看起來是兩個不同的超引數，

實際上他們一起控制同一個權衡：即損失函式中的資料損失和正則化損失之間的權衡

梯度計算 在訓練過程中，我們需要通過最優化方法來是代價函式的損失值達到儘可能的小，所以我們對代價函式進行微分，然後計算其偏導數，得到以下公式 $\Delta_{w_i}L_i = 1(w_j^T x_i - w_{y_i}^T x_i + \Delta>0) x_i$ 對於每一個訓練樣本，我們計算它在每個分類上的得分，每當它在某一分類產生了損失（即scores[y[!i] - scores[y[i]] + delta > 0），那麼我們就將該分類上的引數梯度+Xi

3.Softmax分類器

它也很常見,它的損失函式肯定和SVM不一樣啊! 親愛的小傻瓜.

和SVM不同，Softmax的輸出啊（歸一化的分類概率）更加直觀，並且從概率上可以證明.

在Softmax分類器中，函式對映$f(x_i;W)=Wx_i$保持不變,並且將折葉損失（hinge loss）替換為交叉熵損失（cross-entropy loss）.

$\displaystyle Li=-log(\frac{e^{f_{y_i}}}{\sum_je^{f_j}})$ 或等價的$L_i=-f_{y_i}+log(\sum_je^{f_j})$

在上式中，使用$f_j$來表示分類評分向量f中的第j個元素, 其中函式$f_j(z)=\frac{e^{z_j}}{\sum_ke^{z_k}}$被稱作softmax 函式.

重mei點yong:

資訊理論視角：在“真實”分佈p和估計分佈q之間的交叉熵定義如下

$\displaystyle H(p,q)=-\sum_xp(x) logq(x)$

相關推薦