(轉載)深度學習基礎(3)——神經網路和反向傳播演算法
原文地址:https://www.zybuluo.com/hanbingtao/note/476663
轉載在此的目的是自己做個筆記,日後好複習,如侵權請聯絡我!!
在上一篇文章中,我們已經掌握了機器學習的基本套路,對模型、目標函式、優化演算法這些概念有了一定程度的理解,而且已經會訓練單個的感知器或者線性單元了。在這篇文章中,我們將把這些單獨的單元按照一定的規則相互連線在一起形成神經網路,從而奇蹟般的獲得了強大的學習能力。我們還將介紹這種網路的訓練演算法:反向傳播演算法。最後,我們依然用程式碼實現一個神經網路。如果您能堅持到本文的結尾,將會看到我們用自己實現的神經網路去識別手寫數字。現在請做好準備,您即將雙手觸及到深度學習的大門。
神經元
神經元和感知器本質上是一樣的,只不過我們說感知器的時候,它的啟用函式是階躍函式;而當我們說神經元的時候,啟用函式往往選擇為sigmoid函式或者tanh函式,如下圖所示:
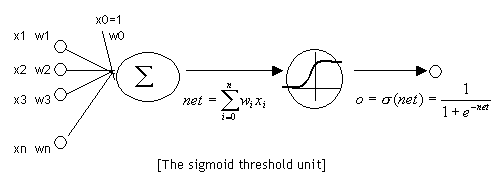

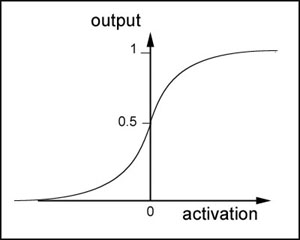
sigmoid函式是一個非線性函式,值域是(0,1)。函式影象如下圖所示:
sigmoid函式的導數是:

可以看到,sigmoid函式的導數非常有趣,它可以用sigmoid函式自身來表示。這樣,一旦計算出sigmoid函式的值,計算它的導數的值就非常方便。
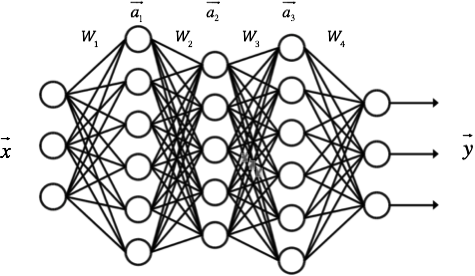
神經網路是什麼
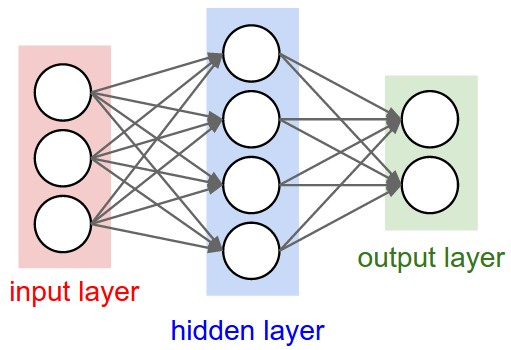
神經網路其實就是按照一定規則連線起來的多個神經元。上圖展示了一個全連線(full connected, FC)
- 神經元按照層來佈局。最左邊的層叫做輸入層,負責接收輸入資料;最右邊的層叫輸出層,我們可以從這層獲取神經網路輸出資料。輸入層和輸出層之間的層叫做隱藏層,因為它們對於外部來說是不可見的。
- 同一層的神經元之間沒有連線。
- 第N層的每個神經元和第N-1層的所有神經元相連(這就是full connected的含義),第N-1層神經元的輸出就是第N層神經元的輸入。
- 每個連線都有一個權值。
上面這些規則定義了全連線神經網路的結構。事實上還存在很多其它結構的神經網路,比如卷積神經網路(CNN)、迴圈神經網路(RNN),他們都具有不同的連線規則。
計算神經網路的輸出

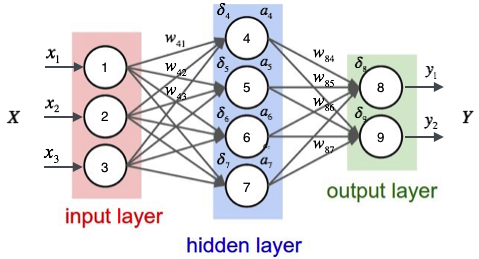
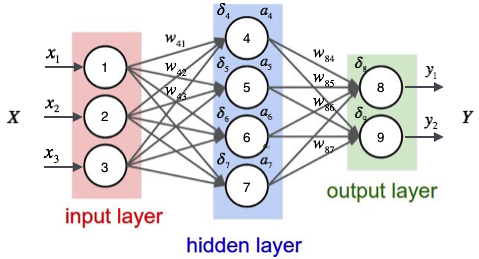
接下來,舉一個例子來說明這個過程,我們先給神經網路的每個單元寫上編號。
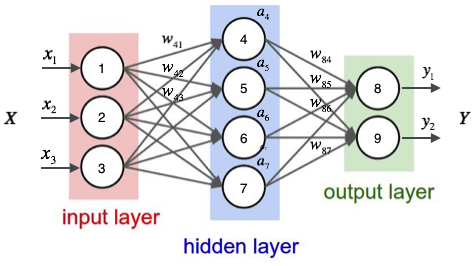
如上圖,輸入層有三個節點,我們將其依次編號為1、2、3;隱藏層的4個節點,編號依次為4、5、6、7;最後輸出層的兩個節點編號為8、9。因為我們這個神經網路是全連線網路,所以可以看到每個節點都和上一層的所有節點有連線。比如,我們可以看到隱藏層的節點4,它和輸入層的三個節點1、2、3之間都有連線,其連線上的權重分別為W41,W42,W43。那麼,我們怎樣計算節點4的輸出值a4呢?

神經網路的矩陣表示
神經網路的計算如果用矩陣來表示會很方便(當然逼格也更高),我們先來看看隱藏層的矩陣表示。
首先我們把隱藏層4個節點的計算依次排列出來:
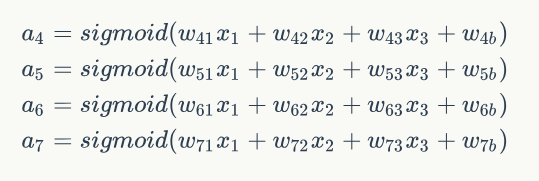



則最後一層的輸出向量的計算可以表示為:

這就是神經網路輸出值的計算方法。
神經網路的訓練
現在,我們需要知道一個神經網路的每個連線上的權值是如何得到的。我們可以說神經網路是一個模型,那麼這些權值就是模型的引數,也就是模型要學習的東西。然而,一個神經網路的連線方式、網路的層數、每層的節點數這些引數,則不是學習出來的,而是人為事先設定的。對於這些人為設定的引數,我們稱之為超引數(Hyper-Parameters)。
接下來,我們將要介紹神經網路的訓練演算法:反向傳播演算法。
反向傳播演算法(Back Propagation)
我們首先直觀的介紹反向傳播演算法,最後再來介紹這個演算法的推導。當然讀者也可以完全跳過推導部分,因為即使不知道如何推導,也不影響你寫出來一個神經網路的訓練程式碼。事實上,現在神經網路成熟的開源實現多如牛毛,除了練手之外,你可能都沒有機會需要去寫一個神經網路。
![]()


我們已經介紹了神經網路每個節點誤差項的計算和權重更新方法。顯然,計算一個節點的誤差項,需要先計算每個與其相連的下一層節點的誤差項。這就要求誤差項的計算順序必須是從輸出層開始,然後反向依次計算每個隱藏層的誤差項,直到與輸入層相連的那個隱藏層。這就是反向傳播演算法的名字的含義。當所有節點的誤差項計算完畢後,我們就可以根據式5來更新所有的權重。
以上就是基本的反向傳播演算法,並不是很複雜,您弄清楚了麼?
反向傳播演算法的推導
反向傳播演算法其實就是鏈式求導法則的應用。然而,這個如此簡單且顯而易見的方法,卻是在Roseblatt提出感知器演算法將近30年之後才被髮明和普及的。對此,Bengio這樣迴應道:
很多看似顯而易見的想法只有在事後才變得顯而易見。
接下來,我們用鏈式求導法則來推導反向傳播演算法,也就是上一小節的式3、式4、式5。
按照機器學習的通用套路,我們先確定神經網路的目標函式,然後用隨機梯度下降優化演算法去求目標函式最小值時的引數值。
我們取網路所有輸出層節點的誤差平方和作為目標函式:
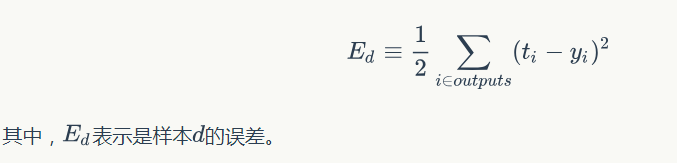
然後我們利用隨機梯度下降演算法對目標函式進行優化
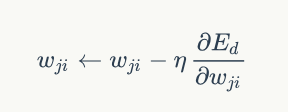
隨機梯度下降演算法也就是需要求出誤差Ed對於每個權重Wji的偏導數(也就是梯度)

輸出層權值訓練


隱藏層權值訓練

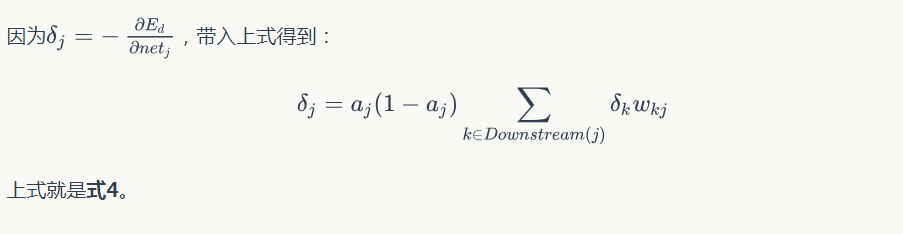
至此,我們已經推匯出了反向傳播演算法。需要注意的是,我們剛剛推匯出的訓練規則是根據啟用函式是sigmoid函式、平方和誤差、全連線網路、隨機梯度下降優化演算法。如果啟用函式不同、誤差計算方式不同、網路連線結構不同、優化演算法不同,則具體的訓練規則也會不一樣。但是無論怎樣,訓練規則的推導方式都是一樣的,應用鏈式求導法則進行推導即可。
神經網路的實現
現在,我們要根據前面的演算法,實現一個基本的全連線神經網路,這並不需要太多程式碼。我們在這裡依然採用面向物件設計。
首先,我們先做一個基本的模型:
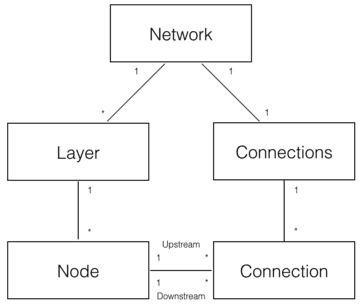
如上圖,可以分解出5個領域物件來實現神經網路:
- Network 神經網路物件,提供API介面。它由若干層物件組成以及連線物件組成。
- Layer 層物件,由多個節點組成。
- Node 節點物件計算和記錄節點自身的資訊(比如輸出值、誤差項等),以及與這個節點相關的上下游的連線。
- Connection 每個連線物件都要記錄該連線的權重。
- Connections 僅僅作為Connection的集合物件,提供一些集合操作。
Node實現如下:
# 節點類,負責記錄和維護節點自身資訊以及與這個節點相關的上下游連線,實現輸出值和誤差項的計算。
class Node(object):
def __init__(self, layer_index, node_index):
'''
構造節點物件。
layer_index: 節點所屬的層的編號
node_index: 節點的編號
'''
self.layer_index = layer_index
self.node_index = node_index
self.downstream = []
self.upstream = []
self.output = 0
self.delta = 0
def set_output(self, output):
'''
設定節點的輸出值。如果節點屬於輸入層會用到這個函式。
'''
self.output = output
def append_downstream_connection(self, conn):
'''
新增一個到下游節點的連線
'''
self.downstream.append(conn)
def append_upstream_connection(self, conn):
'''
新增一個到上游節點的連線
'''
self.upstream.append(conn)
def calc_output(self):
'''
根據式1計算節點的輸出
'''
output = reduce(lambda ret, conn: ret + conn.upstream_node.output * conn.weight, self.upstream, 0)
self.output = sigmoid(output)
def calc_hidden_layer_delta(self):
'''
節點屬於隱藏層時,根據式4計算delta
'''
downstream_delta = reduce(
lambda ret, conn: ret + conn.downstream_node.delta * conn.weight,
self.downstream, 0.0)
self.delta = self.output * (1 - self.output) * downstream_delta
def calc_output_layer_delta(self, label):
'''
節點屬於輸出層時,根據式3計算delta
'''
self.delta = self.output * (1 - self.output) * (label - self.output)
def __str__(self):
'''
列印節點的資訊
'''
node_str = '%u-%u: output: %f delta: %f' % (self.layer_index, self.node_index, self.output, self.delta)
downstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.downstream, '')
upstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.upstream, '')
return node_str + '\n\tdownstream:' + downstream_str + '\n\tupstream:' + upstream_str
constNode物件,為了實現一個輸出恆為1的節點(計算偏置項Wb時需要)
class ConstNode(object):
def __init__(self, layer_index, node_index):
'''
構造節點物件。
layer_index: 節點所屬的層的編號
node_index: 節點的編號
'''
self.layer_index = layer_index
self.node_index = node_index
self.downstream = []
self.output = 1
def append_downstream_connection(self, conn):
'''
新增一個到下游節點的連線
'''
self.downstream.append(conn)
def calc_hidden_layer_delta(self):
'''
節點屬於隱藏層時,根據式4計算delta
'''
downstream_delta = reduce(
lambda ret, conn: ret + conn.downstream_node.delta * conn.weight,
self.downstream, 0.0)
self.delta = self.output * (1 - self.output) * downstream_delta
def __str__(self):
'''
列印節點的資訊
'''
node_str = '%u-%u: output: 1' % (self.layer_index, self.node_index)
downstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.downstream, '')
return node_str + '\n\tdownstream:' + downstream_str
Layer物件,負責初始化一層。此外,作為Node的集合物件,提供對Node集合的操作。
class Layer(object):
def __init__(self, layer_index, node_count):
'''
初始化一層
layer_index: 層編號
node_count: 層所包含的節點個數
'''
self.layer_index = layer_index
self.nodes = []
for i in range(node_count):
self.nodes.append(Node(layer_index, i))
self.nodes.append(ConstNode(layer_index, node_count))
def set_output(self, data):
'''
設定層的輸出。當層是輸入層時會用到。
'''
for i in range(len(data)):
self.nodes[i].set_output(data[i])
def calc_output(self):
'''
計算層的輸出向量
'''
for node in self.nodes[:-1]:
node.calc_output()
def dump(self):
'''
列印層的資訊
'''
for node in self.nodes:
print node
Connection物件,主要職責是記錄連線的權重,以及這個連線所關聯的上下游節點。
class Connection(object):
def __init__(self, upstream_node, downstream_node):
'''
初始化連線,權重初始化為是一個很小的隨機數
upstream_node: 連線的上游節點
downstream_node: 連線的下游節點
'''
self.upstream_node = upstream_node
self.downstream_node = downstream_node
self.weight = random.uniform(-0.1, 0.1)
self.gradient = 0.0
def calc_gradient(self):
'''
計算梯度
'''
self.gradient = self.downstream_node.delta * self.upstream_node.output
def get_gradient(self):
'''
獲取當前的梯度
'''
return self.gradient
def update_weight(self, rate):
'''
根據梯度下降演算法更新權重
'''
self.calc_gradient()
self.weight += rate * self.gradient
def __str__(self):
'''
列印連線資訊
'''
return '(%u-%u) -> (%u-%u) = %f' % (
self.upstream_node.layer_index,
self.upstream_node.node_index,
self.downstream_node.layer_index,
self.downstream_node.node_index,
self.weight)
Connections物件,提供Connection集合操作。
class Connections(object):
def __init__(self):
self.connections = []
def add_connection(self, connection):
self.connections.append(connection)
def dump(self):
for conn in self.connections:
print conn
Network物件,提供API。
class Network(object):
def __init__(self, layers):
'''
初始化一個全連線神經網路
layers: 二維陣列,描述神經網路每層節點數
'''
self.connections = Connections()
self.layers = []
layer_count = len(layers)
node_count = 0;
for i in range(layer_count):
self.layers.append(Layer(i, layers[i]))
for layer in range(layer_count - 1):
connections = [Connection(upstream_node, downstream_node)
for upstream_node in self.layers[layer].nodes
for downstream_node in self.layers[layer + 1].nodes[:-1]]
for conn in connections:
self.connections.add_connection(conn)
conn.downstream_node.append_upstream_connection(conn)
conn.upstream_node.append_downstream_connection(conn)
def train(self, labels, data_set, rate, iteration):
'''
訓練神經網路
labels: 陣列,訓練樣本標籤。每個元素是一個樣本的標籤。
data_set: 二維陣列,訓練樣本特徵。每個元素是一個樣本的特徵。
'''
for i in range(iteration):
for d in range(len(data_set)):
self.train_one_sample(labels[d], data_set[d], rate)
def train_one_sample(self, label, sample, rate):
'''
內部函式,用一個樣本訓練網路
'''
self.predict(sample)
self.calc_delta(label)
self.update_weight(rate)
def calc_delta(self, label):
'''
內部函式,計算每個節點的delta
'''
output_nodes = self.layers[-1].nodes
for i in range(len(label)):
output_nodes[i].calc_output_layer_delta(label[i])
for layer in self.layers[-2::-1]:
for node in layer.nodes:
node.calc_hidden_layer_delta()
def update_weight(self, rate):
'''
內部函式,更新每個連線權重
'''
for layer in self.layers[:-1]:
for node in layer.nodes:
for conn in node.downstream:
conn.update_weight(rate)
def calc_gradient(self):
'''
內部函式,計算每個連線的梯度
'''
for layer in self.layers[:-1]:
for node in layer.nodes:
for conn in node.downstream:
conn.calc_gradient()
def get_gradient(self, label, sample):
'''
獲得網路在一個樣本下,每個連線上的梯度
label: 樣本標籤
sample: 樣本輸入
'''
self.predict(sample)
self.calc_delta(label)
self.calc_gradient()
def predict(self, sample):
'''
根據輸入的樣本預測輸出值
sample: 陣列,樣本的特徵,也就是網路的輸入向量
'''
self.layers[0].set_output(sample)
for i in range(1, len(self.layers)):
self.layers[i].calc_output()
return map(lambda node: node.output, self.layers[-1].nodes[:-1])
def dump(self):
'''
列印網路資訊
'''
for layer in self.layers:
layer.dump()
至此,實現了一個基本的全連線神經網路。可以看到,同神經網路的強大學習能力相比,其實現還算是很容易的。
梯度檢查
怎麼保證自己寫的神經網路沒有BUG呢?事實上這是一個非常重要的問題。一方面,千辛萬苦想到一個演算法,結果效果不理想,那麼是演算法本身錯了還是程式碼實現錯了呢?定位這種問題肯定要花費大量的時間和精力。另一方面,由於神經網路的複雜性,我們幾乎無法事先知道神經網路的輸入和輸出,因此類似TDD(測試驅動開發)這樣的開發方法似乎也不可行。
辦法還是有滴,就是利用梯度檢查來確認程式是否正確。梯度檢查的思路如下:
對於梯度下降演算法:


def gradient_check(network, sample_feature, sample_label):
'''
梯度檢查
network: 神經網路物件
sample_feature: 樣本的特徵
sample_label: 樣本的標籤
'''
# 計算網路誤差
network_error = lambda vec1, vec2: \
0.5 * reduce(lambda a, b: a + b,
map(lambda v: (v[0] - v[1]) * (v[0] - v[1]),
zip(vec1, vec2)))
# 獲取網路在當前樣本下每個連線的梯度
network.get_gradient(sample_feature, sample_label)
# 對每個權重做梯度檢查
for conn in network.connections.connections:
# 獲取指定連線的梯度
actual_gradient = conn.get_gradient()
# 增加一個很小的值,計算網路的誤差
epsilon = 0.0001
conn.weight += epsilon
error1 = network_error(network.predict(sample_feature), sample_label)
# 減去一個很小的值,計算網路的誤差
conn.weight -= 2 * epsilon # 剛才加過了一次,因此這裡需要減去2倍
error2 = network_error(network.predict(sample_feature), sample_label)
# 根據式6計算期望的梯度值
expected_gradient = (error2 - error1) / (2 * epsilon)
# 列印
print 'expected gradient: \t%f\nactual gradient: \t%f' % (
expected_gradient, actual_gradient)
至此,會推導、會實現、會抓BUG,你已經摸到深度學習的大門了。接下來還需要不斷的實踐,我們用剛剛寫過的神經網路去識別手寫數字。
神經網路實戰——手寫數字識別
可以參考部落格:https://www.cnblogs.com/wj-1314/p/9842719.html
針對這個任務,我們採用業界非常流行的MNIST資料集。MNIST大約有60000個手寫字母的訓練樣本,我們使用它訓練我們的神經網路,然後再用訓練好的網路去識別手寫數字。
手寫數字識別是個比較簡單的任務,數字只可能是0-9中的一個,這是個10分類問題。
程式碼實現:
首先,我們需要把MNIST資料集處理為神經網路能夠接受的形式。MNIST訓練集的檔案格式可以參考官方網站,這裡不在贅述。每個訓練樣本是一個28*28的影象,我們按照行優先,把它轉化為一個784維的向量。每個標籤是0-9的值,我們將其轉換為一個10維的one-hot向量:如果標籤值為n,我們就把向量的第維(從0開始編號)設定為0.9,而其它維設定為0.1。例如,向量[0.1,0.1,0.9,0.1,0.1,0.1,0.1,0.1,0.1,0.1]表示值2。
下面是處理MNIST資料的程式碼:
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
import struct
from bp import *
from datetime import datetime
# 資料載入器基類
class Loader(object):
def __init__(self, path, count):
'''
初始化載入器
path: 資料檔案路徑
count: 檔案中的樣本個數
'''
self.path = path
self.count = count
def get_file_content(self):
'''
讀取檔案內容
'''
f = open(self.path, 'rb')
content = f.read()
f.close()
return content
def to_int(self, byte):
'''
將unsigned byte字元轉換為整數
'''
return struct.unpack('B', byte)[0]
# 影象資料載入器
class ImageLoader(Loader):
def get_picture(self, content, index):
'''
內部函式,從檔案中獲取影象
'''
start = index * 28 * 28 + 16
picture = []
for i in range(28):
picture.append([])
for j in range(28):
picture[i].append(
self.to_int(content[start + i * 28 + j]))
return picture
def get_one_sample(self, picture):
'''
內部函式,將影象轉化為樣本的輸入向量
'''
sample = []
for i in range(28):
for j in range(28):
sample.append(picture[i][j])
return sample
def load(self):
'''
載入資料檔案,獲得全部樣本的輸入向量
'''
content = self.get_file_content()
data_set = []
for index in range(self.count):
data_set.append(
self.get_one_sample(
self.get_picture(content, index)))
return data_set
# 標籤資料載入器
class LabelLoader(Loader):
def load(self):
'''
載入資料檔案,獲得全部樣本的標籤向量
'''
content = self.get_file_content()
labels = []
for index in range(self.count):
labels.append(self.norm(content[index + 8]))
return labels
def norm(self, label):
'''
內部函式,將一個值轉換為10維標籤向量
'''
label_vec = []
label_value = self.to_int(label)
for i in range(10):
if i == label_value:
label_vec.append(0.9)
else:
label_vec.append(0.1)
return label_vec
def get_training_data_set():
'''
獲得訓練資料集
'''
image_loader = ImageLoader('train-images-idx3-ubyte', 60000)
label_loader = LabelLoader('train-labels-idx1-ubyte', 60000)
return image_loader.load(), label_loader.load()
def get_test_data_set():
'''
獲得測試資料集
'''
image_loader = ImageLoader('t10k-images-idx3-ubyte', 10000)
label_loader = LabelLoader('t10k-labels-idx1-ubyte', 10000)
return image_loader.load(), label_loader.load()
網路的輸出是一個10維向量,這個向量第n個(從0開始編號)元素的值最大,那麼n就是網路的識別結果。下面是程式碼實現:
def get_result(vec):
max_value_index = 0
max_value = 0
for i in range(len(vec)):
if vec[i] > max_value:
max_value = vec[i]
max_value_index = i
return max_value_index
我們使用錯誤率來對網路進行評估,下面是程式碼實現:
def evaluate(network, test_data_set, test_labels):
error = 0
total = len(test_data_set)
for i in range(total):
label = get_result(test_labels[i])
predict = get_result(network.predict(test_data_set[i]))
if label != predict:
error += 1
return float(error) / float(total)
最後實現我們的訓練策略:每訓練10輪,評估一次準確率,當準確率開始下降時終止訓練。下面是程式碼實現:
def train_and_evaluate():
last_error_ratio = 1.0
epoch = 0
train_data_set, train_labels = get_training_data_set()
test_data_set, test_labels = get_test_data_set()
network = Network([784, 300, 10])
while True:
epoch += 1
network.train(train_labels, train_data_set, 0.3, 1)
print '%s epoch %d finished' % (now(), epoch)
if epoch % 10 == 0:
error_ratio = evaluate(network, test_data_set, test_labels)
print '%s after epoch %d, error ratio is %f' % (now(), epoch, error_ratio)
if error_ratio > last_error_ratio:
break
else:
last_error_ratio = error_ratio
if __name__ == '__main__':
train_and_evaluate()
在我的機器上測試了一下,1個epoch大約需要9000多秒,所以要對程式碼做很多的效能優化工作(比如用向量化程式設計)。訓練要很久很久,可以把它上傳到伺服器上,在tmux的session裡面去執行。為了防止異常終止導致前功盡棄,我們每訓練10輪,就把獲得引數值儲存在磁碟上,以便後續可以恢復。(程式碼略)
向量化程式設計
在經歷了漫長的訓練之後,我們可能會想到,肯定有更好的辦法!是的,程式設計師們,現在我們需要告別面向物件程式設計了,轉而去使用另外一種更適合深度學習演算法的程式設計方式:向量化程式設計。主要有兩個原因:一個是我們事實上並不需要真的去定義Node、Connection這樣的物件,直接把數學計算實現了就可以了;另一個原因,是底層演算法庫會針對向量運算做優化(甚至有專用的硬體,比如GPU),程式效率會提升很多。所以,在深度學習的世界裡,我們總會想法設法的把計算表達為向量的形式。我相信優秀的程式設計師不會把自己拘泥於某種(自己熟悉的)程式設計正規化上,而會去學習並使用最為合適的正規化。
下面,我們用向量化程式設計的方法,重新實現前面的全連線神經網路。
首先,我們需要把所有的計算都表達為向量的形式。對於全連線神經網路來說,主要有三個計算公式。
前向計算,我們發現式2已經是向量化的表達了:

現在,我們根據上面幾個公式,重新實現一個類:FullConnectedLayer。它實現了全連線層的前向和後向計算:
# 全連線層實現類
class FullConnectedLayer(object):
def __init__(self, input_size, output_size,
activator):
'''
建構函式
input_size: 本層輸入向量的維度
output_size: 本層輸出向量的維度
activator: 啟用函式
'''
self.input_size = input_size
self.output_size = output_size
self.activator = activator
# 權重陣列W
self.W = np.random.uniform(-0.1, 0.1,
(output_size, input_size))
# 偏置項b
self.b = np.zeros((output_size, 1))
# 輸出向量
self.output = np.zeros((output_size, 1))
def forward(self, input_array):
'''
前向計算
input_array: 輸入向量,維度必須等於input_size
'''
# 式2
self.input = input_array
self.output = self.activator.forward(
np.dot(self.W, input_array) + self.b)
def backward(self, delta_array):
'''
反向計算W和b的梯度
delta_array: 從上一層傳遞過來的誤差項
'''
# 式8
self.delta = self.activator.backward(self.input) * np.dot(
self.W.T, delta_array)
self.W_grad = np.dot(delta_array, self.input.T)
self.b_grad = delta_array
def update(self, learning_rate):
'''
使用梯度下降演算法更新權重
'''
self.W += learning_rate * self.W_grad
self.b += learning_rate * self.b_grad
上面這個類一舉取代了原先的Layer、Node、Connection等類,不但程式碼更加容易理解,而且執行速度也快了幾百倍。
現在,我們對Network類稍作修改,使之用到FullConnectedLayer:
# Sigmoid啟用函式類
class SigmoidActivator(object):
def forward(self, weighted_input):
return 1.0 / (1.0 + np.exp(-weighted_input))
def backward(self, output):
return output * (1 - output)
# 神經網路類
class Network(object):
def __init__(self, layers):
'''
建構函式
'''
self.layers = []
for i in range(len(layers) - 1):
self.layers.append(
FullConnectedLayer(
layers[i], layers[i+1],
SigmoidActivator()
)
)
def predict(self, sample):
'''
使用神經網路實現預測
sample: 輸入樣本
'''
output = sample
for layer in self.layers:
layer.forward(output)
output = layer.output
return output
def train(self, labels, data_set, rate, epoch):
'''
訓練函式
labels: 樣本標籤
data_set: 輸入樣本
rate: 學習速率
epoch: 訓練輪數
'''
for i in range(epoch):
for d in range(len(data_set)):
self.train_one_sample(labels[d],
data_set[d], rate)
def train_one_sample(self, label, sample, rate):
self.predict(sample)
self.calc_gradient(label)
self.update_weight(rate)
def calc_gradient(self, label):
delta = self.layers[-1].activator.backward(
self.layers[-1].output
) * (label - self.layers[-1].output)
for layer in self.layers[::-1]:
layer.backward(delta)
delta = layer.delta
return delta
def update_weight(self, rate):
for layer in self.layers:
layer.update(rate)
現在,Network類也清爽多了,用我們的新程式碼再次訓練一下MNIST資料集吧。
小結
至此,你已經完成了又一次漫長的學習之旅。你現在應該已經明白了神經網路的基本原理,高興的話,你甚至有能力去動手實現一個,並用它解決一些問題。如果感到困難也不要氣餒,這篇文章是一個重要的分水嶺,如果你完全弄明白了的話,在真正的『小白』和裝腔作勢的『大牛』面前吹吹牛是完全沒有問題的。
作為深度學習入門的系列文章,本文也是上半場的結束。在這個半場,你掌握了機器學習、神經網路的基本概念,並且有能力去動手解決一些簡單的問題(例如手寫數字識別,如果用傳統的觀點來看,其實這些問題也不簡單)。而且,一旦掌握基本概念,後面的學習就容易多了。
在下半場,我們講介紹更多『深度』學習的內容,我們已經講了神經網路(Neutrol Network),但是並沒有講深度神經網路(Deep Neutrol Network)。Deep會帶來更加強大的能力,同時也帶來更多的問題。如果不理解這些問題和它們的解決方案,也不能說你入門了『深度』學習。
目前業界有很多開源的神經網路實現,它們的功能也要強大的多,因此你並不需要事必躬親的去實現自己的神經網路。我們在上半場不斷的從頭髮明輪子,是為了讓你明白神經網路的基本原理,這樣你就能非常迅速的掌握這些工具。在下半場的文章中,我們改變了策略:不會再去從頭開始去實現,而是儘可能應用現有的工具。
下一篇文章,我們介紹不同結構的神經網路,比如鼎鼎大名的卷積神經網路,它在影象和語音領域已然創造了諸多奇蹟,在自然語言處理領域的研究也如火如荼。某種意義上說,它的成功大大提升了人們對於深度學習的信心。
