機器學習入門二 ----- 機器學習術語表
機器學習術語表
本術語表中列出了一般的機器學習術語和 TensorFlow 專用術語的定義。
A
A/B 測試 (A/B testing)
一種統計方法,用於將兩種或多種技術進行比較,通常是將當前採用的技術與新技術進行比較。A/B 測試不僅旨在確定哪種技術的效果更好,而且還有助於瞭解相應差異是否具有顯著的統計意義。A/B 測試通常是採用一種衡量方式對兩種技術進行比較,但也適用於任意有限數量的技術和衡量方式。
準確率 (accuracy)
分類模型的正確預測所佔的比例。在多類別分類中,準確率的定義如下:
準確率正確的預測數樣本總數準確率=正確的預測數樣本總數
在二元分類中,準確率的定義如下:
準確率正例數負例數樣本總數準確率=正例數+負例數樣本總數
啟用函式 (activation function)
一種函式(例如 ReLU 或 S 型函式),用於對上一層的所有輸入求加權和,然後生成一個輸出值(通常為非線性值),並將其傳遞給下一層。
AdaGrad
一種先進的梯度下降法,用於重新調整每個引數的梯度,以便有效地為每個引數指定獨立的學習速率。如需檢視完整的解釋,請參閱這篇論文。
ROC 曲線下面積 (AUC, Area under the ROC Curve)
一種會考慮所有可能分類閾值的評估指標。
ROC 曲線下面積是,對於隨機選擇的正類別樣本確實為正類別,以及隨機選擇的負類別樣本為正類別,分類器更確信前者的概率。
B
反向傳播演算法 (backpropagation)
在神經網路上執行梯度下降法的主要演算法。該演算法會先按前向傳播方式計算(並快取)每個節點的輸出值,然後再按反向傳播遍歷圖的方式計算損失函式值相對於每個引數的偏導數。
基準 (baseline)
一種簡單的模型或啟發法,用作比較模型效果時的參考點。基準有助於模型開發者針對特定問題量化最低預期效果。
批次 (batch)
另請參閱批次大小。
批次大小 (batch size)
一個批次中的樣本數。例如,SGD 的批次大小為 1,而小批次的大小通常介於 10 到 1000 之間。批次大小在訓練和推斷期間通常是固定的;不過,TensorFlow 允許使用動態批次大小。
偏差 (bias)
距離原點的截距或偏移。偏差(也稱為偏差項)在機器學習模型中用 b 或 w0 表示。例如,在下面的公式中,偏差為 b:
y′=b+w1x1+w2x2+…wnxn
請勿與預測偏差混淆。
二元分類 (binary classification)
一種分類任務,可輸出兩種互斥類別之一。例如,對電子郵件進行評估並輸出“垃圾郵件”或“非垃圾郵件”的機器學習模型就是一個二元分類器。
分箱 (binning)
請參閱分桶。
分桶 (bucketing)
將一個特徵(通常是連續特徵)轉換成多個二元特徵(稱為桶或箱),通常根據值區間進行轉換。例如,您可以將溫度區間分割為離散分箱,而不是將溫度表示成單個連續的浮點特徵。假設溫度資料可精確到小數點後一位,則可以將介於 0.0 到 15.0 度之間的所有溫度都歸入一個分箱,將介於 15.1 到 30.0 度之間的所有溫度歸入第二個分箱,並將介於 30.1 到 50.0 度之間的所有溫度歸入第三個分箱。
C
校準層 (calibration layer)
一種預測後調整,通常是為了降低預測偏差的影響。調整後的預測和概率應與觀察到的標籤集的分佈一致。
候選取樣 (candidate sampling)
一種訓練時進行的優化,會使用某種函式(例如 softmax)針對所有正類別標籤計算概率,但對於負類別標籤,則僅針對其隨機樣本計算概率。例如,如果某個樣本的標籤為“小獵犬”和“狗”,則候選取樣將針對“小獵犬”和“狗”類別輸出以及其他類別(貓、棒棒糖、柵欄)的隨機子集計算預測概率和相應的損失項。這種取樣基於的想法是,只要正類別始終得到適當的正增強,負類別就可以從頻率較低的負增強中進行學習,這確實是在實際中觀察到的情況。候選取樣的目的是,通過不針對所有負類別計算預測結果來提高計算效率。
分類資料 (categorical data)
一種特徵,擁有一組離散的可能值。以某個名為 house style 的分類特徵為例,該特徵擁有一組離散的可能值(共三個),即 Tudor, ranch, colonial。通過將 house style 表示成分類資料,相應模型可以學習 Tudor、ranch 和 colonial 分別對房價的影響。
有時,離散集中的值是互斥的,只能將其中一個值應用於指定樣本。例如,car maker 分類特徵可能只允許一個樣本有一個值 (Toyota)。在其他情況下,則可以應用多個值。一輛車可能會被噴塗多種不同的顏色,因此,car color 分類特徵可能會允許單個樣本具有多個值(例如 red 和 white)。
分類特徵有時稱為離散特徵。
與數值資料相對。
形心 (centroid)
聚類的中心,由 k-means 或 k-median 演算法決定。例如,如果 k 為 3,則 k-means 或 k-median 演算法會找出 3 個形心。
檢查點 (checkpoint)
一種資料,用於捕獲模型變數在特定時間的狀態。藉助檢查點,可以匯出模型權重,跨多個會話執行訓練,以及使訓練在發生錯誤之後得以繼續(例如作業搶佔)。請注意,圖本身不包含在檢查點中。
類別 (class)
為標籤列舉的一組目標值中的一個。例如,在檢測垃圾郵件的二元分類模型中,兩種類別分別是“垃圾郵件”和“非垃圾郵件”。在識別狗品種的多類別分類模型中,類別可以是“貴賓犬”、“小獵犬”、“哈巴犬”等等。
分類不平衡的資料集 (class-imbalanced data set)
一種二元分類問題,在此類問題中,兩種類別的標籤在出現頻率方面具有很大的差距。例如,在某個疾病資料集中,0.0001 的樣本具有正類別標籤,0.9999 的樣本具有負類別標籤,這就屬於分類不平衡問題;但在某個足球比賽預測器中,0.51 的樣本的標籤為其中一個球隊贏,0.49 的樣本的標籤為另一個球隊贏,這就不屬於分類不平衡問題。
分類模型 (classification model)
一種機器學習模型,用於區分兩種或多種離散類別。例如,某個自然語言處理分類模型可以確定輸入的句子是法語、西班牙語還是義大利語。請與迴歸模型進行比較。
分類閾值 (classification threshold)
一種標量值條件,應用於模型預測的得分,旨在將正類別與負類別區分開。將邏輯迴歸結果對映到二元分類時使用。以某個邏輯迴歸模型為例,該模型用於確定指定電子郵件是垃圾郵件的概率。如果分類閾值為 0.9,那麼邏輯迴歸值高於 0.9 的電子郵件將被歸類為“垃圾郵件”,低於 0.9 的則被歸類為“非垃圾郵件”。
聚類 (clustering)
將關聯的樣本分成一組,一般用於非監督式學習。在所有樣本均分組完畢後,相關人員便可選擇性地為每個聚類賦予含義。
聚類演算法有很多。例如,k-means 演算法會基於樣本與形心的接近程度聚類樣本,如下圖所示:
樹高度樹寬度形心聚類 1聚類 2
之後,研究人員便可檢視這些聚類並進行其他操作,例如,將聚類 1 標記為“矮型樹”,將聚類 2 標記為“全尺寸樹”。
再舉一個例子,例如基於樣本與中心點距離的聚類演算法,如下所示:
聚類 1聚類 2聚類 3
協同過濾 (collaborative filtering)
根據很多其他使用者的興趣來預測某位使用者的興趣。協同過濾通常用在推薦系統中。
混淆矩陣 (confusion matrix)
一種 NxN 表格,用於總結分類模型的預測效果;即標籤和模型預測的分類之間的關聯。在混淆矩陣中,一個軸表示模型預測的標籤,另一個軸表示實際標籤。N 表示類別個數。在二元分類問題中,N=2。例如,下面顯示了一個二元分類問題的混淆矩陣示例:
| 腫瘤(預測的標籤) | 非腫瘤(預測的標籤) | |
|---|---|---|
| 腫瘤(實際標籤) | 18 | 1 |
| 非腫瘤(實際標籤) | 6 | 452 |
上面的混淆矩陣顯示,在 19 個實際有腫瘤的樣本中,該模型正確地將 18 個歸類為有腫瘤(18 個正例),錯誤地將 1 個歸類為沒有腫瘤(1 個假負例)。同樣,在 458 個實際沒有腫瘤的樣本中,模型歸類正確的有 452 個(452 個負例),歸類錯誤的有 6 個(6 個假正例)。
多類別分類問題的混淆矩陣有助於確定出錯模式。例如,某個混淆矩陣可以揭示,某個經過訓練以識別手寫數字的模型往往會將 4 錯誤地預測為 9,將 7 錯誤地預測為 1。
混淆矩陣包含計算各種效果指標(包括精確率和召回率)所需的充足資訊。
連續特徵 (continuous feature)
一種浮點特徵,可能值的區間不受限制。與離散特徵相對。
收斂 (convergence)
通俗來說,收斂通常是指在訓練期間達到的一種狀態,即經過一定次數的迭代之後,訓練損失和驗證損失在每次迭代中的變化都非常小或根本沒有變化。也就是說,如果採用當前資料進行額外的訓練將無法改進模型,模型即達到收斂狀態。在深度學習中,損失值有時會在最終下降之前的多次迭代中保持不變或幾乎保持不變,暫時形成收斂的假象。
另請參閱早停法。
另請參閱 Boyd 和 Vandenberghe 合著的 Convex Optimization(《凸優化》)。
凸函式 (convex function)
一種函式,函式影象以上的區域為凸集。典型凸函式的形狀類似於字母 U。例如,以下都是凸函式:

相反,以下函式則不是凸函式。請注意影象上方的區域如何不是凸集:
區域性最低點區域性最低點全域性最低點
嚴格凸函式只有一個區域性最低點,該點也是全域性最低點。經典的 U 形函式都是嚴格凸函式。不過,有些凸函式(例如直線)則不是這樣。
很多常見的損失函式(包括下列函式)都是凸函式:
梯度下降法的很多變體都一定能找到一個接近嚴格凸函式最小值的點。同樣,隨機梯度下降法的很多變體都有很高的可能效能夠找到接近嚴格凸函式最小值的點(但並非一定能找到)。
兩個凸函式的和(例如 L2 損失函式 + L1 正則化)也是凸函式。
深度模型絕不會是凸函式。值得注意的是,專門針對凸優化設計的演算法往往總能在深度網路上找到非常好的解決方案,雖然這些解決方案並不一定對應於全域性最小值。
凸優化 (convex optimization)
使用數學方法(例如梯度下降法)尋找凸函式最小值的過程。機器學習方面的大量研究都是專注於如何通過公式將各種問題表示成凸優化問題,以及如何更高效地解決這些問題。
如需完整的詳細資訊,請參閱 Boyd 和 Vandenberghe 合著的 Convex Optimization(《凸優化》)。
凸集 (convex set)
歐幾里得空間的一個子集,其中任意兩點之間的連線仍完全落在該子集內。例如,下面的兩個圖形都是凸集:

相反,下面的兩個圖形都不是凸集:

卷積 (convolution)
簡單來說,卷積在數學中指兩個函式的組合。在機器學習中,卷積結合使用卷積過濾器和輸入矩陣來訓練權重。
如果沒有卷積,機器學習演算法就需要學習大張量中每個單元格各自的權重。例如,用 2K x 2K 影象訓練的機器學習演算法將被迫找出 400 萬個單獨的權重。而使用卷積,機器學習演算法只需在卷積過濾器中找出每個單元格的權重,大大減少了訓練模型所需的記憶體。在應用卷積過濾器後,它只需跨單元格進行復制,每個單元格都會與過濾器相乘。
卷積過濾器 (convolutional filter)
卷積運算中的兩個參與方之一。(另一個參與方是輸入矩陣切片。)卷積過濾器是一種矩陣,其等級與輸入矩陣相同,但形狀小一些。以 28×28 的輸入矩陣為例,過濾器可以是小於 28×28 的任何二維矩陣。
在圖形操作中,卷積過濾器中的所有單元格通常按照固定模式設定為 1 和 0。在機器學習中,卷積過濾器通常先選擇隨機數字,然後由網路訓練出理想值。
卷積層 (convolutional layer)
深度神經網路的一個層,卷積過濾器會在其中傳遞輸入矩陣。以下面的 3x3 卷積過濾器為例:
下面的動畫顯示了一個由 9 個卷積運算(涉及 5x5 輸入矩陣)組成的卷積層。請注意,每個卷積運算都涉及一個不同的 3x3 輸入矩陣切片。由此產生的 3×3 矩陣(右側)就包含 9 個卷積運算的結果:
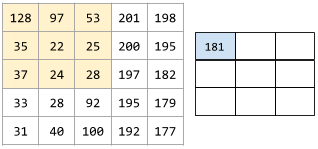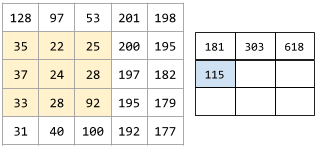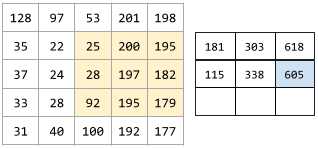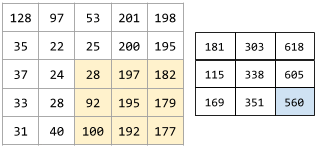
卷積神經網路 (convolutional neural network)
一種神經網路,其中至少有一層為卷積層。典型的卷積神經網路包含以下幾層的組合:
- 卷積層
- 池化層
- 密集層
卷積神經網路在解決某些型別的問題(如影象識別)上取得了巨大成功。
卷積運算 (convolutional operation)
如下所示的兩步數學運算:
- 對卷積過濾器和輸入矩陣切片執行元素級乘法。(輸入矩陣切片與卷積過濾器具有相同的等級和大小。)
- 對生成的積矩陣中的所有值求和。
以下面的 5x5 輸入矩陣為例:
現在,以下面這個 2x2 卷積過濾器為例:
每個卷積運算都涉及一個 2x2 輸入矩陣切片。例如,假設我們使用輸入矩陣左上角的 2x2 切片。這樣一來,對此切片進行卷積運算將如下所示:
卷積層由一系列卷積運算組成,每個卷積運算都針對不同的輸入矩陣切片。
成本 (cost)
與損失的含義相同。
交叉熵 (交叉熵-cross-entropy)
對數損失函式向多類別分類問題的一種泛化。交叉熵可以量化兩種概率分佈之間的差異。另請參閱困惑度。
自定義 Estimator (custom Estimator)
D
資料分析 (data analysis)
根據樣本、測量結果和視覺化內容來理解資料。資料分析在首次收到資料集、構建第一個模型之前特別有用。此外,資料分析在理解實驗和除錯系統問題方面也至關重要。
DataFrame
一種熱門的資料型別,用於表示 Pandas 中的資料集。DataFrame 類似於表格。DataFrame 的每一列都有一個名稱(標題),每一行都由一個數字標識。
資料集 (data set)
一組樣本的集合。
Dataset API (tf.data)
一種高級別的 TensorFlow API,用於讀取資料並將其轉換為機器學習演算法所需的格式。tf.data.Dataset 物件表示一系列元素,其中每個元素都包含一個或多個張量。tf.data.Iterator 物件可獲取 Dataset 中的元素。
如需詳細瞭解 Dataset API,請參閱《TensorFlow 程式設計人員指南》中的匯入資料。
決策邊界 (decision boundary)
在二元分類或多類別分類問題中,模型學到的類別之間的分界線。例如,在以下表示某個二元分類問題的圖片中,決策邊界是橙色類別和藍色類別之間的分界線:

密集層 (dense layer)
與全連線層的含義相同。
深度模型 (deep model)
一種神經網路,其中包含多個隱藏層。深度模型依賴於可訓練的非線性關係。
與寬度模型相對。
密集特徵 (dense feature)
一種大部分值是非零值的特徵,通常是浮點值張量。與稀疏特徵相對。
裝置 (device)
一類可執行 TensorFlow 會話的硬體,包括 CPU、GPU 和 TPU。
離散特徵 (discrete feature)
一種特徵,包含有限個可能值。例如,某個值只能是“動物”、“蔬菜”或“礦物”的特徵便是一個離散特徵(或分類特徵)。與連續特徵相對。
丟棄正則化 (dropout regularization)
正則化的一種形式,在訓練神經網路方面非常有用。丟棄正則化的運作機制是,在一個梯度步長中移除從神經網路層中隨機選擇的固定數量的單元。丟棄的單元越多,正則化效果就越強。這類似於訓練神經網路以模擬較小網路的指數級規模整合學習。如需完整的詳細資訊,請參閱 Dropout: A Simple Way to Prevent Neural Networks from Overfitting(《丟棄:一種防止神經網路過擬合的簡單方法》)。
動態模型 (dynamic model)
一種模型,以持續更新的方式線上接受訓練。也就是說,資料會源源不斷地進入這種模型。
E
早停法 (early stopping)
一種正則化方法,是指在訓練損失仍可以繼續降低之前結束模型訓練。使用早停法時,您會在驗證資料集的損失開始增大(也就是泛化效果變差)時結束模型訓練。
巢狀 (embeddings)
一種分類特徵,以連續值特徵表示。通常,巢狀是指將高維度向量對映到低維度的空間。例如,您可以採用以下兩種方式之一來表示英文句子中的單詞:
- 表示成包含百萬個元素(高維度)的稀疏向量,其中所有元素都是整數。向量中的每個單元格都表示一個單獨的英文單詞,單元格中的值表示相應單詞在句子中出現的次數。由於單個英文句子包含的單詞不太可能超過 50 個,因此向量中幾乎每個單元格都包含 0。少數非 0 的單元格中將包含一個非常小的整數(通常為 1),該整數表示相應單詞在句子中出現的次數。
- 表示成包含數百個元素(低維度)的密集向量,其中每個元素都儲存一個介於 0 到 1 之間的浮點值。這就是一種巢狀。
在 TensorFlow 中,會按反向傳播損失訓練巢狀,和訓練神經網路中的任何其他引數一樣。
經驗風險最小化 (ERM, empirical risk minimization)
用於選擇可以將基於訓練集的損失降至最低的函式。與結構風險最小化相對。
整合學習 (ensemble)
多個模型的預測結果的並集。您可以通過以下一項或多項來建立整合學習:
- 不同的初始化
- 不同的超引數
- 不同的整體結構
週期 (epoch)
在訓練時,整個資料集的一次完整遍歷,以便不漏掉任何一個樣本。因此,一個週期表示(N/批次大小)次訓練迭代,其中 N 是樣本總數。
Estimator
tf.Estimator 類的一個例項,用於封裝負責構建 TensorFlow 圖並執行 TensorFlow 會話的邏輯。您可以建立自定義 Estimator(如需相關介紹,請點選此處),也可以例項化其他人預建立的 Estimator。
樣本 (example)
資料集的一行。一個樣本包含一個或多個特徵,此外還可能包含一個標籤。另請參閱有標籤樣本和無標籤樣本。
F
假負例 (FN, false negative)
被模型錯誤地預測為負類別的樣本。例如,模型推斷出某封電子郵件不是垃圾郵件(負類別),但該電子郵件其實是垃圾郵件。
假正例 (FP, false positive)
被模型錯誤地預測為正類別的樣本。例如,模型推斷出某封電子郵件是垃圾郵件(正類別),但該電子郵件其實不是垃圾郵件。
假正例率(false positive rate, 簡稱 FP 率)
ROC 曲線中的 x 軸。FP 率的定義如下:
假正例率假正例數假正例數負例數假正例率=假正例數假正例數+負例數
特徵 (feature)
在進行預測時使用的輸入變數。
特徵列 (tf.feature_column)
指定模型應該如何解讀特定特徵的一種函式。此類函式的輸出結果是所有 Estimators 建構函式的必需引數。
藉助 tf.feature_column 函式,模型可對輸入特徵的不同表示法輕鬆進行實驗。有關詳情,請參閱《TensorFlow 程式設計人員指南》中的特徵列一章。
“特徵列”是 Google 專用的術語。特徵列在 Yahoo/Microsoft 使用的 VW 系統中稱為“名稱空間”,也稱為場。
特徵組合 (feature cross)
通過將單獨的特徵進行組合(求笛卡爾積)而形成的合成特徵。特徵組合有助於表達非線性關係。
特徵工程 (feature engineering)
指以下過程:確定哪些特徵可能在訓練模型方面非常有用,然後將日誌檔案及其他來源的原始資料轉換為所需的特徵。在 TensorFlow 中,特徵工程通常是指將原始日誌檔案條目轉換為 tf.Example 協議緩衝區。另請參閱 tf.Transform。
特徵工程有時稱為特徵提取。
特徵集 (feature set)
訓練機器學習模型時採用的一組特徵。例如,對於某個用於預測房價的模型,郵政編碼、房屋面積以及房屋狀況可以組成一個簡單的特徵集。
特徵規範 (feature spec)
用於描述如何從 tf.Example 協議緩衝區提取特徵資料。由於 tf.Example 協議緩衝區只是一個數據容器,因此您必須指定以下內容:
- 要提取的資料(即特徵的鍵)
- 資料型別(例如 float 或 int)
- 長度(固定或可變)
少量樣本學習 (few-shot learning)
一種機器學習方法(通常用於物件分類),旨在僅通過少量訓練樣本學習有效的分類器。
另請參閱單樣本學習。
完整 softmax (full softmax)
全連線層 (fully connected layer)
一種隱藏層,其中的每個節點均與下一個隱藏層中的每個節點相連。
全連線層又稱為密集層。
G
泛化 (generalization)
指的是模型依據訓練時採用的資料,針對以前未見過的新資料做出正確預測的能力。
廣義線性模型 (generalized linear model)
最小二乘迴歸模型(基於高斯噪聲)向其他型別的模型(基於其他型別的噪聲,例如泊松噪聲或分類噪聲)進行的一種泛化。廣義線性模型的示例包括:
- 邏輯迴歸
- 多類別迴歸
- 最小二乘迴歸
可以通過凸優化找到廣義線性模型的引數。
廣義線性模型具有以下特性:
- 最優的最小二乘迴歸模型的平均預測結果等於訓練資料的平均標籤。
- 最優的邏輯迴歸模型預測的平均概率等於訓練資料的平均標籤。
廣義線性模型的功能受其特徵的限制。與深度模型不同,廣義線性模型無法“學習新特徵”。
梯度 (gradient)
偏導數相對於所有自變數的向量。在機器學習中,梯度是模型函式偏導數的向量。梯度指向最高速上升的方向。
梯度裁剪 (gradient clipping)
在應用[梯度](http://wsccoder.top/2018/09/23/機器學習術語表/#梯度-gradient值之前先設定其上限。梯度裁剪有助於確保數值穩定性以及防止梯度爆炸。
梯度下降法 (gradient descent)
一種通過計算並且減小梯度將損失降至最低的技術,它以訓練資料為條件,來計算損失相對於模型引數的梯度。通俗來說,梯度下降法以迭代方式調整引數,逐漸找到權重和偏差的最佳組合,從而將損失降至最低。
圖 (graph)
TensorFlow 中的一種計算規範。圖中的節點表示操作。邊緣具有方向,表示將某項操作的結果(一個張量)作為一個運算元傳遞給另一項操作。可以使用 TensorBoard 直觀呈現圖。
H
啟發法 (heuristic)
一種非最優但實用的問題解決方案,足以用於進行改進或從中學習。
隱藏層 (hidden layer)
神經網路中的合成層,介於輸入層(即特徵)和輸出層(即預測)之間。神經網路包含一個或多個隱藏層。
合頁損失函式 (hinge loss)
一系列用於分類的損失函式,旨在找到距離每個訓練樣本都儘可能遠的決策邊界,從而使樣本和邊界之間的裕度最大化。KSVM 使用合頁損失函式(或相關函式,例如平方合頁損失函式)。對於二元分類,合頁損失函式的定義如下:
loss=max(0,1−(y′∗y))
其中“y’”表示分類器模型的原始輸出:
y′=b+w1x1+w2x2+…wnxn
“y”表示真標籤,值為 -1 或 +1。
因此,合頁損失與 (y * y’) 的關係圖如下所示:
0-2-112312340合頁損失函式(y * y’)
維持資料 (holdout data)
訓練期間故意不使用(“維持”)的樣本。驗證資料集和測試資料集都屬於維持資料。維持資料有助於評估模型向訓練時所用資料之外的資料進行泛化的能力。與基於訓練資料集的損失相比,基於維持資料集的損失有助於更好地估算基於未見過的資料集的損失。
超引數 (hyperparameter)
在模型訓練的連續過程中,您調節的“旋鈕”。例如,學習速率就是一種超引數。
與引數相對。
超平面 (hyperplane)
將一個空間劃分為兩個子空間的邊界。例如,在二維空間中,直線就是一個超平面,在三維空間中,平面則是一個超平面。在機器學習中更典型的是:超平面是分隔高維度空間的邊界。核支援向量機利用超平面將正類別和負類別區分開來(通常是在極高維度空間中)。
I
獨立同等分佈 (i.i.d, independently and identically distributed)
從不會改變的分佈中提取的資料,其中提取的每個值都不依賴於之前提取的值。i.i.d. 是機器學習的理想氣體 - 一種實用的數學結構,但在現實世界中幾乎從未發現過。例如,某個網頁的訪問者在短時間內的分佈可能為 i.i.d.,即分佈在該短時間內沒有變化,且一位使用者的訪問行為通常與另一位使用者的訪問行為無關。不過,如果將時間視窗擴大,網頁訪問者的分佈可能呈現出季節性變化。
推斷 (inference)
在機器學習中,推斷通常指以下過程:通過將訓練過的模型應用於無標籤樣本來做出預測。在統計學中,推斷是指在某些觀測資料條件下擬合分佈引數的過程。(請參閱維基百科中有關統計學推斷的文章。)
輸入函式 (input function)
在 TensorFlow 中,用於將輸入資料返回到 Estimator 的訓練、評估或預測方法的函式。例如,訓練輸入函式會返回訓練集中的一批特徵和標籤。
輸入層 (input layer)
神經網路中的第一層(接收輸入資料的層)。
例項 (instance)
與樣本的含義相同。
可解釋性 (interpretability)
模型的預測可解釋的難易程度。深度模型通常不可解釋,也就是說,很難對深度模型的不同層進行解釋。相比之下,線性迴歸模型和寬度模型的可解釋性通常要好得多。
評分者間一致性信度 (inter-rater agreement)
一種衡量指標,用於衡量在執行某項任務時評分者達成一致的頻率。如果評分者未達成一致,則可能需要改進任務說明。有時也稱為註釋者間一致性信度或評分者間可靠性信度。另請參閱 Cohen’s kappa(最熱門的評分者間一致性信度衡量指標之一)。
迭代 (iteration)
模型的權重在訓練期間的一次更新。迭代包含計算引數在單批次資料上的梯度損失。
K
k-means
一種熱門的聚類演算法,用於對非監督式學習中的樣本進行分組。k-means 演算法基本上會執行以下操作:
- 以迭代方式確定最佳的 k 中心點(稱為形心)。
- 將每個樣本分配到最近的形心。與同一個形心距離最近的樣本屬於同一個組。
k-means 演算法會挑選形心位置,以最大限度地減小每個樣本與其最接近形心之間的距離的累積平方。
以下面的小狗高度與小狗寬度的關係圖為例:
高度寬度
如果 k=3,則 k-means 演算法會確定三個形心。每個樣本都被分配到與其最接近的形心,最終產生三個組:
高度寬度形心聚類 1聚類 2聚類 3
假設製造商想要確定小、中和大號狗毛衣的理想尺寸。在該聚類中,三個形心用於標識每隻狗的平均高度和平均寬度。因此,製造商可能應該根據這三個形心確定毛衣尺寸。請注意,聚類的形心通常不是聚類中的樣本。
上圖顯示了 k-means 應用於僅具有兩個特徵(高度和寬度)的樣本。請注意,k-means 可以跨多個特徵為樣本分組。
k-median
與 k-means 緊密相關的聚類演算法。兩者的實際區別如下:
- 對於 k-means,確定形心的方法是,最大限度地減小候選形心與它的每個樣本之間的距離平方和。
- 對於 k-median,確定形心的方法是,最大限度地減小候選形心與它的每個樣本之間的距離總和。
請注意,距離的定義也有所不同:
- k-means 採用從形心到樣本的歐幾里得距離。(在二維空間中,歐幾里得距離即使用勾股定理來計算斜邊。)例如,(2,2) 與 (5,-2) 之間的 k-means 距離為:
歐幾里德距離歐幾里德距離=(2−5)2+(2−−2)2=5
- k-median 採用從形心到樣本的曼哈頓距離。這個距離是每個維度中絕對差異值的總和。例如,(2,2) 與 (5,-2) 之間的 k-median 距離為:
| 曼哈頓距離曼哈頓距離= | 2−5 | + | 2−−2 | =7 |
Keras
一種熱門的 Python 機器學習 API。Keras 能夠在多種深度學習框架上執行,其中包括 TensorFlow(在該框架上,Keras 作為 tf.keras 提供)。
核支援向量機 (KSVM, Kernel Support Vector Machines)
一種分類演算法,旨在通過將輸入資料向量對映到更高維度的空間,來最大化正類別和負類別之間的裕度。以某個輸入資料集包含一百個特徵的分類問題為例。為了最大化正類別和負類別之間的裕度,KSVM 可以在內部將這些特徵對映到百萬維度的空間。KSVM 使用合頁損失函式。
L
L1 損失函式 (L₁ loss)
一種損失函式,基於模型預測的值與標籤的實際值之差的絕對值。與 L2 損失函式相比,L1 損失函式對離群值的敏感性弱一些。
L1 正則化 (L₁ regularization)
一種正則化,根據權重的絕對值的總和來懲罰權重。在依賴稀疏特徵的模型中,L1 正則化有助於使不相關或幾乎不相關的特徵的權重正好為 0,從而將這些特徵從模型中移除。與 L2 正則化相對。
L2 損失函式 (L₂ loss)
L2 正則化 (L₂ regularization)
一種正則化,根據權重的平方和來懲罰權重。L2 正則化有助於使離群值(具有較大正值或較小負值)權重接近於 0,但又不正好為 0。(與 L1 正則化相對。)線上性模型中,L2 正則化始終可以改進泛化。
標籤 (label)
在監督式學習中,標籤指樣本的“答案”或“結果”部分。有標籤資料集中的每個樣本都包含一個或多個特徵以及一個標籤。例如,在房屋資料集中,特
