機器學習術語表——Beta

阿新 • • 發佈：2018-12-21

機器學習術語表 ^Beta

提示：你可以通過中文名稱拼音首字母快速檢索。

C

超引數｜Hyperparameter

在機器學習中，超引數是在開始學習過程之前設定值的引數，而不是通過訓練得到的引數資料。通常情況下，需要對超引數進行優化，給模型選擇一組最優超引數，以提高學習的效能和效果。

超平面｜Hyperplane

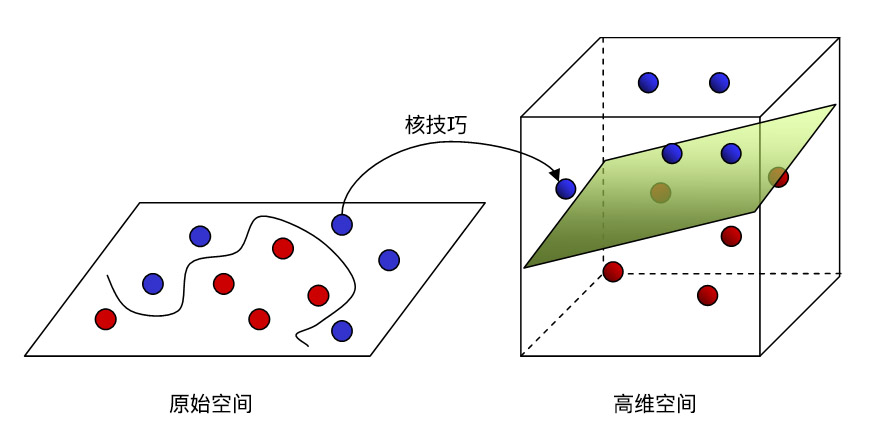
將一個空間劃分為兩個子空間的邊界。例如，在二維空間中，直線就是一個超平面，在三維空間中，平面則是一個超平面。在機器學習中更典型的是：超平面是分隔高維度空間的邊界。核支援向量機利用超平面將正類別和負類別區分開來（通常是在極高維度空間中）。

引數｜Parameter

機器學習系統自行訓練的模型的變數。

例如，權重就是一種引數，它們的值是機器學習系統通過連續的訓練迭代逐漸學習到的。引數的概念與超引數相對應。

測試集｜Test Set

資料集的子集，用於在模型經過驗證集驗證之後測試模型。當然，有時候我們不設定驗證集（主要用於模型調參），直接使用訓練資料訓練模型後就進行測試。

D

獨熱編碼｜One-Hot Encoding

一種稀疏向量，其中：

一個元素設為 1。
所有其他元素均設為 0。

One-Hot 編碼常用於表示擁有有限個可能值的字串或識別符號。例如，假設某個指定的植物學資料集記錄了 15000 個不同的物種，其中每個物種都用獨一無二的字串識別符號來表示。在特徵工程過程中，您可能需要將這些字串識別符號編碼為 One-Hot 向量，向量的大小為 15000。

獨立同分布

獨立就是每次抽樣之間是沒有關係的,不會相互影響。

同分布，意味著隨機變數 $X_1$ 和 $X_2$ 具有相同的分佈形狀和相同的分佈引數，對離散隨機變數具有相同的分佈律，對連續隨機變數具有相同的概率密度函式，有著相同的分佈函式，相同的期望、方差。

例如，某個網頁的訪問者在短時間內的分佈可能為獨立同分布，即分佈在該短時間內沒有變化，且一位使用者的訪問行為通常與另一位使用者的訪問行為無關。

迭代｜Iteration

模型的權重在訓練期間的一次更新，迭代包含計算引數在單個批量資料的梯度損失。

F

泛化｜Generalization

指的是模型依據訓練時採用的資料，針對以前未見過的新資料做出正確預測的能力。

反向傳播演算法｜Backpropagation

在神經網路上執行梯度下降法的主要演算法。該演算法會先按前向傳播方式計算（並快取）每個節點的輸出值，然後再按反向傳播遍歷圖的方式計算損失函式值相對於每個引數的偏導數。

G

過擬合｜Overfitting

建立的模型與訓練資料過於匹配，以致於模型無法根據新資料做出正確的預測。

如圖，綠線代表過擬合模型，黑線代表正則化模型。雖然綠線完美的匹配訓練資料，但太過依賴，並且與黑線相比，對於新的測試資料上具有更高的錯誤率。

H

混淆矩陣｜Confusion Matrix

一種 NxN 表格，用於總結分類模型的預測成效；即標籤和模型預測的分類之間的關聯。在混淆矩陣中，一個軸表示模型預測的標籤，另一個軸表示實際標籤。N 表示類別個數。在二元分類問題中，N=2。例如，下面顯示了一個二元分類問題的混淆矩陣示例：

腫瘤（預測的標籤）	非腫瘤（預測的標籤）
腫瘤（實際標籤）	18	1
非腫瘤（實際標籤）	6	452

上面的混淆矩陣顯示，在 19 個實際有腫瘤的樣本中，該模型正確地將 18 個歸類為有腫瘤（18 個真正例），錯誤地將 1 個歸類為沒有腫瘤（1 個假負例）。同樣，在 458 個實際沒有腫瘤的樣本中，模型歸類正確的有 452 個（452 個真負例），歸類錯誤的有 6 個（6 個假正例）。

多類別分類問題的混淆矩陣有助於確定出錯模式。例如，某個混淆矩陣可以揭示，某個經過訓練以識別手寫數字的模型往往會將 4 錯誤地預測為 9，將 7 錯誤地預測為 1。混淆矩陣包含計算各種效果指標（包括精確率和召回率）所需的充足資訊。

J

整合學習｜Ensemble

多個模型的預測結果的並集。

通俗來講，整合學習把大大小小的多種演算法融合在一起，共同協作來解決一個問題。整合學習可以用於分類問題整合，迴歸問題整合，特徵選取整合，異常點檢測整合等。

你可以通過以下一項或多項來建立整合學習：

不同的初始化
不同的超引數
不同的整體結構

決策邊界｜Decision Boundary

在二元分類或多類別分類問題中，模型學到的類別之間的分界線。例如，在以下表示某個二元分類問題的圖片中，決策邊界是橙色類別和藍色類別之間的分界線：

精確率｜Precision

一種分類模型指標。精確率指模型正確預測正類別的頻率。

$召回率 = \frac { 真正例數 } { 真正例數 + 假負例數 }$

交叉熵｜Cross-Entropy

對數損失函式向多類別分類問題進行的一種泛化。交叉熵可以量化兩種概率分佈之間的差異。

$H(p,q) = \sum_{i=1}^{n} p(x) \cdot log(\frac{1}{q(x)})$

啟用函式｜Activation Function

一種函式（例如 ReLU 或 S 型函式），用於對上一層的所有輸入求加權和，然後生成一個輸出值（通常為非線性值），並將其傳遞給下一層。

結構風險最小化｜Structural Risk Minimization

一種演算法，用於平衡以下兩個目標：

期望構建最具預測性的模型（例如損失最低）。
期望使模型儘可能簡單（例如強大的正則化）。

例如，旨在將基於訓練集的損失和正則化降至最低的模型函式就是一種結構風險最小化演算法。

L

離群點｜Outlier

與大多數其他值差別很大的值。在機器學習中，下列所有值都是離群值。

絕對值很高的權重。
與實際值相差很大的預測值。
值比平均值高大約 3 個標準偏差的輸入資料。

離群值常常會導致模型訓練出現問題。

類別｜Class

為標籤列舉的一組目標值中的一個。例如，在檢測垃圾郵件的二元分類模型中，兩種類別分別是「垃圾郵件」和「非垃圾郵件」。在識別狗品種的多類別分類模型中，類別可以是「貴賓犬」、「小獵犬」、「哈巴犬」等。

離散特徵｜Discrete Feature

一種特徵，包含有限個可能值。例如，某個值只能是「動物」、「蔬菜」或「礦物」的特徵便是一個離散特徵（或分類特徵）。與連續特徵相對。

M

密集層｜Dense Layer

是全連線層的同義詞。

P

批次｜Batch

模型訓練的一次迭代（即一次梯度更新）中使用樣本簇。

偏差｜Bias

距離原點的截距或偏移。偏差（也稱為偏差項）在機器學習模型中以 $b$ 或 $w_0$ 表示。例如，在下面的公式中，偏差為 $b$ ：

$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$

請勿與「預測偏差」混淆。

批次規模｜Batch Size

模型迭代一次，使用的樣本集的大小。

例如訓練集有 6400 個樣本，batch_size=128，那麼訓練完整個樣本集需要 50 次迭代。Batch Size 的大小一般設定為 16 及 16 的倍數。

R

ROC 曲線下面積

一種會考慮所有可能分類閥值的評價指標。

ROC 曲線下面積的數值意義為：對於隨機選擇的正類別樣本確實為正類別，以及隨機選擇的負類樣本為正類別，分類器更確信前者的概率。

S

輸入層｜Input Layer

神經網路中的第一層（接受輸入資料的層）

輸出層｜Output Layer

神經網路最後一層。

損失｜Loss

一種衡量指標，用於衡量模型的預測偏離其標籤的程度。或者更悲觀地說是衡量模型有多差。要確定此值，模型必須定義損失函式。例如，線性迴歸模型通常將均方誤差用於損失函式，而邏輯迴歸模型則使用對數損失函式。

收斂｜Convergence

通俗來說，收斂通常是指在訓練期間達到的一種狀態，即經過一定次數的迭代之後，訓練損失和驗證損失在每次迭代中的變化都非常小或根本沒有變化。也就是說，如果採用當前資料進行額外的訓練將無法改進模型，模型即達到收斂狀態。在深度學習中，損失值有時會在最終下降之前的多次迭代中保持不變或幾乎保持不變，暫時形成收斂的假象。

縮放｜Scaling

特徵工程中的一種常用做法，是對某個特徵的值區間進行調整，使之與資料集中其他特徵的值區間一致。例如，假設您希望資料集中所有浮點特徵的值都位於 0 到 1 區間內，如果某個特徵的值位於 0 到 500 區間內，您就可以通過將每個值除以 500 來縮放該特徵。

隨機梯度下降法｜SGD

SGD 依賴於從資料集中隨機均勻選擇的單個樣本來計算每步的梯度估算值。

Softmax 函式

一種函式，可提供多類別分類模型中每個可能類別的概率。這些概率的總和正好為 1.0。例如，softmax 可能會得出某個影象是狗、貓和馬的概率分別是 0.9、0.08 和 0.02。（也稱為完整 softmax。）

T

推斷｜Inference

在機器學習中，推斷通常指以下過程：通過將訓練過的模型應用於無標籤樣本來做出預測。在統計學中，推斷是指在某些觀測資料條件下擬合分佈引數的過程。

梯度｜Gradient

偏導數相對於所有自變數的向量。在機器學習中，梯度是模型函式偏導數的向量。

梯度下降法｜Gradient Descent

一種通過計算並且減小梯度將損失降至最低的技術，它以訓練資料為條件，來計算損失相對於模型引數的梯度。通俗來說，梯度下降法以迭代方式調整引數，逐漸找到權重和偏差的最佳組合，從而將損失降至最低。

特徵｜Feature

在進行預測時使用的輸入變數。

特徵組合｜Feature Cross

通過將單獨的特徵進行組合（相乘或求笛卡爾積）而形成的合成特徵。特徵組合有助於表示非線性關係。

特徵工程｜Feature Engineering

指以下過程：確定哪些特徵可能在訓練模型方面非常有用，然後將日誌檔案及其他來源的原始資料轉換為所需的特徵。

凸函式｜Convex Function

一種函式，函式影象以上的區域為凸集。典型凸函式的形狀類似於字母 U。例如，以下都是凸函式：

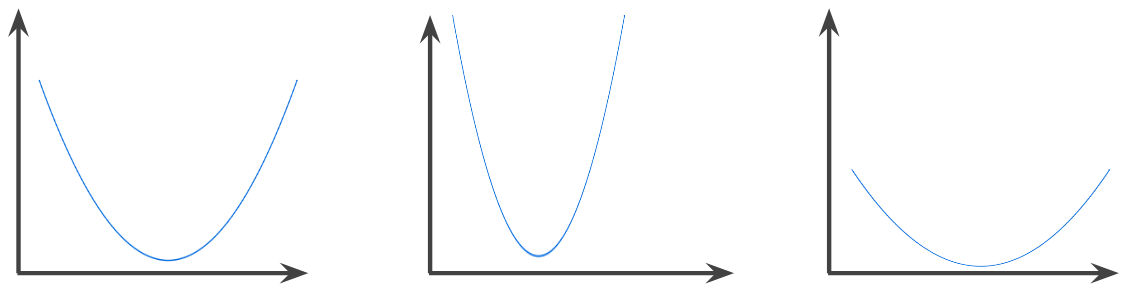
嚴格凸函式只有一個區域性最低點，該點也是全域性最低點。經典的 U 形函式都是嚴格凸函式。不過，有些凸函式（例如直線）則不是這樣。

很多常見的損失函式（包括下列函式）都是凸函式：

L2 損失函式
對數損失函式
L1 正則化
L2 正則化

梯度下降法的很多變體都一定能找到一個接近嚴格凸函式最小值的點。同樣，隨機梯度下降法的很多變體都有很高的可能效能夠找到接近嚴格凸函式最小值的點（但並非一定能找到）。

兩個凸函式的和（例如 L2 損失函式 + L1 正則化）也是凸函式。

深度模型絕不會是凸函式。值得注意的是，專門針對凸優化設計的演算法往往總能在深度網路上找到非常好的解決方案，雖然這些解決方案並不一定對應於全域性最小值。

凸優化｜Convex Optimization

使用數學方法（例如梯度下降法）尋找凸函式最小值的過程。機器學習方面的大量研究都是專注於如何通過公式將各種問題表示成凸優化問題，以及如何更高效地解決這些問題。

X

學習率｜Learning Rate

在訓練模型時用於梯度下降的一個變數。在每次迭代期間，梯度下降法都會將學習速率與梯度相乘。得出的乘積稱為梯度步長。

學習速率是一個重要的超引數。

稀疏特徵｜Sparse Feature

一種特徵向量，其中的大多數值都為 0 或為空。例如，某個向量包含一個為 1 的值和一百萬個為 0 的值，則該向量就屬於稀疏向量。再舉一個例子，搜尋查詢中的單詞也可能屬於稀疏特徵 - 在某種指定語言中有很多可能的單詞，但在某個指定的查詢中僅包含其中幾個。

與密集特徵相對。

協同過濾｜Collabroative Filtering

根據很多其他使用者的興趣來預測某位使用者的興趣。協同過濾通常用在推薦系統中。

Y

預訓練模型

已經過訓練的模型或模型元件（例如巢狀）。有時，您需要將預訓練的巢狀饋送到神經網路。在其他時候，您的模型將自行訓練巢狀，而不依賴於預訓練的巢狀。

Z

準確率｜Accuracy

分類模型的正確預測所佔的比例。在多類別分類中，準確率的定義如下：

$準確率 = \frac { 正確預測數 } { 樣本總數 }$

在二元分類中，準確率的定義如下：

$準確率 = \frac { 真正例數 + 真負例數 } { 樣本總數 }$

真負例

被模型正確地預測為負類別的樣本。例如，模型推斷出某封電子郵件不是垃圾郵件，而該電子郵件確實不是垃圾郵件。

真正例

被模型正確地預測為正類別的樣本。例如，模型推斷出某封電子郵件是垃圾郵件，而該電子郵件確實是垃圾郵件。

召回率

一種分類模型指標，用於回答以下問題：在所有可能的正類別標籤中，模型正確地識別出了多少個？即：

$召回率 = \frac { 真正例數 } { 真正例數 + 假正例數}$

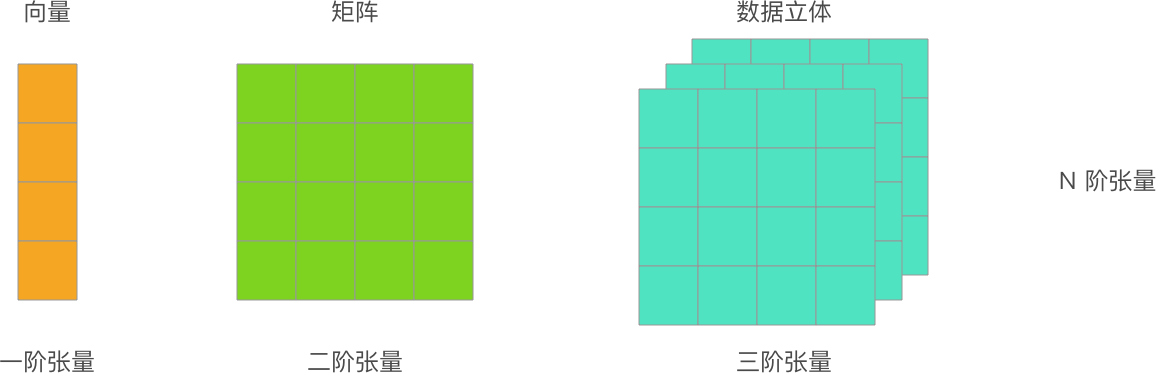
張量｜Tensor

TensorFlow 程式中的主要資料結構。張量是 N 維（其中 N 可能非常大）資料結構，最常見的是標量、向量或矩陣。張量的元素可以包含整數值、浮點值或字串值。

遷移學習｜Transfer Learning

將資訊從一個機器學習任務轉移到另一個機器學習任務。例如，在多工學習中，一個模型可以完成多項任務，例如針對不同任務具有不同輸出節點的深度模型。遷移學習可能涉及將知識從較簡單任務的解決方案轉移到較複雜的任務，或者將知識從資料較多的任務轉移到資料較少的任務。

大多數機器學習系統都只能完成一項任務。遷移學習是邁向人工智慧的一小步；在人工智慧中，單個程式可以完成多項任務。

L1 正則化｜L1 Regularization

一種正則化，根據權重的絕對值的總和來懲罰權重。在依賴稀疏特徵的模型中，L1 正則化有助於使不相關或幾乎不相關的特徵的權重正好為 0，從而將這些特徵從模型中移除。與 L2 正則化相對。

L2 正則化｜L2 Regularization

一種正則化，根據權重的平方和來懲罰權重。L2 正則化有助於使離群值（具有較大正值或較小負值）權重接近於 0，但又不正好為 0。（與 L1 正則化相對。）線上性模型中，L2 正則化始終可以改進泛化。

週期｜Epoch

在訓練時，整個資料集的一次完整遍歷，以便不漏掉任何一個樣本。因此，一個週期表示（N/批次規模）次訓練迭代，其中 N 是樣本總數。