Java 資料結構和演算法 - 排序
Java 資料結構和演算法 - 排序
本文討論陣列元素的排序問題,資料量不大,可以在記憶體中完成。
實現了Comparable介面的物件才可以排序。
插入排序和其他簡單排序
Insertion sort是一個簡單的排序演算法,適用於資料量少的情況。
/**
* Simple insertion sort
*/
public static <AnyType extends 插入排序的過程如下圖
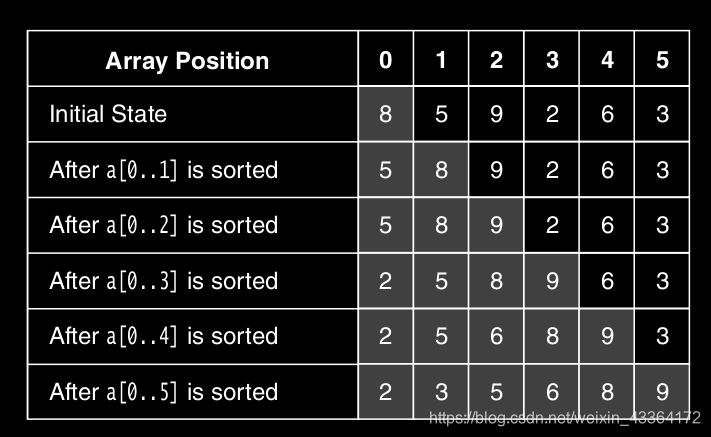
可以看到,演算法的複雜度是O(N2)。
希爾排序
第一個提升插入排序效能的是Shellsort。雖然它不是已知的最快演算法,但它是次二次(subquadratic)演算法,程式碼比插入排序稍長,是最簡單的快速演算法。
Shell的想法是避免大量資料移動,首先比較離的遠的元素,然後比較稍微近一些的元素,逐漸退回到基本的插入排序。Shellsort使用一個序列h1、h2、…、ht,叫做增量序列。只要h1 = 1,任何增量序列都會起作用,但有些選擇比其他選擇更好。一個階段完成以後,使用一些增量hk,當i+hk是有效的索引的時候,對每個i,我們有a[i] ≤ a[i+hk
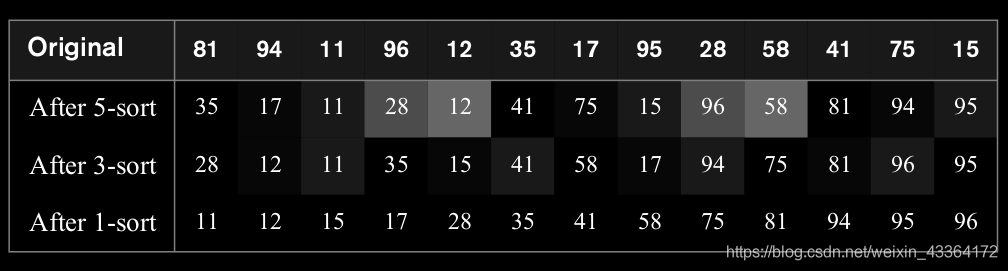
比如,上圖就是使用Shellsort幾個階段之後的陣列。在5-sort之後,間隔為5的元素已經排好序了。
類似地,在3-sort之後,間隔為3的元素已經排好序了。Shellsort的一個重要特性(還沒有被證明)是一個hk-sorted的陣列經過hk-1-sorted排序之後,仍然是hk-sorted。
一般來說,一個hk-sort需要,對hk、hk+1、…、N-1的每個位置i,把元素放到i、i-hk、i-2hk等等正確的位置。雖然這個順序不影響實現,還是要仔細檢查hk-sort在hk個獨立的子序列上執行插入排序(見上圖)。
看下面的程式碼,內迴圈代表一個gap insertion sort。在間隙插入排序內,在迴圈被執行後,陣列中由間隙分隔的元素被排好序。如果gap是1,就和插入排序一樣了。這樣,Shellsort也叫縮小差距排序。
/**
* Shellsort, using a sequence suggested by Gonnet.
*
* @param a an array of Comparable items.
*/
public static <AnyType extends Comparable<? super AnyType>> void shellsort(AnyType[] a) {
for (int gap = a.length / 2; gap > 0;
gap = gap == 2 ? 1 : (int) (gap / 2.2))
for (int i = gap; i < a.length; i++) {
AnyType tmp = a[i];
int j = i;
for (; j >= gap && tmp.compareTo(a[j - gap]) < 0; j -= gap)
a[j] = a[j - gap];
a[j] = tmp;
}
}
我們已經看到,當gap是1的時候,內迴圈就把陣列排好序了。如果gap不是1,總有一些元素還沒排好。
Shell建議gap從N/2開始,每次減半,直到1,問題就解決了。從下圖可以看到,不同的增量,排序效能是不一樣的。
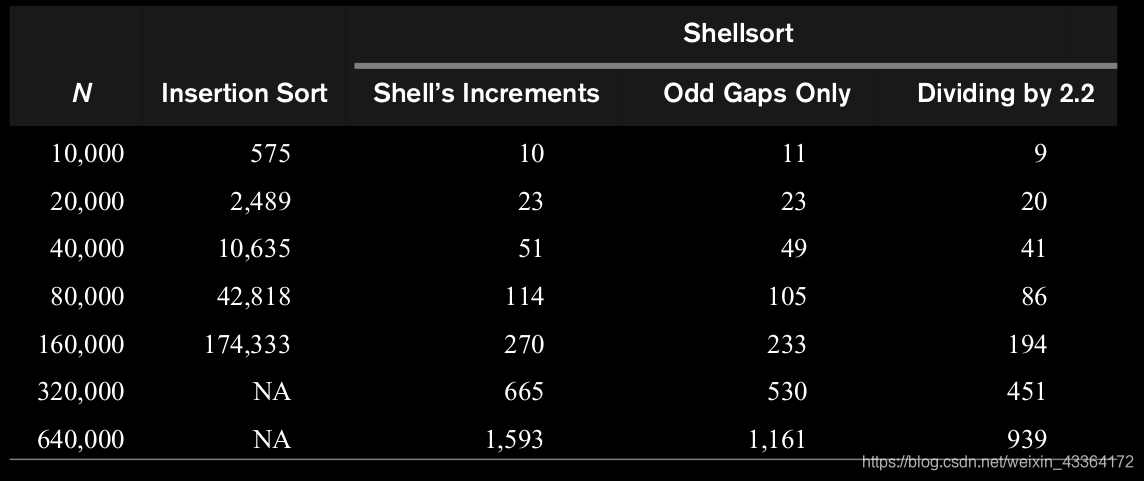
歸併排序
Mergesort採用分治演算法,遞迴地排序。
基本的歸併演算法接受兩個輸入陣列A和B,輸出一個數組C。有三個計數器Actr、Bctr和Cctr,初始設定為各自陣列的開頭。A[Actr]和B[Bctr]之中比較小的那個被拷貝到C的下一個元素,相應的計數器加1。當一個數組空了,另一個數組的剩餘元素被拷貝到C。
我們看一個例子:
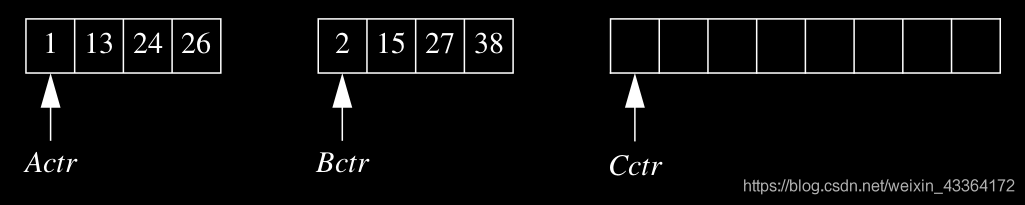
如果陣列A包含1、13、24、26,B包含2、15、27、38,演算法專業執行。首先,比較1和2,1被插入C,然後比較13和2:
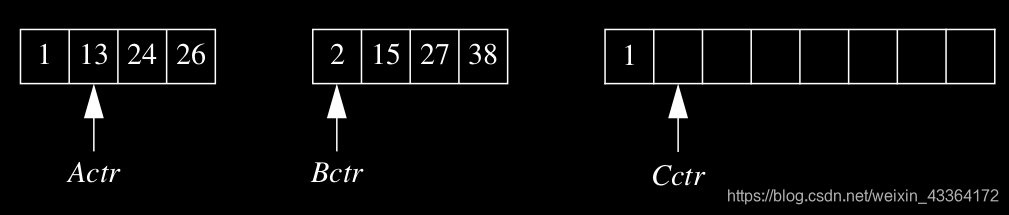
2被加到C,比較13和15

13被加到C,比較24和15

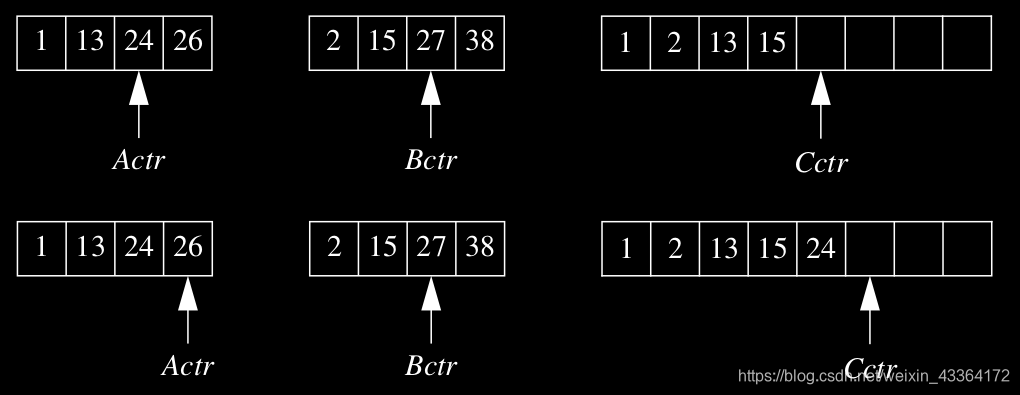
當26被加到C,A陣列空了

最後,B被拷貝到C

實現程式碼如下
/**
* Internal method that makes recursive calls.
*
* @param a an array of Comparable items.
* @param tmpArray an array to place the merged result.
* @param left the left-most index of the subarray.
* @param right the right-most index of the subarray.
*/
private static <AnyType extends Comparable<? super AnyType>> void mergeSort(AnyType[] a, AnyType[] tmpArray, int left, int right) {
if (left < right) {
int center = (left + right) / 2;
mergeSort(a, tmpArray, left, center);
mergeSort(a, tmpArray, center + 1, right);
merge(a, tmpArray, left, center + 1, right);
}
}
/**
* Internal method that merges two sorted halves of a subarray.
*
* @param a an array of Comparable items.
* @param tmpArray an array to place the merged result.
* @param leftPos the left-most index of the subarray.
* @param rightPos the index of the start of the second half.
* @param rightEnd the right-most index of the subarray.
*/
private static <AnyType extends Comparable<? super AnyType>> void merge(AnyType[] a, AnyType[] tmpArray, int leftPos, int rightPos, int rightEnd) {
int leftEnd = rightPos - 1;
int tmpPos = leftPos;
int numElements = rightEnd - leftPos + 1;
// Main loop
while (leftPos <= leftEnd && rightPos <= rightEnd)
if (a[leftPos].compareTo(a[rightPos]) <= 0)
tmpArray[tmpPos++] = a[leftPos++];
else
tmpArray[tmpPos++] = a[rightPos++];
while (leftPos <= leftEnd) // Copy rest of first half
tmpArray[tmpPos++] = a[leftPos++];
while (rightPos <= rightEnd) // Copy rest of right half
tmpArray[tmpPos++] = a[rightPos++];
// Copy tmpArray back
for (int i = 0; i < numElements; i++, rightEnd--)
a[rightEnd] = tmpArray[rightEnd];
}
/**
* Mergesort algorithm.
*
* @param a an array of Comparable items.
*/
public static <AnyType extends Comparable<? super AnyType>> void mergeSort(AnyType[] a) {
AnyType[] tmpArray = (AnyType[]) new Comparable[a.length];
mergeSort(a, tmpArray, 0, a.length - 1);
}
歸併排序在執行時嚴重依賴比較元素和移動元素的代價。Java的元素比較是昂貴的,因為比較操作由函式物件實現。而移動物件是廉價的,因為元素不用拷貝,而是簡單地修改引用。在所有的通用排序演算法中,歸併排序的比較操作比較少,所以是Java裡通用排序的好的候選。事實上,java.util.Arrays.sort對物件陣列排序時就使用了該演算法。而對於原始型別,java.util.Arrays.sort使用的是quicksort。
快速排序
quicksort是快速的分治演算法。它的平均執行時間是O(N log N)。它的速度主要歸功於緊湊而高度優化的內迴圈。一方面,快排演算法相對簡單容易懂,也已經被證明了,因為它依賴遞迴。另一方面,它是個棘手的演算法,程式碼的小改動,都可能造成執行時間的大波動。
考慮使用下面的簡單的排序演算法給列表排序:任意選擇一個元素,分成三組,小於它的、等於它的和大於它的。遞迴地個第一組和第三組排序,最後把三個組連線起來。程式碼見下,它的效能一般都不錯。事實上,如果列表含有大量的重複資料,只有幾個不同元素,效能會非常好。
public static void sort(List<Integer> items) {
if (items.size() > 1) {
List<Integer> smaller = new ArrayList<Integer>();
List<Integer> same = new ArrayList<Integer>();
List<Integer> larger = new ArrayList<Integer>();
Integer chosenItem = items.get(items.size() / 2);
for (Integer i : items) {
if (i < chosenItem)
smaller.add(i);
else if (i > chosenItem)
larger.add(i);
else
same.add(i);
}
sort(smaller); // Recursive call!
sort(larger); // Recursive call!
items.clear();
items.addAll(smaller);
items.addAll(same);
items.addAll(larger);
}
}
該演算法描述了快排的基本形式。對於其他列表,這樣遞迴,很難比歸併排序更快。為了做地更好,我們必須避免使用大量的額外記憶體和保持內迴圈的乾淨。這樣,快排一般避免增加第二個組(等於組),演算法有很多影響效能的微小細節。下面描述最常用的快排實現,輸入是一個數組,演算法不增加額外的陣列。
快排演算法Quicksort(S)可分為四步:
- 如果S的元素數量是0或者1,就返回
- 選擇S中的任一元素v,叫pivot
- 把S–{v}(S的剩餘元素)分成兩個不相交的組:L = {x∈S – {v} | x≤v}和R = {x∈S – {v} | x≥v}
- 返回Quicksort(L)的結果,然後是v,接著是Quicksort®
有幾點值得注意。首先,遞迴的S可能是空的。其次,任何元素都可以當pivot,但是不同的選擇,會影響效能。三,演算法允許等於pivot的其他元素放到L或者R。
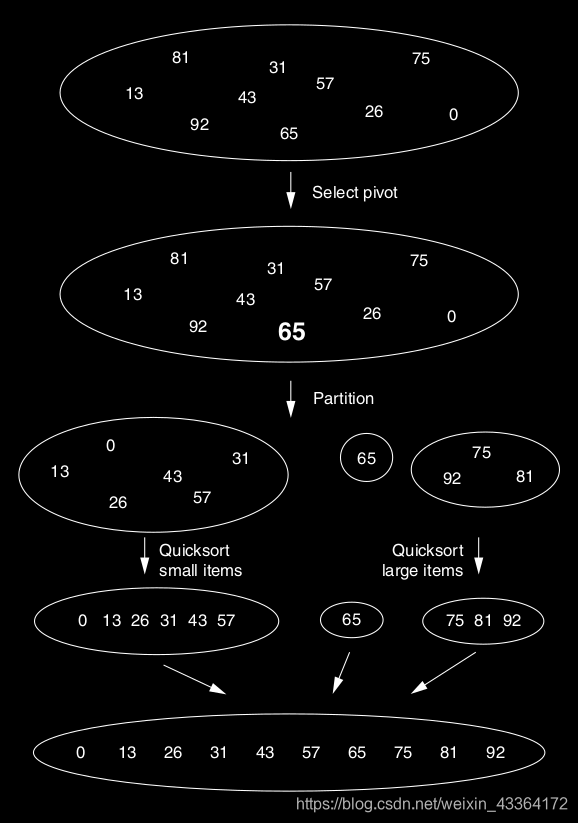
上面的圖,pivot是65。剩餘元素分成兩個子集。然後,每個組都遞迴地排序。Java的實現,元素被儲存在由小於的和大於的分隔的陣列的一部分中。分割槽之後,pivot在陣列的索引p處,後來的遞迴呼叫,會在小於p-1的部分和大於p+1的兩部分分別進行。
快排比歸併演算法快,是因為分割槽比歸併快。
選擇pivot
一般可以選擇中間元素,(low+high)/2。
median-of-three partitioning是個更好的辦法-選擇第一個、中間一個和最後一個的中位數。
分割槽策略
有幾種選擇策略,先討論最簡單的一種。可分為三步
- 交換pivot和最後一個元素
- 把小於pivot的放到左邊,大於的放到右邊-使用計數器i,從左往右搜比pivot大的元素,找到就停止;使用計數器j,從右往左搜比pivot小元素,找到就停止;如果i<j,就交換並繼續;否則停止
- 交換位置i的元素和pivot元素

程式碼是這樣的
/**
* Quicksort algorithm.
*
* @param a an array of Comparable items.
*/
public static <AnyType extends Comparable<? super AnyType>> void quicksort(AnyType[] a) {
quicksort(a, 0, a.length - 1);
}
private static final int CUTOFF = 10;
/**
* Method to swap to elements in an array.
*
* @param a an array of objects.
* @param index1 the index of the first object.
* @param index2 the index of the second object.
*/
public static final <AnyType> void swapReferences(AnyType[] a, int index1, int index2) {
AnyType tmp = a[index1];
a[index1] = a[index2];
a[index2] = tmp;
}
/**
* Internal quicksort method that makes recursive calls.
* Uses median-of-three partitioning and a cutoff of 10.
*
* @param a an array of Comparable items.
* @param low the left-most index of the subarray.
* @param high the right-most index of the subarray.
*/
private static <AnyType extends Comparable<? super AnyType>> void quicksort(AnyType[] a, int low, int high) {
if (low + CUTOFF > high)
insertionSort(a, low, high);
else {
// Sort low, middle, high
int middle = (low + high) / 2;
if (a[middle].compareTo(a[low]) < 0)
swapReferences(a, low, middle);
if (a[high].compareTo(a[low]) < 0)
swapReferences(a, low, high);
if (a[high].compareTo(a[middle]) < 0)
swapReferences(a, middle, high);
// Place pivot at position high - 1
swapReferences(a, middle, high - 1);
AnyType pivot = a[high - 1];
// Begin partitioning
int i, j;
for (i = low, j = high - 1; ; ) {
while (a[++i].compareTo(pivot) < 0)
;
while (pivot.compareTo(a[--j]) < 0)
;
if (i >= j)
break;
swapReferences(a, i, j);
}
// Restore pivot
swapReferences(a, i, high - 1);
quicksort(a, low, i - 1); // Sort small elements
quicksort(a, i + 1, high); // Sort large elements
}
}
/**
* Internal insertion sort routine for subarrays
* that is used by quicksort.
*
* @param a an array of Comparable items.
* @param low the left-most index of the subarray.
*/
private static <AnyType extends Comparable<? super AnyType>> void insertionSort(AnyType[] a, int low, int high) {
for (int p = low + 1; p <= high; p++) {
AnyType tmp = a[p];
int j;
for (j = p; j > low && tmp.compareTo(a[j - 1]) < 0; j--)
a[j] = a[j - 1];
a[j] = tmp;
}
}
快速選擇
和排序密切相關的問題是選擇,比如在含有N個元素的陣列中找到kth個最小元素。還有變種是找到中位數、或者N/2th個最小元素。修改一下快排演算法,可以解決選擇問題。
Quickselect(S, k)的步驟如下
- 如果S只有一個元素,想必k也是1,可以返回元素
- 在S中任意選擇元素v,它是pivot
- 把S–{v}分成L和R,就像快排中做過的
- 如果k小於或者等於L中的元素數量,搜尋的元素肯定在L中。遞迴呼叫Quickselect(L, k)。否則,如果k恰好比L中元素數量大1,則pivot就是最小kth元素,可以返回。否則,最小kth元素位於R,並且是R中的最小(k–|L|–1)th元素。然後,我們遞迴呼叫返回結果
Quickselect只有一個遞迴,而快排是兩個。quickselect的最壞情況與快排的情況相同,也是二次的(如果遞迴發生在空集上)。
/**
* Quick selection algorithm.
* Places the kth smallest item in a[k-1].
*
* @param a an array of Comparable items.
* @param k the desired rank (1 is minimum) in the entire array.
*/
public static <AnyType extends Comparable<? super AnyType>> void quickSelect(AnyType[] a, int k) {
quickSelect(a, 0, a.length - 1, k);
}
/**
* Internal selection method that makes recursive calls.
* Uses median-of-three partitioning and a cutoff of 10.
* Places the kth smallest item in a[k-1].
*
* @param a an array of Comparable items.
* @param low the left-most index of the subarray.
* @param high the right-most index of the subarray.
* @param k the desired rank (1 is minimum) in the entire array.
*/
private static <AnyType extends Comparable<? super AnyType>> void quickSelect(AnyType[] a, int low, int high, int k) {
if (low + CUTOFF > high)
insertionSort(a, low, high);
else {
// Sort low, middle, high
int middle = (low + high) / 2;
if (a[middle].compareTo(a[low]) < 0)
swapReferences(a, low, middle);
if (a[high].compareTo(a[low]) < 0)
swapReferences(a, low, high);
if (a[high].compareTo(a[middle]) < 0)
swapReferences(a, middle, high);
// Place pivot at position high - 1
swapReferences(a, middle, high - 1);
AnyType pivot = a[high - 1];
// Begin partitioning
int i, j;
for (i = low, j = high - 1; ; ) {
while (a[++i].compareTo(pivot) < 0)
;
while (pivot.compareTo(a[--j]) < 0)
;
if (i >= j)
break;
swapReferences(a, i, j);
}
// Restore pivot
swapReferences(a, i, high - 1);
// Recurse; only this part changes
if (k <= i)
quickSelect(a, low, i - 1, k);
else if (k > i + 1)
quickSelect(a, i + 1, high, k);
}
}
