映象（反射）矩陣是n維空間中的沿n-1維平面的一種矩陣變換，常見的應用場景是在2維空間影象處理、3維空間物體場景變換。先直觀看看映象變換的效果：

        直觀的感受了映象變換的效果之後，接下來我們看看這個變換的數學表示式是什麼樣的。首先n維度空間的映象變換是基於某個n-1維度平面（對於2維度就是某條直線）來說的，線性代數的知識知道n維空間的n-1維平面存在法向量，假設是要做映象平面的單位法向量，單位法向量||u||=1，定義映象矩陣。

        1. Q是對稱和標準正交的，

        由Q的矩陣展開形式，很明顯看到，所以Q是對稱的。標準正交：是Q的兩列，由標準正交的定義，需要滿足如下條件：

         2.,這條性質反應了映象的特點，映象兩次等於原空間。

        上面是映象矩陣的定義和它的一些性質和推導，那麼我們再做一點深層次的思考：為什麼映象的表達會是一個矩陣變換，如果我做旋轉是不是也是一個矩陣變換？首先，問題2的答案：YES,2維空間的旋轉的變換矩陣是：

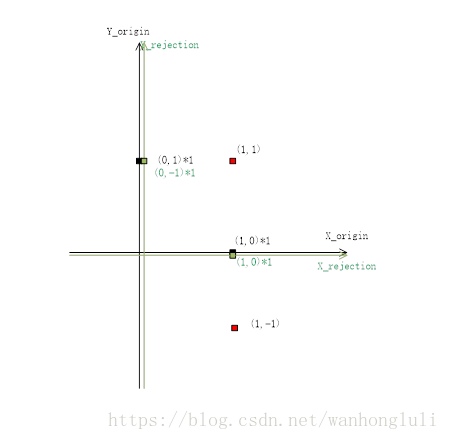
        對於問題1，矩陣變換的本質可以理解成座標系的變換，對於映象和旋轉我們都是對原座標系中的向量（座標系中的點可以表示成原點指向該點的向量）用新的座標系中的基進行了表示。比如二維直角座標系x0y的座標基向量是（1，0）和（0，1），如果用矩陣表示：,基向量就是矩陣的列向量，(1,1)點這個座標系下的座標（x,y）由方程組求得(x，y)=（1，1）因為在原座標系下，假設我們對（1，1）點做沿x軸做映象，這裡的映象很簡單，x軸和原座標系相同，y軸與原座標系反號，所以映象之後新的座標系基向量是(1,0)和(0,-1)（如果你通過上面的映象公式可以求得同樣的答案，u=(0,1)）,新的座標系的矩陣表示

        最後我們說說2維度空間和3維空間的映象矩陣的表示式，首先是2維空間，對於2-D空間的某個條直線做映象，假設該直線的單位法向量u（x，y），由計算得到2-D空間的映象矩陣：

        對於3-D空間的某平面做映象：