一般情況下，當$H_0: \beta_1 = 0$ 被接受的時候，表明 $y$ 的取值傾向不隨 $x$ 的值按線性關係變化。這種情況的原因可能是變數 $y$ 與 $x$ 之間的相關關係不顯著，也可能是 $y$ 與 $x$ 並非線性相關。 當$H_0: \beta_1 = 0$ 被拒絕的時候，如果沒有其它資訊，只能認為因變數 $y$ 對 $x$ 的線性迴歸是有效的，但並沒有說明迴歸的有效程度，不能斷言 $y$ 與 $x$ 之間一定是線性相關關係，而不是曲線關係或其他關係。這時候圖形表現就很重要了。

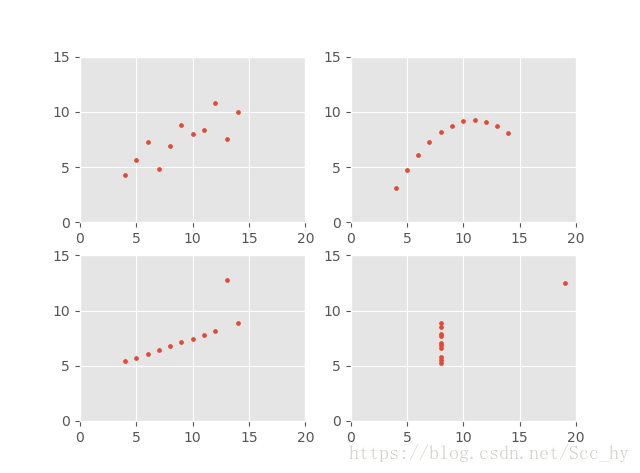
4組資料示例

1-資料準備

import numpy as np
x1 =
 
 list(range(4,15))
x4 = [8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 19]
y1 = [4.26, 5.68, 7.24, 4.82, 6.95, 8.81, 8.04, 8.33, 10.84, 7.58, 9.96]
y2 = [3.10, 4.74, 6.13, 7.26, 8.14, 8.77, 9.14, 9.26, 9.13, 8.74, 8.10]
y3 = [5.39, 5.73, 6.08, 6.44, 6.77, 7.11, 7.46, 7.81, 8.15, 12.74, 8.84]
y4 = [6.58, 5.76, 7.71, 8.84
 
, 8.47, 7.04, 5.25, 5.56, 7.91, 6.89, 12.5]
x1_in = np.array(x1).reshape(-1,1)
x4_in = np.array(x4).reshape(-1,1)
y1_in = np.array(y1).reshape(-1,1)
y2_in = np.array(y2).reshape(-1,1)
y3_in = np.array(y3).reshape(-1,1)
y4_in = np.array(y4).reshape(-1,1)

圖示

import matplotlib.pyplot as plt
plt.style.
 
use('ggplot')
plt.subplot(2,2,1)
plt.xlim(0,20),plt.ylim(0,15)
plt.scatter(x1_in, y1_in,s = 8)
plt.subplot(2,2,2)
plt.xlim(0,20),plt.ylim(0,15)
plt.scatter(x1_in, y2_in, s = 8)
plt.subplot(2,2,3)
plt.xlim(0,20),plt.ylim(0,15)
plt.scatter(x1_in, y3_in,s = 8)
plt.subplot(2,2,4)
plt.xlim(0,20),plt.ylim(0,15)
plt.scatter(x4_in, y4_in,s = 8)
plt.show()

2-迴歸

from sklearn.linear_model import LinearRegression 
lrg1 = LinearRegression()
lrg1.fit(x1_in,y1_in)
lrg2 = LinearRegression()
lrg2.fit(x1_in,y2_in)
lrg3 = LinearRegression()
lrg3.fit(x1_in,y3_in)
lrg4 = LinearRegression()
lrg4.fit(x4_in,y4_in)
get_lr_stats(x1_in, y1_in, lrg1)
get_lr_stats(x1_in, y2_in, lrg2)
get_lr_stats(x1_in, y3_in, lrg3)
get_lr_stats(x4_in, y4_in, lrg4)

四個模型引數幾乎一樣( get_lr_stats 在Python_一元線性迴歸及迴歸顯著性 中) 但是並非全都是線性迴歸

>>> get_lr_stats(x1_in, y1_in, lrg1)
一元線性迴歸方程為:     y=3.000090909090906 + 0.5000909090909094*x
相關係數(R^2)： 0.6665424595087752；
迴歸分析(SSR)： 27.51000090909094；     殘差(SSE)： 13.76269；
           F ： 17.989942967676996；    pf ： 0.002169628873078789
           t ： 4.689105252775333；     pt ： 0.0005687504416628528
>>> get_lr_stats(x1_in, y2_in, lrg2)
一元線性迴歸方程為:     y=3.0009090909090883 + 0.5000000000000002*x
相關係數(R^2)： 0.6662420337274844；
迴歸分析(SSR)： 27.500000000000014；    殘差(SSE)： 13.776290909090912；
           F ： 17.965648492271313；    pf ： 0.002178816236910796
           t ： 4.685937987627148；     pt ： 0.0005712964612135407
>>> get_lr_stats(x1_in, y3_in, lrg3)
一元線性迴歸方程為:     y=3.007545454545453 + 0.49936363636363645*x
相關係數(R^2)： 0.6660467267232798；
迴歸分析(SSR)： 27.430044545454564；    殘差(SSE)： 13.753319090909097；
           F ： 17.949878082322083；    pf ： 0.0021848056073100444
           t ： 4.683880856554066；     pt ： 0.0005729566449371534
>>> get_lr_stats(x4_in, y4_in, lrg4)
一元線性迴歸方程為:     y=3.0017272727272726 + 0.4999090909090909*x
相關係數(R^2)： 0.6667072568984653；
迴歸分析(SSR)： 27.490000909090913；    殘差(SSE)： 13.742490000000004；
           F ： 18.003288209183207；    pf ： 0.0021646023471972213
           t ： 4.690844158819928；     pt ： 0.0005673577949779548

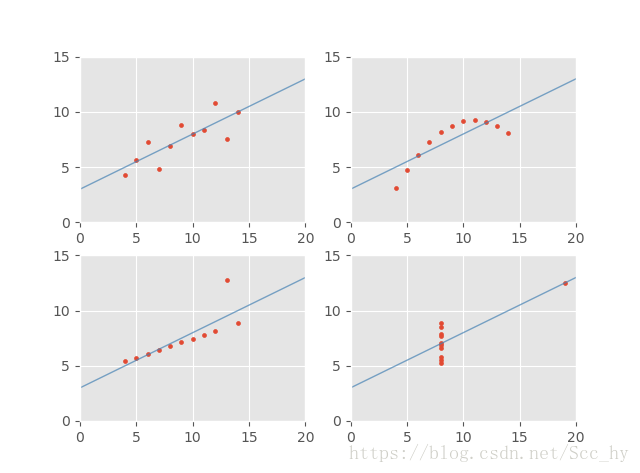
3-迴歸圖示

## 迴歸後圖示
xl = np.array(list(range(0,21))).reshape(-1,1)
plt.subplot(2,2,1)
plt.xlim(0,20),plt.ylim(0,15)
plt.scatter(x1_in, y1_in,s = 8)
plt.plot(xl, lrg1.predict(xl),c='steelblue', alpha=0.7, lw=1)

plt.subplot(2,2,2)
plt.xlim(0,20),plt.ylim(0,15)
plt.scatter(x1_in, y2_in, s = 8)
plt.plot(xl, lrg1.predict(xl),c='steelblue', alpha=0.7, lw=1)

plt.subplot(2,2,3)
plt.xlim(0,20),plt.ylim(0,15)
plt.scatter(x1_in, y3_in,s = 8)
plt.plot(xl, lrg1.predict(xl),c='steelblue', alpha=0.7, lw=1)

plt.subplot(2,2,4)
plt.xlim(0,20),plt.ylim(0,15)
plt.scatter(x4_in, y4_in,s = 8)
plt.plot(xl, lrg1.predict(xl),c='steelblue', alpha=0.7, lw=1)
plt.show()

因此，在實際應用中，不應該侷限於一種方法去分析判斷。要得到，確實可信的結果，應該將F檢驗、散點圖、殘差分析等方法一起使用，得到一致的結果才可以下定論