這裡我們用到了特徵篩，為什麼要進行特徵進行選擇？ 在一個數據集中，我們需要找出對因變數影響顯著的變數，對於顯著性較低的我們進行剔除，留下顯著性高的特徵把它們加入模型，從而使我們的模型複雜度更低，更加的簡潔，準確。

這篇文章使用反向淘汰的方法來進行此項工作

反向淘汰步驟：

• 確定我們用來衡量顯著性的一個閾值（決定取捨），這裡我們取0.05
• 將所有的特徵ALL IN到模型進行訓練
• 計算出每個特徵的P_value
• 將P_value最高的且高於顯著水平的閾值的特徵從模型訓練中剔除
• 利用剩下的特徵進行新一輪的擬合，如果存在P_value大於閾值，則返回4步，直到所有特徵的P_value小於設定的閾值

關於P_value： - p值是指在一個概率模型中，統計摘要（如兩組樣本均值差）與實際觀測資料相同，或甚至更大這一事件發生的概率。換言之，是檢驗假設零假設成立或表現更嚴重的可能性。p值若與選定顯著性水平（0.05或0.01）相比更小，則零假設會被否定而不可接受。然而這並不直接表明原假設正確。p值是一個服從正態分佈的隨機變數，在實際使用中因樣本等各種因素存在不確定性。產生的結果可能會帶來爭議。 - 零假設（null hypothesis），統計學術語，又稱原假設，指進行統計檢驗時預先建立的假設。 零假設成立時，有關統計量應服從已知的某種概率分佈。 當統計量的計算值落入否定域時，可知發生了小概率事件，應否定原假設。

資料集說明：

CRIM：城鎮人均犯罪率。 ZN：住宅用地超過 25000 sq.ft. 的比例。 INDUS：城鎮非零售商用土地的比例。 CHAS：查理斯河空變數（如果邊界是河流，則為1；否則為0）。 NOX：一氧化氮濃度。 RM：住宅平均房間數。 AGE：1940 年之前建成的自用房屋比例。 DIS：到波士頓五個中心區域的加權距離。 RAD：輻射性公路的接近指數。 TAX：每 10000 美元的全值財產稅率。 PTRATIO：城鎮師生比例。 B：1000（Bk-0.63）^ 2，其中 Bk 指代城鎮中黑人的比例。 LSTAT：人口中地位低下者的比例。 MEDV：自住房的平均房價，以千美元計。

#匯入用到的庫
import sklearn.datasets as datasets
import pandas as pd
import numpy as np
#載入資料集
Boston = datasets.load_boston()
# print(Boston.feature_names)
x = Boston.data   #shape:(506, 13)
y = Boston.target   #shape:(506,)

由於多元線性迴歸基本方程為： 因此需要在變數矩陣新增一列全一：（該操作也是反向淘汰的準備工作）

#資料預處理
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
x = ss.fit_transform(x)#特徵縮放

x = np.append(arr=np.ones((x.shape[0],1)),values= x ,axis = 1) #新增方程式常數項的係數
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.25,random_state = 0)#分割資料集為訓練集與測試集

#建立迴歸器並擬合數據
import statsmodels.formula.api as sm
x_option = x_train[:,[0,1,2,3,4,5,6,7,8,9,10,11,12,13]]
ols = sm.OLS(endog= y_train,exog=x_option,).fit()
ols.summary()   #查看回歸器的引數資訊

輸出： 可以看到x_3（特徵I–NDUS。）的P_value是最高的且高於設定的閾值，將之剔除

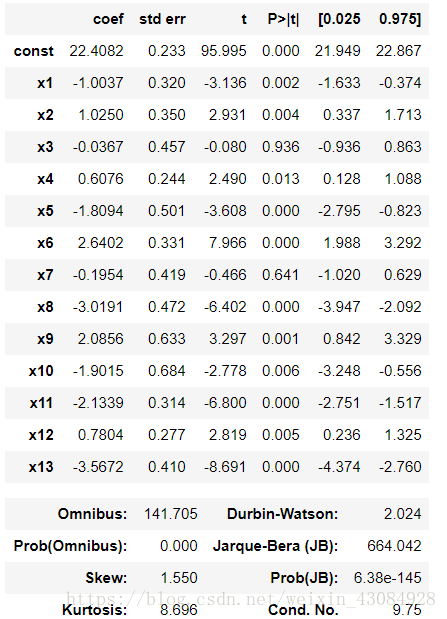
新一輪擬合：

x_option = x_train[:,[0,1,2,4,5,6,7,8,9,10,11,12,13]]
ols = sm.OLS(endog= y_train,exog=x_option,).fit()
ols.summary() 

輸出： 這次也是剔除x_6不過這裡的x_3對應的是X_train的第7個變數（加了一列）即（RM：住宅平均房間數） 迴圈處理，知道所留下的特徵的P_value都低於顯著水平閾值 最後：

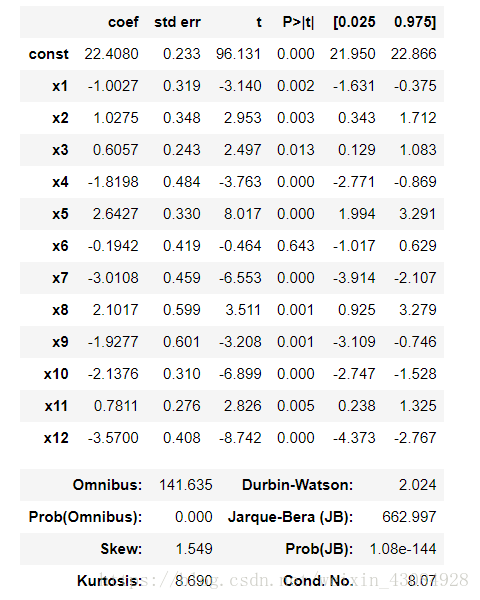
X_opt = X_train[:,[0,1,2,4,5,6,8,9,10,11,12,13]]
regressor_OLS = sm.OLS(endog=Y_train,exog=X_opt).fit()
regressor_OLS.summary() 

輸出： 可以看到剩下的P_value小於設定的顯著水平，這就是最終的結果了。

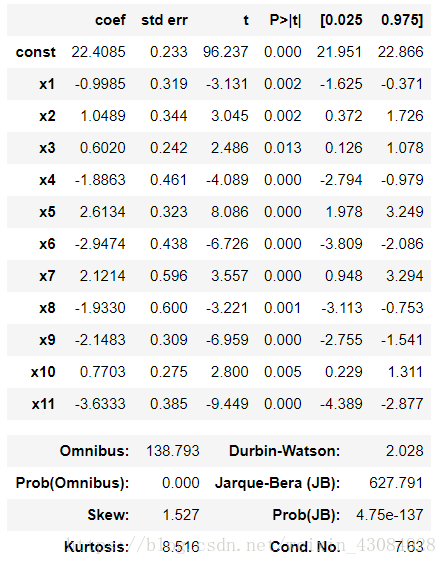
#利用擬合好的最終模型，進行測試集的預測
y_pre = ols.predict(x_test[:,[0,1,2,4,5,6,8,9,10,11,12,13]])

#模型評估
from sklearn.metrics import r2_score, mean_squared_error 
print(r2_score(y_test,y_pre))#（確定係數）迴歸分數函式。
print(mean_squared_error(y_test,y_pre))  #均方誤差迴歸損失

輸出：

r2_score : 0.6368341501259818
mean_squared_error : 29.670292375423013
#結論看，模型不怎麼好。。哈哈哈

接下來嘗試用多次項試試看下結果：

#資料的載入與處理
Boston = datasets.load_boston()
x = Boston.data   #shape:(506, 13)
y = Boston.target   #shape:(506,)

from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
x = ss.fit_transform(x)  #特徵縮放

x = x[:,[0,1,2,4,5,6,8,9,10,11,12]]  #這裡採用了上文剔除特徵的結果
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.25,random_state = 0)#分割資料集

from sklearn.preprocessing import PolynomialFeatures
pf = PolynomialFeatures(degree=2)
x_train = pf.fit_transform(x_train)#這個操作會自動增加常數項的係數，用法可以參考文件

#建立模型
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor = regressor.fit(x_train,y_train)

#預測測試集
x_test = pf.fit_transform(x_test)  #對測試集也進行多項處理
y_pre = regressor.predict(x_test) #預測

#模型評估
from sklearn.metrics import r2_score, mean_squared_error 
print(r2_score(y_test,y_pre))   #（確定係數）迴歸分數函式。
print(mean_squared_error(y_test,y_pre))  #均方誤差迴歸損失

輸出：

r2_score : 0.7530871120604362
mean_squared_error : 20.17253984362321

貌似稍微好了一些。也不知道做對了沒，或者大家有什麼好的方案，歡迎交流~