題目描述

Mayan Puzzle是最近流行起來的一個遊戲。遊戲介面是一個7行×5列的棋盤，上面堆放著一些方塊，方塊不能懸空堆放，即方塊必須放在最下面一行，或者放在其他方塊之上。遊戲通關是指在規定的步數內消除所有的方塊，消除方塊的規則如下：

1 、每步移動可以且僅可以沿橫向（即向左或向右）拖動某一方塊一格：當拖動這一方塊時，如果拖動後到達的位置（以下稱目標位置）也有方塊，那麼這兩個方塊將交換位置（參見輸入輸出樣例說明中的圖6到圖7）；如果目標位置上沒有方塊，那麼被拖動的方塊將從原來的豎列中抽出，並從目標位置上掉落（直到不懸空，參見下面圖1和圖2）；

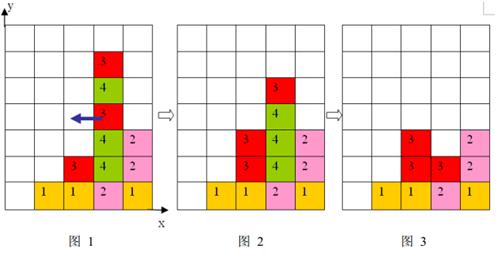
2 、任一時刻，如果在一橫行或者豎列上有連續三個或者三個以上相同顏色的方塊，則它們將立即被消除（參見圖1到圖3）。

注意：

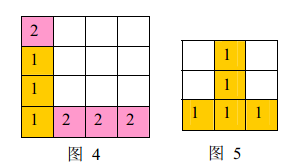
a) 如果同時有多組方塊滿足消除條件，幾組方塊會同時被消除（例如下面圖4，三個顏色為1 的方塊和三個顏色為 2 的方塊會同時被消除，最後剩下一個顏色為2的方塊）。

b) 當出現行和列都滿足消除條件且行列共享某個方塊時，行和列上滿足消除條件的所有方塊會被同時消除（例如下面圖5所示的情形，5個方塊會同時被消除）。

3 、方塊消除之後，消除位置之上的方塊將掉落，掉落後可能會引起新的方塊消除。注意：掉落的過程中將不會有方塊的消除。

上面圖1到圖3給出了在棋盤上移動一塊方塊之後棋盤的變化。棋盤的左下角方塊的座標為（0, 0），將位於（3, 3）的方塊向左移動之後，遊戲介面從圖1變成圖2所示的狀態，此時在一豎列上有連續三塊顏色為4的方塊，滿足消除條件，消除連續3塊顏色為4的方塊後，上方的顏色為3的方塊掉落，形成圖3所示的局面。

輸入輸出格式

輸入格式：

共 6 行。

第一行為一個正整數n，表示要求遊戲通關的步數。

接下來的5行，描述7×5 的遊戲介面。每行若干個整數，每兩個整數之間用一個空格隔開，每行以一個0結束，自下向上表示每豎列方塊的顏色編號（顏色不多於10種，從1開始順序編號，相同數字表示相同顏色）。

輸入資料保證初始棋盤中沒有可以消除的方塊。

輸出格式：

如果有解決方案，輸出n行，每行包含3個整數x,y,g，表示一次移動，每兩個整數之間用一個空格隔開，其中(x ,y)表示要移動的方塊的座標，g 表示移動的方向，1 表示向右移動，−1表示向左移動。注意：多組解時，按照x為第一關健字，y為第二關健字，1優先於−1 ，給出一組字典序最小的解。遊戲介面左下角的座標為(0 ,0)。

如果沒有解決方案，輸出一行，包含一個整數−1。

輸入輸出樣例

輸入樣例#1： 複製

3
1 0
2 1 0
2 3 4 0
3 1 0
2 4 3 4 0

輸出樣例#1： 複製

2 1 1
3 1 1
3 0 1

說明

【輸入輸出樣例說明】

按箭頭方向的順序分別為圖6到圖11

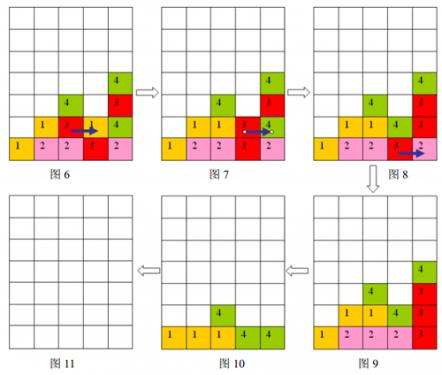
樣例輸入的遊戲局面如上面第一個圖片所示，依次移動的三步是：(2 ,1)處的方格向右移動，(3,1)處的方格向右移動，(3,0)處的方格向右移動，最後可以將棋盤上所有方塊消除。

【資料範圍】

對於30%的資料，初始棋盤上的方塊都在棋盤的最下面一行；

對於100%的資料，0<n≤5 。

NOIP2011提高組day1第3題

題解：

首先觀察範圍和初步分析可確定本題應用搜索演算法，因為題目中步數小於5，範圍很小，因而考慮用DFS而非BFS。而還要保證步驟字典序最小，因此選擇從左到右，從下到上的搜尋順序，同時發現，方塊左移和方塊右移可以在特殊記錄空方塊右移（在輸出答案時特殊考慮一下）後統一考慮為方塊右移，因而搜尋順序為：從左到右，從上到下，只考慮方塊右移。

然後就可以開始搜尋了，不過本題還有一些比較棘手的步驟，即方塊的下落和消除，以及小細節：搜尋的優化。

考慮方塊下落。我們可以把同一列的方塊先收集到一個佇列中，清空該列，然後在將佇列中的元素彈出，順次放在棋盤的該列即可。這樣下落問題就解決了。再考慮方塊的消除，暴力的消除會比較麻煩，因此想到用一個標記陣列來輔助消除。每次以一個位置為起點，搜尋橫三和縱三的方塊，在標記陣列中打標記，就可以解決在消除中方塊公用的問題了。

最後是搜尋的優化：

第一、我們已經從搜尋順序上進行了優化，找到的第一個解就是字典序最小的解；

第二、如果一個狀態中某一種方塊的個數大於0而小於三，則該方塊永遠不會被消除，可以判定當前狀態失敗，直接返回上一層；

第三、在考慮方塊的移動時，只需考慮顏色不同的方塊的交換。

到此，所有的步驟就都清楚了，總結一下，本題需要的不僅僅是搜尋，還有在處理模擬過程中的一些技巧，還有搜尋的剪枝，是不可多得的好題。

程式碼如下。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<queue>
using namespace std;
const int maxn=10;
int n;
int state[maxn][maxn];
struct Answer{
	int x,y;
	bool flag;//flag=true表示方塊向左移動,如此定義達到剪枝目的.
}ans[maxn];
bool Empty(){//判斷棋盤是否為空.
	for (int i=0;i<5;i++)
		for (int j=0;j<7;j++)
			if (state[i][j]) return false;
	return true;
}
void Drop(){//方塊下落.
	queue <int> Q;
	for (int i=0;i<5;i++){
		int cnt=0;
		for (int j=0;j<7;j++)
			if (state[i][j]) Q.push(state[i][j]);//先把所有方塊收集到一個佇列裡.
		memset(state[i],0,sizeof(state[i]));//清空該列.
		while (!Q.empty()) state[i][cnt++]=Q.front(),Q.pop();//將佇列中的元素彈出放到棋盤中.
	}
}
bool Clear(){
	bool CanClear;//能否消除標記.
	bool mark[maxn][maxn];
	memset(mark,false,sizeof(mark));
	for (int i=0;i<5;i++){
		for (int j=0;j<7;j++){
			if (state[i][j]==0) continue;//沒有方塊.
			int tempx;
			for (tempx=i;tempx+1<5 && state[tempx+1][j]==state[i][j];tempx++);
			//用tempx找到橫向能消除的最右位置.
			if (tempx-i>=2){//如果(橫向)相連的方塊長度超過3,則能消除.
				for (int tx=i;tx<=tempx;tx++) mark[tx][j]=true;//在mark陣列對應的位置上打上標記.
				CanClear=true;//能消除.
			}
			int tempy;
			for (tempy=j;tempy+1<7 && state[i][tempy+1]==state[i][j];tempy++);
			//用tempy找到縱向能找到的最上位置.
			if (tempy-j>=2){//如果(縱向)相連的方塊長度超過3,則能消除.
				for (int ty=j;ty<=tempy;ty++) mark[i][ty]=true;//在mark陣列對應的位置上打上標記.
				CanClear=true;//能消除.
			}
		}
	}
	for (int i=0;i<5;i++)
		for (int j=0;j<7;j++)
			if (mark[i][j]) state[i][j]=0;//將打上標記的方塊全部消除.
	return CanClear;//返回是否能消除.
}
void DFS(int depth){
	if (depth>n){//運算元用盡.
		if (Empty()){//如果為空則輸出操作序列.
			for (int i=1;i<=n;i++)
				if (ans[i].flag) printf("%d %d %d\n",ans[i].x+1,ans[i].y,-1);
				else printf("%d %d %d\n",ans[i].x,ans[i].y,1);
			exit(0);//直接結束程式.
		}
		return ;
	}
	int sum[maxn*2]={0};
	//統計每個顏色的方塊的數量.
	for (int i=0;i<5;i++)
		for (int j=0;j<7;j++) sum[state[i][j]]++;
	//剪枝--如果某方塊的數量小於三,則該種方塊一定不可以被消除,失敗.
	for (int i=1;i<=15;i++)
		if (sum[i]!=0 && sum[i]<3) return ;
	for (int i=0;i<4;i++)//這種搜尋順序能夠保證搜到的第一種方案就是字典序最小的.
		for (int j=0;j<7;j++){
			if (state[i][j]==state[i+1][j]) continue;//剪枝--如果顏色相同,則無需交換.
			ans[depth].x=i,ans[depth].y=j,ans[depth].flag=(!state[i][j]);//記錄當前操作.
			int temp[maxn][maxn];
			memcpy(temp,state,sizeof(temp));//將當前狀態存到臨時陣列中,防止丟失.
			swap(state[i][j],state[i+1][j]);//進行操作(交換).
			Drop();//先掉落.
			while (Clear()) Drop();//反覆消除、掉落.
			DFS(depth+1);//迭代搜尋.
			ans[depth].x=0,ans[depth].y=0,ans[depth].flag=0;//清空當前操作.
			memcpy(state,temp,sizeof(state));//還原當前狀態.
		}
}
int main(){
//	freopen("Mayan.in","r",stdin);
//	freopen("Mayan.out","w",stdout);
	scanf("%d",&n);
	for (int i=0;i<5;i++)
		for (int j=0;;j++){
			scanf("%d",&state[i][j]);
			if (state[i][j]==0) break;
		}
	DFS(1);
	printf("-1\n");//無解情況.
	return 0;
}