對梯度下降法和反向傳播BP的一點理解
最近在學習深度學習中的梯度下降與反向傳播方面的知識。偶有心得,特此記錄。若有不足之處,煩請指正賜教。
在訓練階段,深度神經網路經過前向傳播之後,得到的預測值與先前給出真實值之間存在差距。我們可以使用損失函式來體現這種差距。損失函式的作用可以理解為:當前向傳播得到的預測值與真實值接近是,取較小值。反之取值增大。並且,損失函式應是以(w, b)為自變數的函式。
這裡就需要理解,所謂的對於神經網路的訓練指的是什麼。通過輸入大量訓練資料,使得神經網路中的各引數調整到一個合理的值。那麼我們在測試時,測試資料就可以直接與這些引數進行運算,準確地得到我們想要的輸出。
因此,重點在於,怎樣通過大量的訓練資料,使得引數自動調整到合理值。
普遍使用的是梯度下降法。它基於這樣的一種認識,通過某一群引數的運算後,若得到的預測值與真實值的差距(即損失函式取值)較小,則可以認為這一群引數是“較為令人滿意的”。於是明顯的,能夠使損失函式取其最小值的引數必然是我們想要的引數。
由淺入深,我們最容易想到的實現上述目的的方法是窮舉。即取遍引數的所有可能取值,比較在不同取值情況下得到的損失函式的值,即可得到使損失函式取值最小時的引數值。然而這種方法顯然是不可取的。因為在深度神經網路中,引數的數量是一個可怕的數字,動輒上萬,十幾萬。並且,其取值有時是十分靈活的,甚至精確到小數點後若干位。若使用窮舉法,將會造成一個幾乎不可能實現的計算量。
第二個想到的方法就是微分。通過將損失函式進行全微分,取微分為零或較小的點,即可得到理想引數。(補充:損失函式取下凸函式,才能使得此方法可行。現實中選取的各種損失函式大多也正是如此。)可面對神經網路中龐大的引數總量,純數學方法幾乎是不可能直接得到微分零點的。
因此我們使用了梯度下降法。既然無法直接獲得該點,那麼我們就想要一步一步逼近該點。一個常見的形象理解是,爬山時一步一步朝著坡度最陡的山坡往下,即可到達山谷最底部。(至於為何不能閃現到谷底,原因是引數數量龐大,表示式複雜,無法直接計算)我們都知道,向量場的梯度指向的方向是其函式值上升最快的方向,也即其反方向是下降最快的方向。計算梯度的方式就是求偏導。
這裡需要引入一個步長的概念。個人理解是:此梯度對引數當前一輪學習的影響程度。步長越大,若以平面直角座標系中的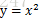
梯度這個概念對於理解神經網路中引數具體是怎樣更新的有很大幫助。
同樣,由簡到繁。我們首先想到的使用梯度下降法的具體做法是:損失函式對每一個引數自變數求偏導。然後每個偏導數乘以預先設定的步長,一次為本次學習的引數調整量。原引數減去引數調整量,則本輪學習結束。(注:學習不止一輪)
做法大體上確實如此(針對於批量梯度下降法)。我之前在理解梯度下降法時一直有一個錯誤的認識,即“損失函式是以預測值為自變數的函式”(其實是以引數為自變數)。這個誤解使我在面對梯度一詞時顯得格外迷茫。因為求偏導數必定與自變數有關,而我一直誤將引數調整侷限於輸出層。其實是對網路中所有引數求梯度。
具體的實現方法,使用的是反向傳播。
反向傳播有核心的四條公式。我在此談談自己的一點理解。我認為前兩條公式就像是多米諾骨牌一樣(求導的鏈式法則)。第一條公式求出輸出層每個神經元的誤差(推到第一枚多米諾骨牌),第二條公式闡述了後面一層網路神經元的誤差與前一層神經元的梯度的誤差(前一枚倒下可推匯出下一枚也倒下)。而第三四條公式,只是說明怎樣以神經元誤差得到兩個引數(w, b)的梯度。
注:上述“誤差”與“梯度”個人感覺並無太大差別。因為梯度乘以步長就是誤差。之所以分別用兩個詞(誤差用於神經元,梯度用於引數),是為了使讀者有意識地去區別神經元與引數。
引數是我們需要得到的,需要訓練調整的,結合梯度下降法這一名詞,在第三第四條公式中我使用了“梯度”去描述它。而隱藏層神經元(輸入輸出層神經元例外)的取值是一箇中間值,它由引數所確定,並不是我們的最終目標產物。同樣的,核心公式出現的δ符號指的都是神經元取值上的誤差。理解了這一點,看公式時思路就順暢很多。
理解神經元取值與引數是兩個概念後,我們再來看看四條公式。
- 輸出層誤差可如是計算。數學原理不難。
- 淺層網路的神經元取值誤差可由深層網路神經元取值誤差得到(需求和,即一個淺層網路神經元需由多個深層神經元共同反推得出),利用求導的鏈式法則。由此,整個網路的神經元取值誤差可以得出。
- 計算權重w的梯度:上一層(向淺)神經元取值 * 本層神經元誤差
- 計算偏置b的梯度:等於本層神經元誤差
至於何謂本層,應該是引數與經由其產生的神經元視為一層吧。(不確定)
公式中有些細節,即啟用函式。在深度神經網路中,在經過引數運算生成心的一層神經網路後,還要使用啟用函式進行運算。而啟用函式在反向傳播中也是很重要的一部分。留心何謂啟用函式,能使你更好地理解反向傳播的公式。

