梯度下降法和誤差反向傳播推導
阿新 • • 發佈:2019-01-25
梯度下降法原理
梯度下降法的示意圖如下
前提:假設
現有,
上式可以將
上式形成了一個誤差曲面,即
為了求得
當然,當
其中
神經網路的誤差反向傳播
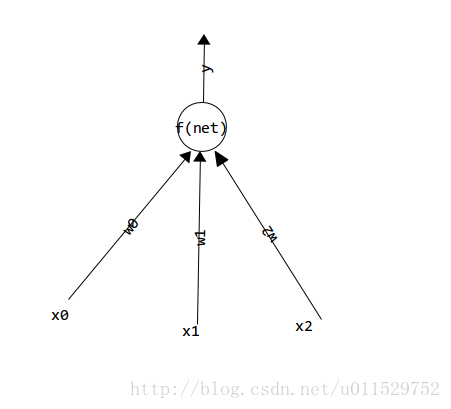
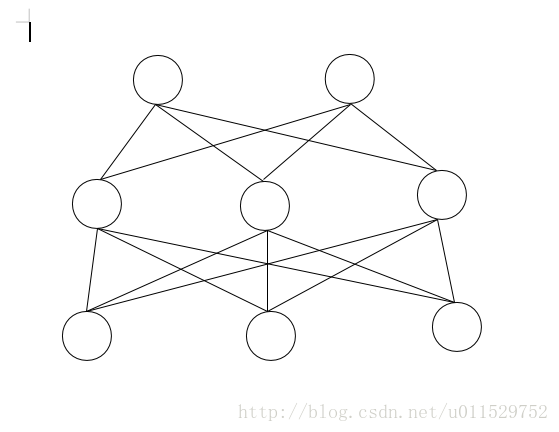
上面兩圖是簡單的神經元和神經網路模型
模型假設:
現在假設神經元有三層
從上到下的座標為
梯度下降法的示意圖如下
前提:假設
現有,


上面兩圖是簡單的神經元和神經網路模型
模型假設:
現在假設神經元有三層
從上到下的座標為