機器學習資料、特徵處理、模型融合
一 解決問題流程:
o 瞭解場景和目標
o 瞭解評估準則
o 認識資料
o 資料預處理(清洗,調權)
o 特徵工程
o 模型調參
o 模型狀態分析
o 模型融合
二 資料預處理
(1) 資料清洗
a: 不可信的樣本丟掉
b: 預設值極多的欄位考慮不用
(2) 資料取樣
a:下/上取樣
b:保證樣本均衡
三 特徵工程
1 特徵處理
(1) 數值型
(2) 類別型
(3)時間類
(4)文字型
(5)統計型
(6)組合特徵
(1) 數值型
a: 幅度調整/歸一化 幅度調整到[0,1]範圍內
b: 統計值max, min, mean, std
c: 離散化
d: Hash分桶
e: 每個類別下對應的變數統計值histogram(分佈狀況)
f: 試試 數值型 => 類別型
(2) 類別型:處理方式如下
a: one-hot編碼/ 啞變數 pd.get_dummies()
b: Hash與聚類處理
c: 小技巧:統計每個類別變數下各個target比例,轉成數值型
(3)時間類:處理方式如下
既可以看做連續值,也可以看做離散值
連續值
a) 持續時間(單頁瀏覽時長)
b) 間隔時間(上次購買/點選離現在的時間)
離散值
a) 一天中哪個時間段(hour_0-23)
b) 一週中星期幾(week_monday...)
c) 一年中哪個星期
d) 一年中哪個季度
e) 工作日/週末
(4)文字型
a: 詞袋
文字資料預處理後,去掉停用詞,剩下的片語成的list,在詞庫中的對映稀疏向量。
b: 使用Tf–idf 特徵
TF-IDF是一種統計方法,用以評估一字詞對於一個檔案集或一個語料庫中的其中一份檔案的重要程度。字詞的重要性隨著它在檔案中出現的次數成正比增加,但同時會隨著它在語料庫中出現的頻率成 反比下降。
(5)統計型
a: 加減平均:商品價格高於平均價格多少,使用者在某個品類下消費超過平均使用者多少,使用者連續登入天數超過平均多少...
b: 分位線:商品屬於售出商品價格的多少分位線處
c: 次序型:排在第幾位
d: 比例類:電商中,好/中/差評比例,你已超過全國百分之…的同學
(6)組合特徵
a: 簡單組合特徵:拼接型
user_id&&category: 10001&&女裙 10002&&男士牛仔
user_id&&style: 10001&&蕾絲 10002&&全棉
b: 模型特徵組合
用GBDT產出特徵組合路徑
組合特徵和原始特徵一起放進LR訓練
最早Facebook使用的方式,多家網際網路公司在用
2 特徵選擇
(1)原因:
冗餘:部分特徵的相關度太高了,消耗計算效能。
噪聲:部分特徵是對預測結果有負影響
(2)特徵選擇 VS 降維
前者只踢掉原本特徵裡和結果預測關係不大的,後者做特徵的計算組合構成新特徵.
SVD或者PCA確實也能解決一定的高維度問題
(3)常見特徵選擇方式
過濾型、包裹型、嵌入型
a: 過濾型
評估單個特徵和結果值之間的相關程度,排序留下Top相關的特徵部分。
Pearson相關係數,互資訊,距離相關度
缺點:沒有考慮到特徵之間的關聯作用,可能把有用的關聯特徵誤踢掉。
b:包裹型
把特徵選擇看做一個特徵子集搜尋問題,篩選各種特徵子集,用模型評估效果。
典型的包裹型演算法為 “遞迴特徵刪除演算法”(recursive feature elimination algorithm)
比如用邏輯迴歸,怎麼做這個事情呢?
① 用全量特徵跑一個模型
② 根據線性模型的係數(體現相關性),刪掉5-10%的弱特徵,觀察準確率/auc的變化
③ 逐步進行,直至準確率/auc出現大的下滑停止
c:嵌入型
根據模型來分析特徵的重要性(有別於上面的方式,是從生產的模型權重等)。
最常見的方式為用正則化方式來做特徵選擇。
舉個例子,最早在電商用LR做CTR預估,在3-5億維的係數特徵上用L1正則化的LR模型。剩餘2-3千萬的feature,意味著其它的feature重要度不夠。
模型融合方法:
1 Voting
模型融合其實也沒有想象的那麼高大上,從最簡單的Voting說起,這也可以說是一種模型融合。假設對於一個二分類問題,有3個基礎模型,那麼就採取投票制的方法,投票多者確定為最終的分類。
2 Averaging
對於迴歸問題,一個簡單直接的思路是取平均。稍稍改進的方法是進行加權平均。權值可以用排序的方法確定,舉個例子,比如A、B、C三種基本模型,模型效果進行排名,假設排名分別是1,2,3,那麼給這三個模型賦予的權值分別是3/6、2/6、1/6
這兩種方法看似簡單,其實後面的高階演算法也可以說是基於此而產生的,Bagging或者Boosting都是一種把許多弱分類器這樣融合成強分類器的思想。
3 Bagging
Bagging就是採用有放回的方式進行抽樣,用抽樣的樣本建立子模型,對子模型進行訓練,這個過程重複多次,最後進行融合。大概分為這樣兩步:
- 重複K次
- 有放回地重複抽樣建模
- 訓練子模型
2.模型融合
- 分類問題:voting
- 迴歸問題:average
Bagging演算法不用我們自己實現,隨機森林就是基於Bagging演算法的一個典型例子,採用的基分類器是決策樹。R和python都整合好了,直接呼叫。
4 Boosting
Bagging演算法可以並行處理,而Boosting的思想是一種迭代的方法,每一次訓練的時候都更加關心分類錯誤的樣例,給這些分類錯誤的樣例增加更大的權重,下一次迭代的目標就是能夠更容易辨別出上一輪分類錯誤的樣例。最終將這些弱分類器進行加權相加。引用加州大學歐文分校Alex Ihler教授的兩頁PPT
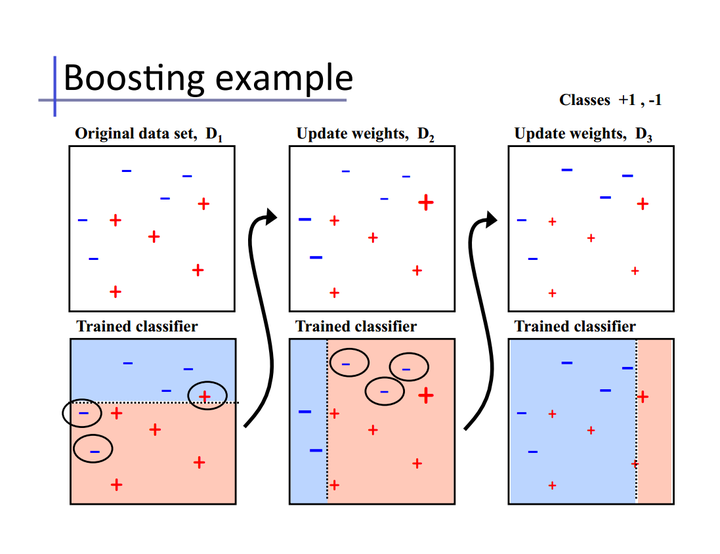
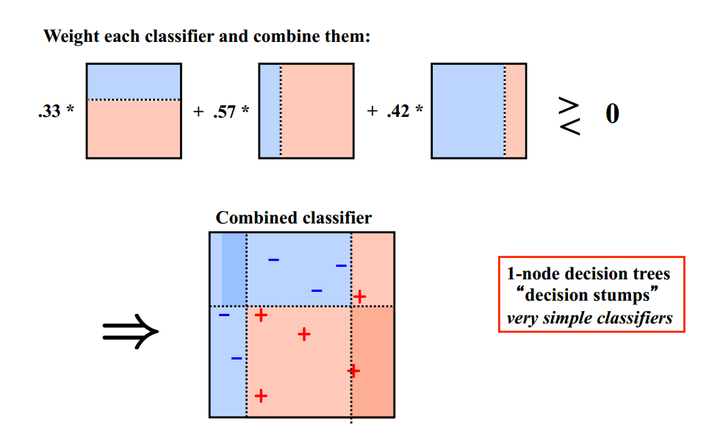
同樣地,基於Boosting思想的有AdaBoost、GBDT等,在R和python也都是整合好了直接呼叫。
PS:理解了這兩點,面試的時候關於Bagging、Boosting的區別就可以說上來一些,問Randomfroest和AdaBoost的區別也可以從這方面入手回答。也算是留一個小問題,隨機森林、Adaboost、GBDT、XGBoost的區別是什麼?
5 Stacking
Stacking方法其實弄懂之後應該是比Boosting要簡單的,畢竟小几十行程式碼可以寫出一個Stacking演算法。我先從一種“錯誤”但是容易懂的Stacking方法講起。
Stacking模型本質上是一種分層的結構,這裡簡單起見,只分析二級Stacking.假設我們有3個基模型M1、M2、M3。
1. 基模型M1,對訓練集train訓練,然後用於預測train和test的標籤列,分別是P1,T1
對於M2和M3,重複相同的工作,這樣也得到P2,T2,P3,T3。
2. 分別把P1,P2,P3以及T1,T2,T3合併,得到一個新的訓練集和測試集train2,test2.
3. 再用第二層的模型M4訓練train2,預測test2,得到最終的標籤列。
Stacking本質上就是這麼直接的思路,但是這樣肯定是不行的,問題在於P1的得到是有問題的,用整個訓練集訓練的模型反過來去預測訓練集的標籤,毫無疑問過擬合是非常非常嚴重的,因此現在的問題變成了如何在解決過擬合的前提下得到P1、P2、P3,這就變成了熟悉的節奏——K折交叉驗證。我們以2折交叉驗證得到P1為例,假設訓練集為4行3列
將其劃分為2部分
用traina訓練模型M1,然後在trainb上進行預測得到preb3和pred4
在trainb上訓練模型M1,然後在traina上進行預測得到pred1和pred2
然後把兩個預測集進行拼接
對於測試集T1的得到,有兩種方法。注意到剛剛是2折交叉驗證,M1相當於訓練了2次,所以一種方法是每一次訓練M1,可以直接對整個test進行預測,這樣2折交叉驗證後測試集相當於預測了2次,然後對這兩列求平均得到T1。
或者直接對測試集只用M1預測一次直接得到T1。
P1、T1得到之後,P2、T2、P3、T3也就是同樣的方法。理解了2折交叉驗證,對於K折的情況也就理解也就非常順利了。所以最終的程式碼是兩層迴圈,第一層迴圈控制基模型的數目,每一個基模型要這樣去得到P1,T1,第二層迴圈控制的是交叉驗證的次數K,對每一個基模型,會訓練K次最後拼接得到P1,取平均得到T1。這下再把@Wille博文中的那張圖片放出來就很容易看懂了。
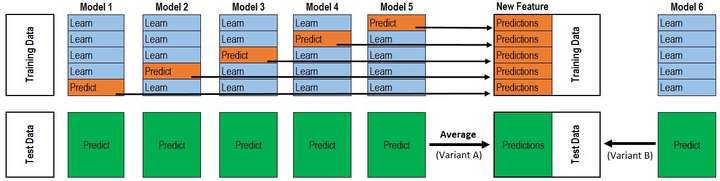
該圖是一個基模型得到P1和T1的過程,採用的是5折交叉驗證,所以迴圈了5次,拼接得到P1,測試集預測了5次,取平均得到T1。而這僅僅只是第二層輸入的一列/一個特徵,並不是整個訓練集。再分析作者的程式碼也就很清楚了。也就是剛剛提到的兩層迴圈。
以上是理論上的講解,下面通過一個例子來講解
本文以Kaggle的Titanic(泰坦尼克預測)入門比賽來講解stacking的應用(兩層!)。
資料的行數:train.csv有890行,也就是890個人,test.csv有418行(418個人)。
而資料的列數就看你保留了多少個feature了(通過特徵工程預處理),因人而異。這裡train保留了 7+1(1是預測列)。
在網上為數不多的stacking內容裡,相信你早看過了這張圖:
因為這張圖極具‘誤導性’。
把圖改了一下:
別找不同了,就是最上面 Model2,3,4,5 改成了 Model1,1,1,1
對於每一輪的 5-fold,Model 1都要做滿5次的訓練和預測。
Titanic 栗子:
Train Data有890行。(請對應圖中的上層部分)
每1次的fold,都會生成 713行 小train, 178行 小test。我們用Model 1來訓練 713行的小train,然後預測 178行 小test。預測的結果是長度為 178 的預測值。
這樣的動作走5次! 長度為178 的預測值 X 5 = 890 預測值,剛好和Train data長度吻合。這個890預測值是Model 1產生的,我們先存著,因為,一會讓它將是第二層模型的訓練來源。
重點:這一步產生的預測值我們可以轉成 890 X 1 (890 行,1列),記作 P1 (大寫P)
接著說 Test Data 有 418 行。(請對應圖中的下層部分,對對對,綠綠的那些框框)
每1次的fold,713行 小train訓練出來的Model 1要去預測我們全部的Test Data(全部!因為Test Data沒有加入5-fold,所以每次都是全部!)。此時,Model 1的預測結果是長度為418的預測值。
這樣的動作走5次!我們可以得到一個 5 X 418 的預測值矩陣。然後我們根據行來就平均值,最後得到一個 1 X 418 的平均預測值。
重點:這一步產生的預測值我們可以轉成 418 X 1 (418行,1列),記作 p1 (小寫p)
藍綠色是同步進行的:
走到這裡,你的第一層的Model 1完成了它的使命。
第一層還會有其他Model的,比如 Model 2,同樣的走一遍, 我們有可以得到 890 X 1 (P2) 和 418 X 1 (p2) 列預測值。
這樣吧,假設你第一層有3個模型,這樣你就會得到:
來自5-fold的預測值矩陣 890 X 3,(P1,P2, P3) 和 來自Test Data預測值矩陣 418 X 3, (p1, p2, p3)。
到第二層了………………
來自5-fold的預測值矩陣 890 X 3 作為你的Train Data,訓練第二層的模型
來自Test Data預測值矩陣 418 X 3 就是你的Test Data,用訓練好的模型來預測他們吧。
stack方法Python實現
具體例子可參考這篇部落格:部落格
from sklearn.model_selection import KFold
# Some useful parameters which will come in handy later on
ntrain = train.shape[0]
ntest = test.shape[0]
SEED = 0 # for reproducibility
NFOLDS = 5 # set folds for out-of-fold prediction
kf = KFold(n_splits=NFOLDS, random_state=SEED, shuffle=False)
def get_oof(clf, x_train, y_train, x_test):
oof_train = np.zeros((ntrain,))
oof_test = np.zeros((ntest,))
oof_test_skf = np.empty((NFOLDS, ntest)) #NFOLDS行,ntest列的二維array
for i, (train_index, test_index) in enumerate(kf.split(x_train)): #迴圈NFOLDS次
x_tr = x_train[train_index]
y_tr = y_train[train_index]
x_te = x_train[test_index]
clf.fit(x_tr, y_tr)
oof_train[test_index] = clf.predict(x_te)
oof_test_skf[i, :] = clf.predict(x_test) #固定行填充,迴圈一次,填充一行
oof_test[:] = oof_test_skf.mean(axis=0) #axis=0,按列求平均,最後保留一行
return oof_train.reshape(-1, 1), oof_test.reshape(-1, 1) #轉置,從一行變為一列參考文獻:



