第一部分：學習內容概要

• 程式開發過程
• 問題求解
• 演算法和演算法分析
• 資料結構

第二部分：學習筆記

• 程式開發過程

  框架圖

分析，嚴格化——設計——編碼——檢查，翻譯——測試/除錯

  牛頓迭代法      0.對給定正實數x和允許誤差e，令變數y取任意正實數值，如：y = x;   1.如果y*y與x足夠接近，即 | y * y - x | < e，計算結束並把y作為結果；   2.取z =（y + x / y）/ 2；   3.將z作為y的新值，回到步驟1.

（舉個栗子：完成平方根計算的Python函式）

    def sqrt(x):
    		y = 1.0
    		while abs( y * y - x ) > 1e-6
    			y = ( y +x / y) / 2
    			return y
 

• 問題求解   交叉路口的紅綠燈安排   貪婪演算法（貪心法）：根據當時掌握的資訊，儘可能地向得到解的方向前進，知道不能急需再換一個方向。這樣做通常找不到最優解，但能找到可以接受的解。   紅綠燈問題求解過程： 1.有關工作開始於交叉路口的抽象圖示，首先美劇出所有允許通行方向； 2.根據通行方向和有關不同方向衝突的定義，畫出衝突圖； 3.把通行方向的分組問題歸結為衝突圖中不相鄰頂點的劃分問題，用求出不相鄰頂點的分組作為交叉路口中可以同時通行的方向的分組。

  （具體實現）

  def coloring(G):
  	color = 0
  	groups = set()
  	verts = vertices(G)
  	while verts:
  		new_group = set()
  		for v in list(verts):
  		if not_adjacent_with_set(v, newgroup, G):
  			new_group.add(v)
  			verts.remove(v)
  		groups.add((color, new_group))
  		color += 1
  	return groups
   
  

• 演算法和演算法分析

  • 三個基本概念

    問題：一個問題W是需要解決（需要用計算求解）的一個具體需求。（例如判斷人一個正整數N是否為素數）

    問題例項：問題W的一個例項w是該問題的一個具體例子，通常可以通過一組具體的引數設定。（例如判斷1013是否為素數）

    演算法：解決問題W的一個演算法A，是對一種計算過程的嚴格描述。對W的任何一個例項w，實施演算法A描述的計算過程，就能得到w的解。（例如一個判斷素數的演算法應該能給出1013是否為素數的判斷，也能滿足其他正整數是否為素數的判斷）

  • 演算法的性質

      1.有窮性：一個演算法的描述應該由有限多條指令或語言構成。

      2.能行性：演算法中的指令的含義嚴格而且明確，所描述的操作過程可以完全機械的進行。

      3.確定性：作用於所求解問題的給定輸入（以某種描述形式給出的要處理問題的具體例項），根據演算法的描述將產生出唯一的確定的一個動作序列。

      4.終止性（行為的有窮性）：對問題的任何例項，演算法產生的動作序列都是有窮的，他或者終止並給出該問題例項的解；或者終止並指出給定的輸入無解。

      5.輸入/輸出：有確定定義的輸入和輸出。

  • 演算法和程式

      演算法的實現：程式可以看作採用計算裝置能夠處理的語言描述的演算法，由於它是演算法的實際體現，又能在實際計算機上執行，因此被稱為演算法的實現

  • 演算法設計與分析   1.列舉法：根據具體問題枚舉出各種可能，從中選出有用資訊或者問題的解。

      2.貪心法：見上文

      3.分治法：把複雜問題分解為相對簡單的子問題，分別求解，最後通過組合去子問題的接的方式得到原問題的解。

      4.回溯法（搜尋法）：專指通過探索的方式求解。分步驟進行，進行不下去了推翻原先的步驟，另行選擇求解路徑。

      5.動態規劃法：在一些複雜情況下，問題求解很難直截了當地進行，因此需要在前面的步驟中積累資訊，在後續步驟中根據已知資訊，動態選擇一致的最好求解路徑。

      6.分支限界法：可以看作搜尋方法的一種改良形式。

  • 常量因子和演算法複雜度

      大O記法：對於單調的整數函式f，如果存在一個整數函式g和實常數c > 0,使得對於充分大的n總有f(n) >= c * g(n),就說函式g是f的一個漸進函式（忽略常量因子）,記為f(n) = O(g(n)).

      假設存在函式g，使得演算法A處理規模為n的問題例項所用的時間T(n) = O(g(n)),則成O(g(n))為演算法A的漸進時間複雜度，簡稱時間複雜度。演算法的空間複雜度S(n)的定義與此類似。

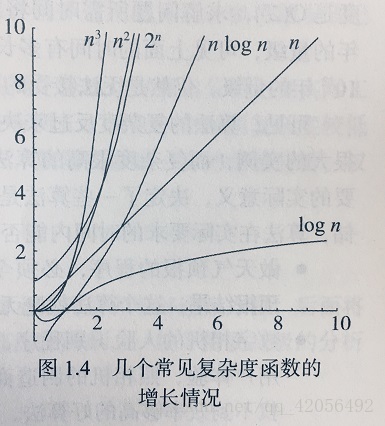
    演算法複雜度函式增長情況

  • 演算法分析    基本迴圈程式    0.基本操作，認為期時間複雜度為O(1)。如果函式呼叫，應該講其時間複雜度代入，參與整體時間複雜度的計算。

       1.加法規則。如果演算法是兩個部分的順序複合，其複雜度是這兩部分的複雜性之和。    T(n) = T1(n) + T2(n) = O(T1(n)) + O(T2(n)) = O(max(T1(n), T2(n)))

       2.乘法規則。如果演算法是一個迴圈，迴圈體將執行T1(n)次，每次執行需要T2(n)時間    T(n) = T1(n) x T2(n) = O(T1(n)) x O(T2(n)) = O(T1(n) x T2(n))

       3.取最大規則。如果演算法是條件分支，兩個分支的時間複雜性分別為T1(n) ， T2(n)    T(n) = O(max(T1(n), T2(n))))

• 資料結構

  • 資訊、資料和資料結構

     資料就是計算機能夠處理的符號形式的總和，或說是經過了編碼的資訊。

     資料元素指最基本的資料單位。

     資料結構是指研究據之間的關聯和組合的形式，總結其中的規律性，發覺特別值得注意的有用結構，研究這些結構的性質，進而研究如何在計算機裡實現這些有用的資料結構，以支援相應組合資料的高效使用，支援處理它們的高效演算法。

  • 抽象定義與重要類別   D = (E , R) 抽象地考慮資料結構的概念。從邏輯上看，一個數據結構包含一集資料元素，是一個有窮極，在這些元素之間有著某些特定的邏輯關係。其中E是資料結構D的元素集合，是某個資料集合 ε 的一個有窮子集，而R ∈ E x E 是D的元素之間的某種關係。

      典型的資料結構：

    集合結構、序列結構（線性結構、環形結構、p形結構）、層次結構、樹形結構、圖結構

  • 結構性和功能性的資料結構

      0.上述的序列結構、樹形結構、圖結構等稱之為結構性的資料結構

      1.支援元素儲存和訪問的資料結構被稱為容器

      2.功能性資料結構包括棧、佇列、優先佇列、字典等

  • 計算機記憶體物件表示

      程式中直接使用的資料儲存在計算機的記憶體儲器（簡稱記憶體）。記憶體是CPU可以直接訪問的資料儲存裝置。

      記憶體的基本結構是線性排列的一批儲存單元。一個單元可以儲存一個位元組（8位二進位制程式碼）的資料。

      記憶體單元具有唯一編號，成為單元地址，簡稱地址。64位計算機，一次可以存取8個位元組的資料，也就是說依次操作訪問8個單元的內容。O（1）操作。

第三部分：練習

.  

• 一般練習

     1.設法證明求平方根的牛頓迭代法一定收斂。    證明：   由定理知：假設f(x)在x的某領域內具有連續的二階導數，且設f(x) = 0, f′(x*) ≠ 0, 則對充分靠近x的初始值x0，牛頓迭代法產生的序列{xn}收斂於x。   求m的平方根等價於f(x) = x² - m = 0,f′(x) = 2x,應用與牛頓迭代法，得迭代計算格式為       x（n+1） = （x(n) + m/x(n)）/ 2,（n = 0, 1, 2,……）    所以說求平方根的牛頓迭代法一定收斂    2.修改紅綠燈安排例項中的演算法，使之最後給出的各個分組最大，可以考慮從本章演算法給出的分組出發，給每個分組加入不衝突的所有行駛方向。    解：得到{AB,ACAD,BA,DC,ED},{BC,BD,EA,BA,DC,ED},     {DA,DB,BA,DC,ED,AD},{EA,EB,BA,DC,ED,EA}    3.請完整寫出採用高斯消元法求矩陣行列式的演算法，並仔細分析其時間複雜度。    解：

#設被求值矩陣為二維表A[0:N][0:N]
for i in range(n-1):
	#A[i][i] 將A[i +1:n][i]的值都變為0
	for j in range(i+1, n):
		A[j][i] == 0
det = 0.0
for i in range(n):
	det += A[i][i]

  4.解決同一問題有兩種演算法，一個演算法的時間開銷約為100n³, 另一個約為0.5 x 2ⁿ。問題規模為多大的情況下後一演算法更快？      解：     100n³ = 0.5 x 2ⁿ      n>20之後後者演算法更快

  5.假設現在需要對全世界的人口做一些統計工作，希望在1天之內完成工作。如果採用的演算法具有線性複雜度，多快的計算機就足以滿足工作需求？如果所用演算法具有平方複雜度呢？用天河二號超級計算機大約能處理什麼複雜度的演算法？      解：     1天 = 86400秒，截止至2018年3月當今人口約75.9億。每秒878473次的計算機就能滿足工作要求。平方複雜度的每秒275500次的計算機就能滿足工作要求。天河二號超級計算機的平均速度為每秒3.39億億次，能處理指數及複雜度的演算法。      6.如果在宇宙大爆炸的那一刻啟動了一臺每秒十億次的計算機執行斐波那契數列的遞迴演算法，假設每條指令計算一次加法。到今天為止它可以算出第幾個斐波那契數？這個數的數值應該是多少？       解：     遞迴演算法難度級為O(n²)，宇宙大爆炸至今為138.2億年，約為4.3582752e+18秒，計算機計算至今已經計算了435827520次，因為難度級為n²，所以n約為20876。數值應該是。。。數值太恐怖了，還是不放了。。      7.假設你從3歲開始手工操作計算器每秒可以完成3次加法或乘法。執行斐波那契數的遞迴演算法，到今天為止你可能算出哪幾個斐波那契數？假設執行本章求矩陣乘積的演算法，到今天為止能做出兩個多大的矩陣的乘積？      解：     我今年21歲，姑且算他18年，約為567648000秒，沒日沒夜，無時無刻的算斐波那契數列，應該算了1702944000次，遞迴演算法難度級為O(n²)，所以我應該算了約41266次。具體算了什麼，我也不知道。矩陣乘積演算法難度級為O(n³)，我可能可以算出n = 1194大的矩陣的乘積。      8.根據本章的討論和自己的認識，設法對資料結構和演算法的關係做一個綜述和總結，並給出自己的認識，討論其中的問題。   

• 程式設計練習    1.請回憶（查閱）基礎數學中求平方根的方法。請定義一個Python函式，其中採用基礎數學中的方法求平方根。從各方面比較這個函式和基於牛頓迭代法的函式。      解：     基礎數學（筆算）一個平方數如下操作，因個人能力有限還是得用到math模組的sqrt方法，所以沒放上去。     ①．將被開方數的整數部分從個位起向左每隔兩位劃為一段，用撇號分開(豎式中的11’56)，分成幾段，表示所求平方根是幾位數；     ②．根據左邊第一段裡的數，求得平方根的最高位上的數(豎式中的3)；     ③．從第一段的數減去最高位上數的平方，在它們的差的右邊寫上第二段陣列成第一個餘數(豎式中的256)；     ④．把求得的最高位數乘以20去試除第一個餘數，所得的最大整數作為試商(3×20除 256，所得的最大整數是 4，即試商是4)；     ⑤．用商的最高位數的20倍加上這個試商再乘以試商．如果所得的積小於或等於餘數，試商就是平方根的第二位數；如果所得的積大於餘數，就把試商減小再試(豎式中(20×3＋4)×4＝256，說明試商4就是平方根的第二位數)；     ⑥．用同樣的方法，繼續求平方根的其他各位上的數．     相比之下，更能感受到牛頓迭代法帶來的簡易性。    2.基於1.3.4節中構造整數表的幾個函式做一些試驗，對一組引數值統計它們的執行時間。修改這些函式，重複試驗對Python中構造表的各種方法做一個總結。       程式碼如下：

import time

def test1(n):
    begin = time.time()
    lst = []
    for i in range(n*10000):
        lst = lst + [i]
    stop = time.time()
    print("test1消耗{}秒".format(stop-begin))



def test2(n):
    begin = time.time()
    lst = []
    for i in range(n*10000):
        lst.append(i)
    stop = time.time()
    print("test2消耗{}秒".format(stop - begin))


def test3(n):
    begin = time.time()
    lst = [i for i in range(n*10000)]
    stop = time.time()
    print("test3消耗{}秒".format(stop - begin))


def test4(n):
    begin = time.time()
    lst = list(range(n*10000))
    stop = time.time()
    print("test4消耗{}秒".format(stop - begin))


test1(10)
test2(10)
test3(10)
test4(10)

  顯示結果為   test1消耗41.73838710784912秒   test2消耗0.011000633239746094秒   test3消耗0.004000186920166016秒   test4消耗0.002000093460083008秒   因為test1的方法實在是不必要又耽誤時間，所以後面幾次我就沒有繼續使用test1方法。   當n取10000時   test2消耗62.904597759246826秒   test3消耗30.589749813079834秒   test4消耗16.711955785751343秒   顯然最後一個方法是最佳的，難度級也是最低的。test3花費的時間幾乎是test4的兩倍，test2約是test4的4倍。      3.用Python字典表示衝突圖結構，以關鍵碼（A, B）關聯的值為True表示衝突，沒有值表示不衝突，用這個技術完成本章求無衝突分組的程式。      這道題不知所云。。。是如關鍵碼（AB, BC）的關聯值還是什麼。。      4.基於前一題的類似設計，設法編寫一個程式，使之能枚舉出一個衝突圖上的各種分組組合，從中找出最佳的無衝分組。      不知所云+1   

第四部分：總結

  以上記錄的是自己學習的過程，課後練習也全是憑藉個人理解來完成的，正確答案以及方式有待商榷，如果有大神偶然看見小弟的這篇筆記，有不對的地方也懇請斧正，謝謝。