一.插入排序：

1、基本思想

直接插入排序的基本操作是將一個記錄插入到已經排好的有序表中，從而得到一個新的、記錄數增1的有序表。對於給定的一組記錄，初始時假定第一個記錄自成一個有序序列，其餘記錄為無序序列。接著從第二個記錄開始，按照記錄的大小依次將當前處理的記錄插入到其之前的有序序列中，直到最後一個記錄插到有序序列中為止。

2、複雜度分析

當最好的情況，也就是要排序的表本身就是有序的，此時只有資料比較，沒有資料移動，時間複雜度為O(n)。 當最壞的情況，即待排序的表是逆序的情況，此時需要比較次數為：2+3+…+n=(n+2)(n-1)/2 次,而記錄移動的最大值也達到了 (n+4)(n-1)/2

3、排序過程如下

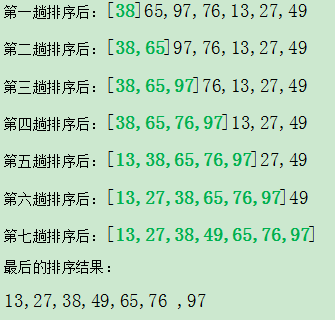
以陣列{38,65,97,76,13,27,49}為例， 

public class InsertSort {
    public static void insertSort(int[] a) {
        int i, j, insertNote;// 要插入的資料
        for (i = 1; i < a.length; i++) {// 從陣列的第二個元素開始迴圈將陣列中的元素插入
            insertNote = a[i];// 設定陣列中的第2個元素為第一次迴圈要插入的資料
            j = i - 1;
            while (j >= 0 && insertNote < a[j]) {
                a[j + 1] = a[j];// 如果要插入的元素小於第j個元素,就將第j個元素向後移動
                j--;
            }
            a[j + 1] = insertNote;// 直到要插入的元素不小於第j個元素,將insertNote插入到陣列中
        }
    }

    public static void main(String[] args) {
        int a[] = { 38,65,97,76,13,27,49 };
        insertSort(a);
        System.out.println(Arrays.toString(a));
    }
} 
 

二.希爾排序

1、基本思想：

希爾排序也成為“縮小增量排序”，其基本原理是，現將待排序的陣列元素分成多個子序列，使得每個子序列的元素個數相對較少，然後對各個子序列分別進行直接插入排序，待整個待排序列“基本有序”後，最後在對所有元素進行一次直接插入排序。因此，我們要採用跳躍分割的策略：將相距某個“增量”的記錄組成一個子序列，這樣才能保證在子序列內分別進行直接插入排序後得到的結果是基本有序而不是區域性有序。希爾排序是對直接插入排序演算法的優化和升級。 所謂的基本有序，就是小的關鍵字基本在前面，大的基本在後面，不大不小的基本在中間，例如｛2,1,3,6,4,7,5,8,9,｝就可以稱為基本有序了。但像｛1,5,9,3,7,8,2,4,6｝這樣，9在第三位，2在倒數第三位就談不上基本有序。

2、複雜度分析：

希爾排序的關鍵並不是隨便分組後各自排序，而是將相隔某個“增量”的記錄組成一個子序列，實現跳躍式移動，使得排序的效率提高。需要注意的是，增量序列的最後一個增量值必須等於1才行。另外，由於記錄是跳躍式的移動，希爾排序並不是一種穩定的排序演算法。 希爾排序最好時間複雜度和平均時間複雜度都是，最壞時間複雜度為。

3、排序過程如下：

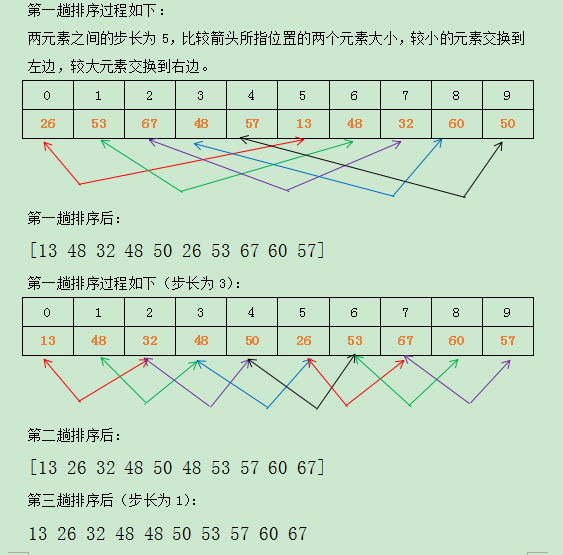
以陣列{26, 53, 67, 48, 57, 13, 48, 32, 60, 50 }為例，步長序列為{5,2,1} 初始化關鍵字： [26, 53, 67, 48, 57, 13, 48, 32, 60, 50 ]

最後的排序結果： 13 26 32 48 48 50 53 57 60 67

public static void shellSortSmallToBig(int[] data) {
        int j = 0;
        int temp = 0;
        for (int increment = data.length / 2; increment > 0; increment /= 2) {
            for (int i = increment; i < data.length; i++) {             
                temp = data[i];
                for (j = i - increment; j >= 0; j -= increment) {
                    if (temp < data[j]) {
                        data[j + increment] = data[j];
                    } else {
                        break;
                    }
                }
                data[j + increment] = temp;
            }
            for (int i = 0; i < data.length; i++)
                System.out.print(data[i] + " ");
        }
    }

    public static void main(String[] args) {
        int[] data = new int[] { 26, 53, 67, 48, 57, 13, 48, 32, 60, 50 };
        shellSortSmallToBig(data);
        System.out.println(Arrays.toString(data));
    }