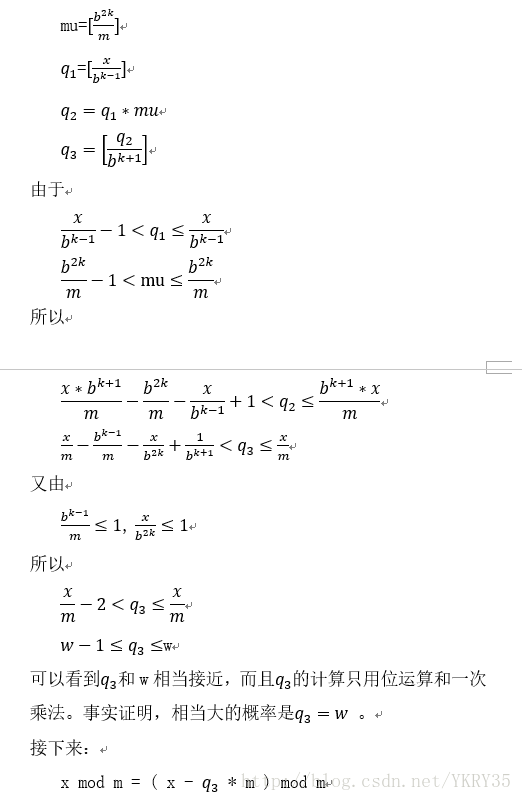大數取模運算,快速冪取模運算
1.快速冪取模
快速冪取模就是在O(logn)內求出a^n mod b的值。演算法的原理是ab mod c=(a mod c)(b mod c)mod c
long exp_mod(long a,long n,long b)
{
long t;
if(n==0) return 1%b;
if(n==1) return a%b;
t=exp_mod(a,n/2,b);
t=t*t%b;
if((n&1)==1) t=t*a%b;
return t;
}2.大數取模運算Barrett reduction
Barrett reduction演算法的證明和使用。
作者剛做完了課程設計作業,閒來無事寫篇文章。
大數中的指數運算,需要對一個數進行取模,因為最大可能二進位制下2048位的2048位次方,所以必須邊做乘法邊取模。
乘法使用快速冪,如果底數位數是x,指數位數是e,底數足夠大的話,複雜度取決於模數,模數是m位的話,複雜度是O(m*m*e)。程式裡,大數的儲存是2的32次方進位制的,這裡的m*m要除以(32*32)。
取模運算,如果直接呼叫大數取模,因為除法是很慢的,所以效率很低。用Barrett reduction演算法可以將除法轉化為乘法和位運算,減法。
因為模數是任意的,所以不用蒙哥馬利演算法。
作業裡只要求完成非負的大數運算,後面證明中預設大數都是非負的。
下面介紹Barrett reduction演算法
求 x mod m
m的位數是k
使用條件: x位數不大於2*k。對同一個數反覆取模。
使用方法(這裡是非負數):
計算常量 mu=b^2k / m
取模時:
q1 = x / b^(k-1)
q2 = q1 * mu
q3 = q2 / b^(k+1)
r1 = x % b^(k+1)
r2 = (q3 * m) % b^(k+1)
r = r1 - r2
if ( r > m ) r -= m
return r
很多資料把mu=b^2k / m寫成了mu=b^k / m,作者被坑了,很生氣,決定放假寫這麼一個文章。另外,百度上基本看不到什麼相關的證明。
證明:
[]表示取整,b是大數的進位制
只需要一次除法預處理。
之後的除法和取模都是對進位制b的若干次方進行的,所以位運算即可。
乘法時,因為最後結果是要取最後k+1位的,所以在乘的時候,可以直接把k+1位前面的丟棄,減少迴圈次數。作者是另外寫了一個限制位數的乘法函式,效率提升了一些。
證明部分截圖自word實驗報告。
大數取模:一般取模+技巧取模+快速冪取模+尤拉函式(費馬小定理)
https://blog.csdn.net/u011361880/article/details/77802742
一般取模運算(不推薦):
(a^n)%m。 我們可以改寫為(a^n)%m= ((a%m)^n)%m, 即迴圈n次。
缺點:低效,迴圈了n次。
int exp_mod(int a,int n,int m){
a = a%m;
int temp = 1;
while(n--)
{
temp = temp * a;
temp = temp % m;
}
return temp;
}第一種,技巧取模:
(a^n)%10
當n非常大時,嗯,只能用字串存n的時候。
簡單分析一下,
a%10. 有10種可能,(來源於室友“張博士”的逆天發現,明明可以靠臉吃飯,他偏偏要靠才華,明明可以快速冪取模,它偏要發現這種,出現大大大大數的)
a%10 = 0. 這個結果就不需要看了。0
a%10 = 1. (1^n )%10會出現的可能數字:1
a%10 = 2. (2^n )%10會出現的可能數字:2,4(=2*2), 8(=2*4),6(=2*8),繼續迴圈,2, 4, 8, 6…..
a%10 = 3. (3^n )%10會出現的可能數字:3,9(=3*3),7(=3*9), 1(=3*7),繼續迴圈,3,9,7,1…..
a%10 = 4. (4^n )%10會出現的可能數字:4,6(4*4) , 繼續迴圈,4,6……
a%10 = 5. (5^n )%10會出現的可能數字:5
a%10 = 6. (6^n )%10會出現的可能數字:6
a%10 = 7. (7^n )%10會出現的可能數字:7, 9, 3, 1 繼續迴圈,
a%10 = 8. (8^n )%10會出現的可能數字:8, 4, 2, 6 繼續迴圈,
a%10 = 9. (9^n )%10會出現的可能數字:9, 1 繼續迴圈,
重點是繼續迴圈,發現,最大情況下,都是以4位數字迴圈,換句話說,(a^n)%10 和(a^(n+4))%10是相等的,當然,這裡n不等於0. 如果這裡看懂了,那這裡差不多就ok了。
我們把n –> (n%4)+4. 這裡加4的原因是為了防止n%4==0. ,並且我們沒有考慮n==0的情況。這個單獨處理一下。
OK
如果n != 0.
(a^n)%10 = (a^(n%4+4))%10 = ((a%10)^(n%4+4)) % 10
另外友情提示:對於n,如果是字串儲存,(十進位制) 我們只需要取最後的2位數,用它代替n即可,因為999, 900肯定是可以被4整除的,我們只需要99即可,用99%4+4。
如果是int 型或longlong。(二進位制) (n & 11)按位“與”可以取出後2位,代替n%4,(注意不能代替n%4+4 . 加4一直需要),第3位是4,肯定可以被4整除。
(a^n) %b
long exp_mod(long a,long n,long b)
{
long t;
if(n==0) return 1%b;
if(n==1) return a%b;
t=exp_mod(a,n/2,b);
t=t*t%b;
if((n&1)==1) t=t*a%b;
return t;
}這個程式碼就是一般的折半,遞迴,折半….。注意,(n&1) 按位“與 ”,如果是奇數,那麼結果是1,否則結果是0.
(a^n) %b
int exp_mod(int a,int b,int n){
int r=1;
while(b){
if(b&1)r=(r*a)%n;
a=(a*a)%n;
b>>=1; // b = b>>1;
}
return r;
}主要思想還是折半。但是運用的非常巧妙,假設b是一個偶數,並且b/2.b/4,b/8.。。。。一直到2都是偶數,
OK,假設b == 16. a==2.
b = 16,8,4,2,1
我們發現,只有最後一次,b==1,時,我們進入了if語句,
我們檢視while迴圈裡面,a的變化。(這裡先不考慮模)
b=16,進入while a = 2^2;
b=8, a = 2^4;
b=4, a = 2^8;
b=2, a = 2^16
b=1, ,進入if語句,r = a, 此時返回的是r。
假設b=18.
b=18,進入while a = 2^2;
b=9, 此時,進入了if語句。r=2^2. a = 2^4;
b=4, a = 2^8;
b=2, a = 2^16
b=1, ,進入if語句,r = r*a = 2^2 * 2^16 , 此時返回的是r。
我們發現,在b=9時,我們用r儲存了2^2. 為什麼呢。反過來,從下往上看,我們要計算2^18次方。但是我們此時只知道2^8的結果,我們並不知道2^9是多少。因此,我們用了2個2^8. 此時,我們還是差了一個2^2.
r儲存的剛好是這個值。
當b是奇數時。b越小,說明離18越遠,從下往上乘,我們一開始是差一個2(b=8和b=9差一個2),一直往上翻倍,即到了18,差2個2.即2^2。因此,r的值也需要越來越大。 (這裡需要好好理解。)
每碰到一次奇數,我們都會和原來的差一個2. 然後這個奇數距離18的距離越遠。我們需要補回去的值就越大,即r的值。
重新舉一個例子:
b=22 進入while a = 2^2
b=11 進入if,r = 2^2. a=2^4 ——>要補回2^2
b=5 進入if, r=2^2 * 2^4. a = 2^8 ——> 要補回2^4
b=2 a=2^16
b=1,進入if, r = 2^2 * 2^4 * 2^16
當b=11時,只知道2^5,用了兩個,可以變成2^10.
和11相差一個2.再到22即相差兩個2.
當b=5時,只知道2^2.用了兩個。可以變成2^4,相差一個2. 再到10(11)時,翻倍,變成了2個。
(10到11,在b=11那裡已經補回來了),再到22,翻倍,變成2個。
第三種,尤拉函式:
先介紹一個定義,互質:a和b互質,即a和b除了1以為,沒有其他公約數。
對正整數n,尤拉函式是小於n的數中與n 互質的數的數目,
φ(8)=4,因為1,3,5,7均和8互質。
費馬小定理:
對於互質的整數a和n,有a^φ(n) ≡ 1 mod n
即(a^φ(n)) % n = 1 %n = 1;
我們常常會見到。求(a^n)%1000000007, n>1000000007.
因為m=1000000007是質數,毫無疑問,φ(m) = m-1 = 1000000006.
假設n = k * 1000000006 +r .其中r是餘數,
我們利用費馬小定理降級處理。
(a^n)%1000000007 = (a^( k * 1000000006 +r ))%1000000007
=(a^( k * 1000000006 ))%1000000007 * (a^r )%1000000007
=1 * (a^r )%1000000007
直接把n變成了r。