01第一章、神經網路任何工作 1.1到1.8
第 1 章、神經網路如何工作
1.1、尺有所短,寸有所長
計算機和人的關係:尺有所短,寸有所長 有些任務,對傳統的計算機而言很容易,對人類而言卻很難。例如,對數百萬個數字進行乘法運算。 另一方面,有些任務對傳統的計算機而言很難,對人類而言卻很容易。例如,從一群人的照片中識別出面孔。
1.2、一臺簡單的預測
1、思想過程
人類:問題->思考->答案 計算機:輸入->流程(計算)->輸出 計算機的例項:輸入(3*4)->流程(4+4+4)->輸出(12) 所有有用的計算機系統都有一個輸入和一個輸出,並在輸入和輸出之間進行某種型別的計算。神經網路也是如此。
2、案例
一個預測案例:千米和英里的轉換 計算機:輸入(千米)->流程(?)->輸出(英里) 已知:千米和英里之間的關係是線性的。(這裡,“線性的”被叫做模型) 一些線索:0千米=0英里 100千米=62.137英里 所以,假設流程是英里=千米*C(根據“線性的”模型得到的公式) 假設C=0.5,得到100千米=50英里,和目標62.137英里差距是12.137,這個12.137被叫做誤差。 然後,修改引數值,0.5變成0.6,100千米=60英里,和目標62.137英里差距是2.137,現在這個誤差比之前好多了。 然後,修改引數值,0.6變成0.7,100千米=70英里,和目標62.137英里差距是-7.863,這個誤差的負號告訴我們,我們超調了。 那麼我們將引數值變成0.61,100千米=61英里,和目標62.137英里差距是1.137,現在這個誤差比之前好多了,這改變引數的方法,叫做學習率,在梯度下降法中又叫步長。
3、啟發
通過預測案例得到的啟發 誤差的大小指導如何改變引數C的值。 大誤差意味著大的修正值,小誤差意味著小的修正值。 迭代:嘗試得到一個答案,並多次改進答案,這是種方法叫做迭代。 當我們不能精確知道一些事情如何運作時,我們可以嘗試使用模型來估計其運作方式,在模型中,包括了我們可以調整的引數。如果我們不知道如何將千米轉換為英里,那麼我們可以使用線性函式作為模型,並使用可調節的梯度值作為引數。 改進這些模型中引數的一種好方法是,基於模型和已知真實示例之間的比較,得到模型偏移的誤差值,調整引數。 選擇正確的模型很重要。
1.3、分類器與預測器並無太大差別
預測器:機器接受了一個輸入,並作出應有的預測,輸出結果。
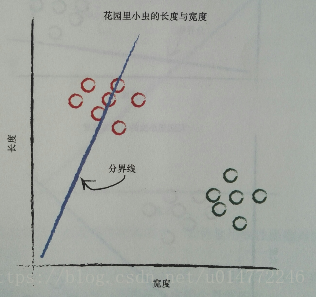
書中舉了個根據長度和寬度分類花園裡毛蟲和瓢蟲的案例。
因為毛蟲細而長,瓢蟲短而寬,所以可以用一條線來分開。
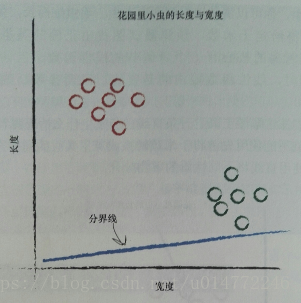
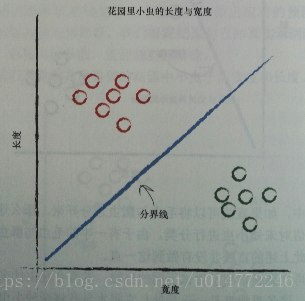 在修改這條線的過程中,用預測器來做引數的改變,其實也就是分類。
所以,分類器和預測期並沒有太大差別,機制都是一樣的。
在修改這條線的過程中,用預測器來做引數的改變,其實也就是分類。
所以,分類器和預測期並沒有太大差別,機制都是一樣的。
1.4、訓練簡單的分類
1、例子引入
根據一個數據來設定分割線的例子講解:
還是之前1.3的分類毛蟲和瓢蟲的問題。
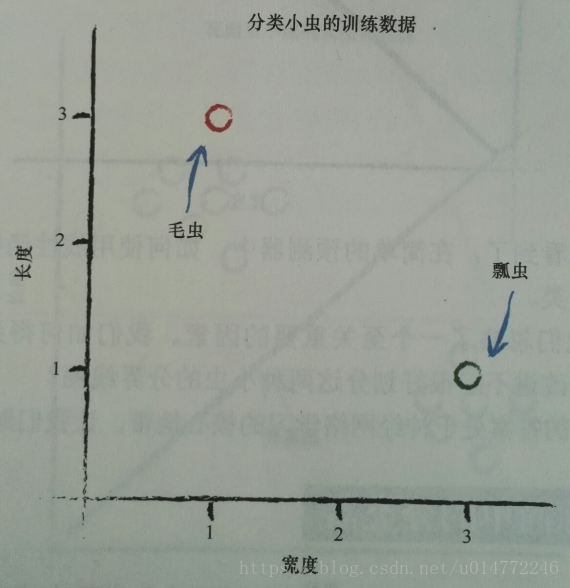
假設模型為線性的,分界線函式為y=Ax,長度為y,寬度為x。
已知有兩個例項:
瓢蟲:寬3.0 長:1.0
毛蟲:寬1.0 長:3.0
即:
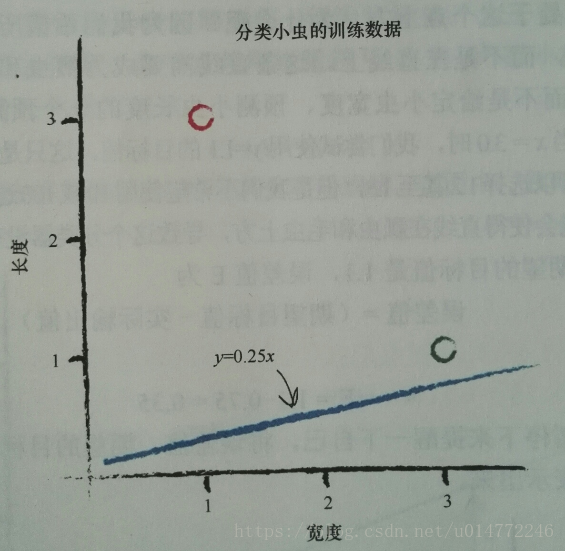
2、改進
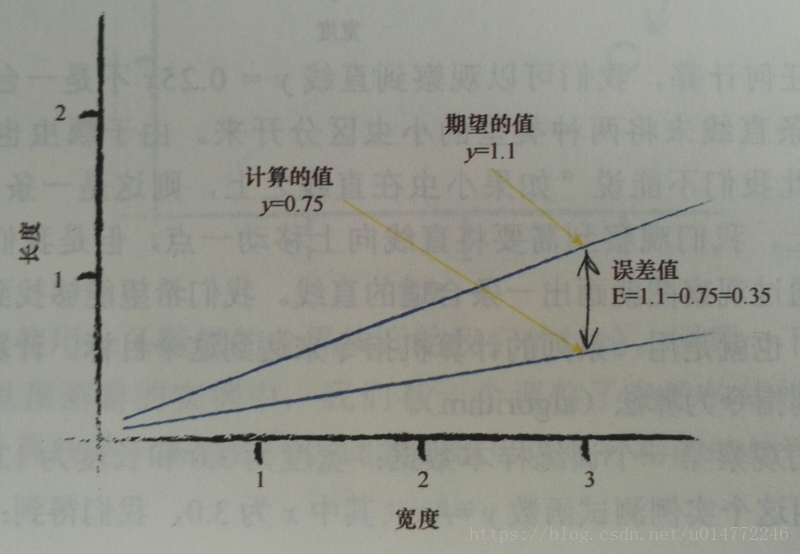
機器學習的一個重要思路,我們應該進行適度改進(moderate),即我們不要改進的過於激烈。也就是說不要一下子將本次的A改進到目標的A。 這種自我節制的調整,還帶來了一個非常強大、行之有效的“副作用”。當訓練資料本身不能確信為完全正確並且包含在現實世界測量中普遍出現的錯誤或噪聲這兩種情況時,有節制的調整可以抑制這些錯誤或噪聲的影響。這種方法使得錯誤或噪聲得到了調解和緩和。 這次,我們新增一個調劑係數:ΔA=L* (E/x),假設L=0.5,第一次訓練,x=3.0,A=0.25,y=0.253.0=0.75,期望值為1.1,得到了誤差值E為0.35,ΔA=L (E/x)=0.0583,更新後的A為0.25+0. 0583=0.3083。 使用更新後的A進行第二次訓練,x=3.0,A=0.3083,y=0. 3083*3.0=0.9250,期望值為小於1.1,雖然還是錯誤的,但是再進行多次訓練,總能正確,因為這條直線確實向正確的方向移動了。
3、結論
我們使用簡單的數學,理解了線性分類器輸出誤差值和可調節斜率引數之間的關係。也就是說,我們知道了在何種程度上調整斜率,可以消除輸出誤差值。 使用樸素的調整方法會出現一個問題,即改進後的模型只與最後一次訓練樣本最匹配,“有效地”忽略了所有以前的訓練樣本。解決這個問題的一種好方法是使用學習率:調節改進速率,這樣單一的訓練樣本就不能主導整個學習過程。 來自真實世界的訓練樣本可能充滿噪聲或包含錯誤。適度更新有助於限制這些錯誤樣本的影響。
1.5、有時候一個分類器不足以求解問題
如果資料本身不是由單一線性過程支配,那麼一個簡單的線性分器不能對資料進行劃分。例如,由邏輯XOR運算子支配的資料明瞭這一點。
但是解決方案很容易,你只需要使用多個線性分類器來劃分由單直線無法分離的資料。
比如,邏輯and運算的分類,一個分類器解決問題:
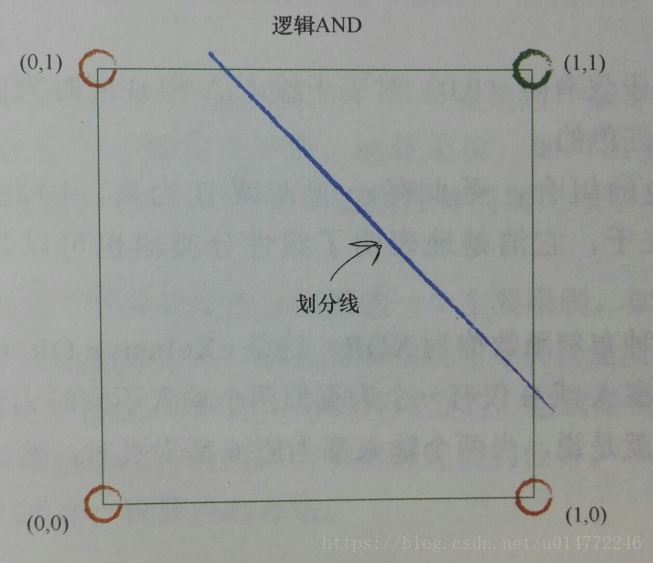
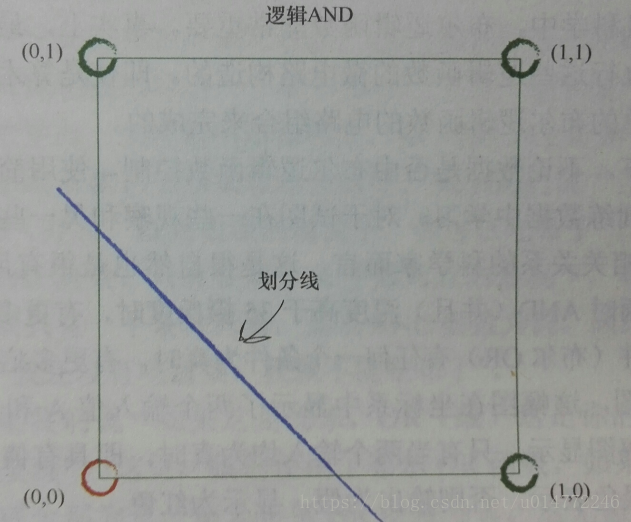
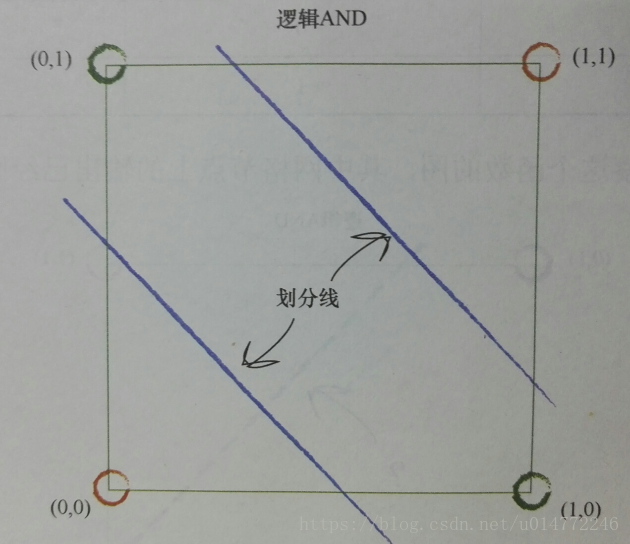
1.6、神經元——大自然的計算機器
1、神經元的結構
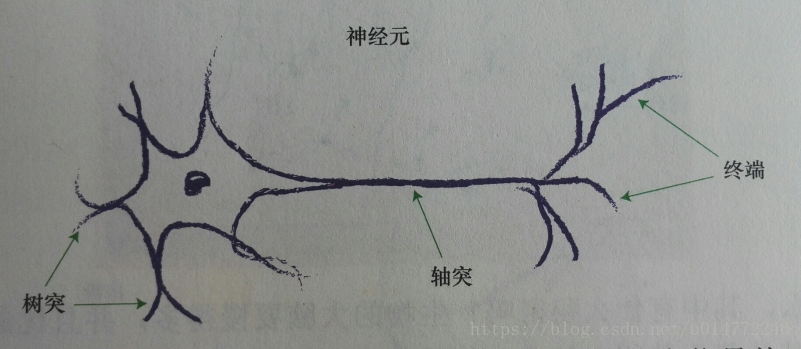
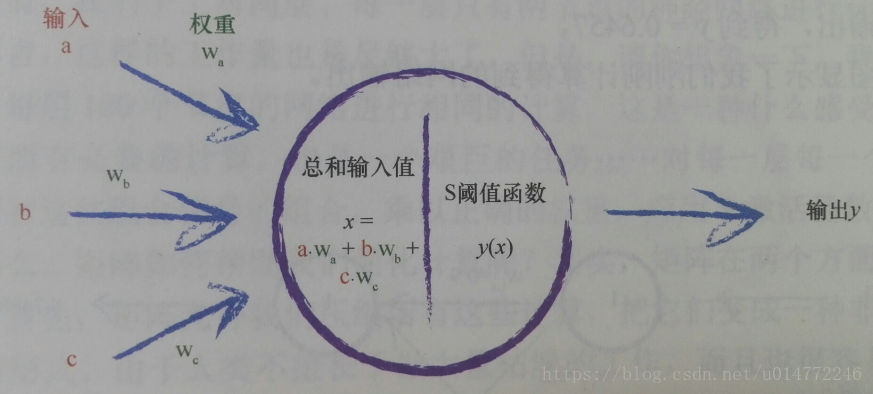
2、閾值(threshold)
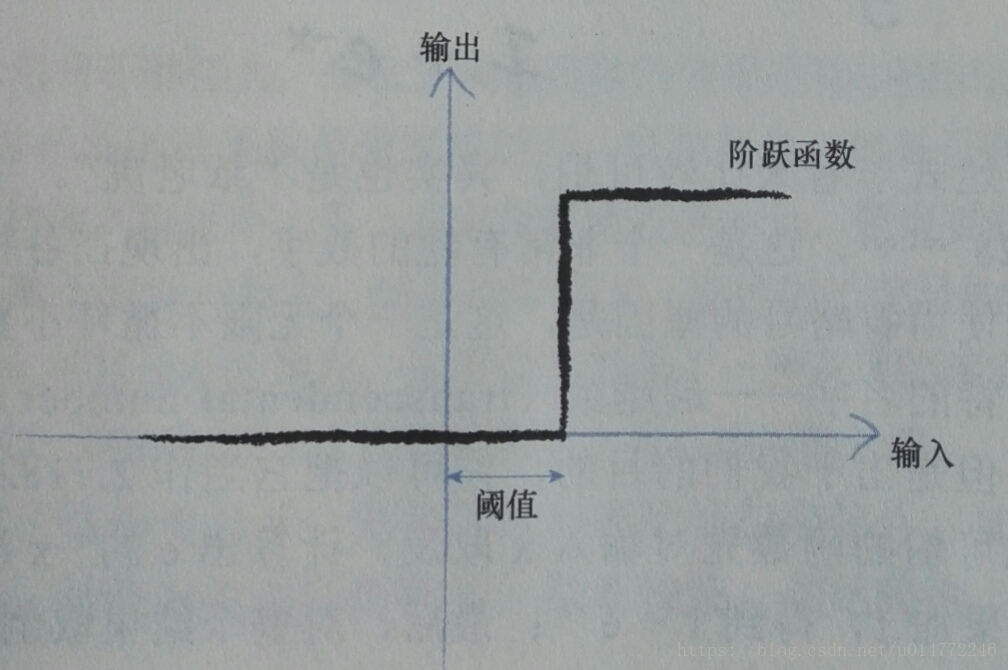
觀察表明:神經元不會立即反應,而是會抑制輸入,直到輸入增強,強大到可以觸發輸出。一些簡單的階躍函式可以實現這種效果,如下圖所示:

3、輸入問題
現在,整理一下整個神經元的模擬結果,如下圖所示:
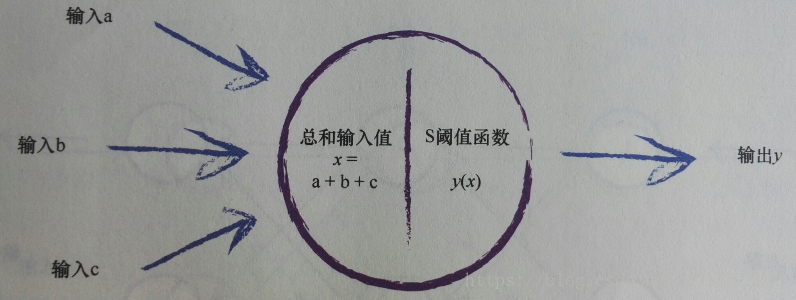
4、權重
本來神經元的結構如下所示:
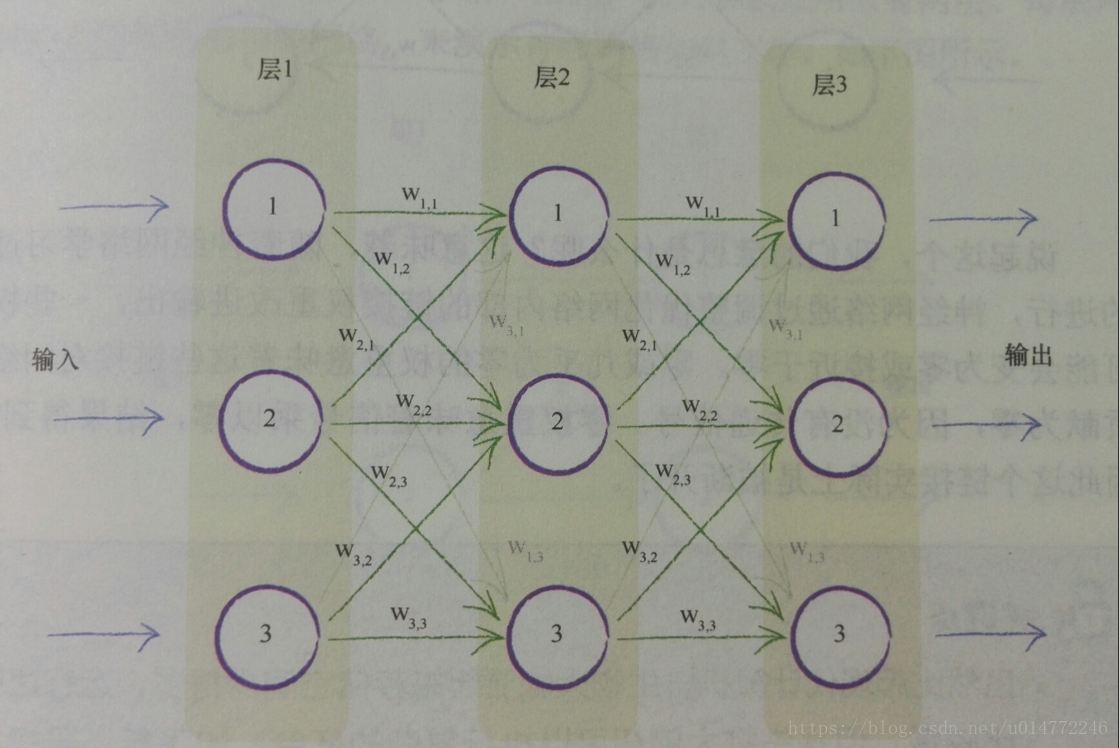
1.7、在神經網路中追蹤訊號
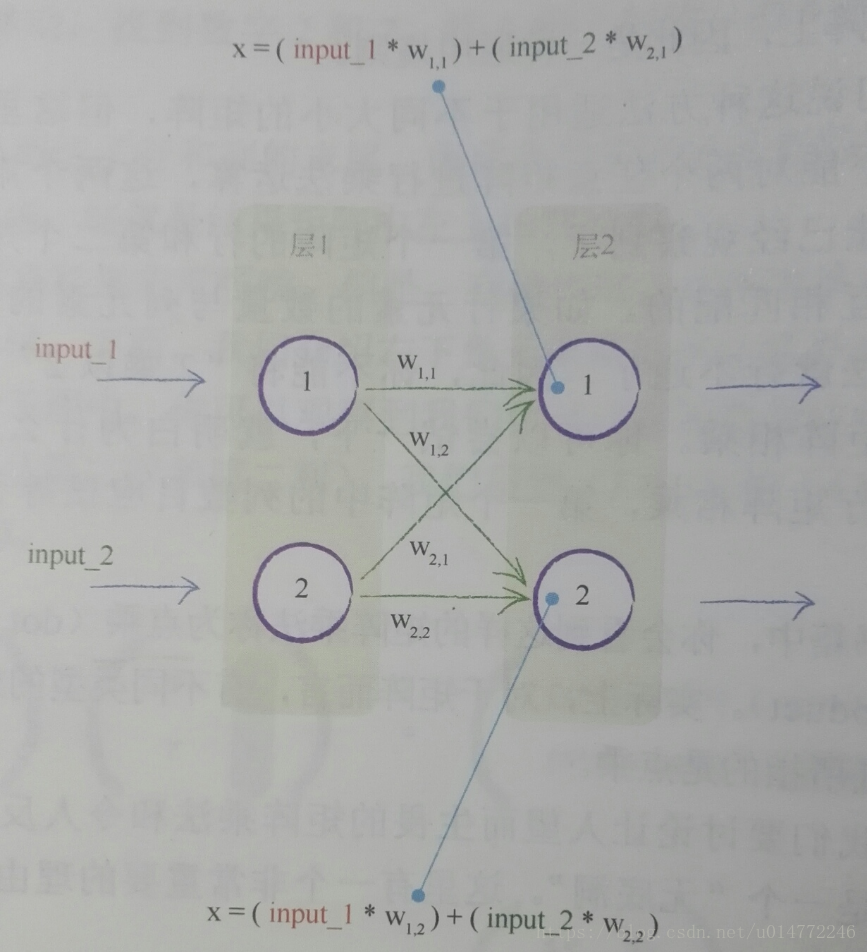
本節模擬了輸入如何在神經網路中變成輸出的過程。使用的是一個很簡單的神經網路。
如下圖,一個簡單的神經網路示意圖,兩個輸入分別為1.0和0.5,四個權重也已經標在了圖上。
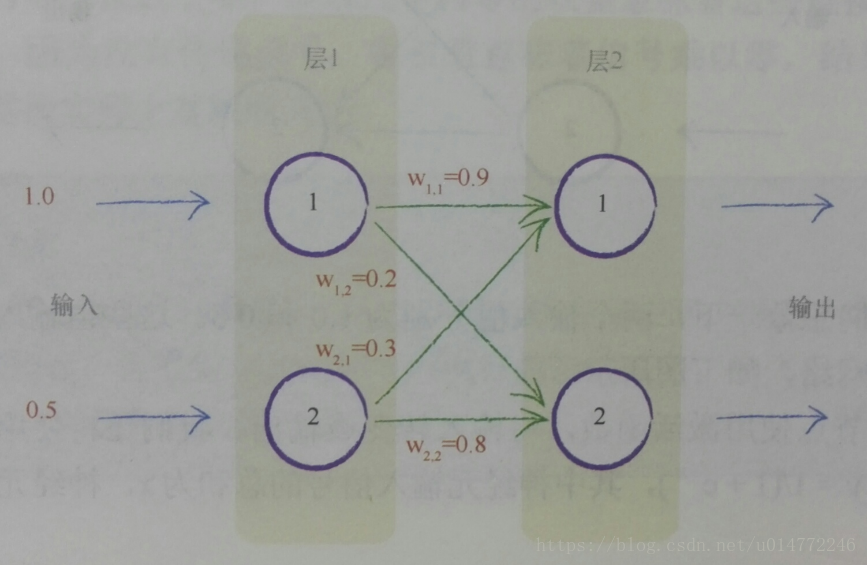
1.8、憑心而論,矩陣乘法大有用途
本節用大量的語音解釋了矩陣的點乘的原理,這裡我就不詳細記錄了,都是學過好幾遍的東西。
重點記錄一下關於神經網路的東西。
對於上一節所描述的計算,假設有權值矩陣和輸入值矩陣,並將其做點乘運算,將會得到如下結果:
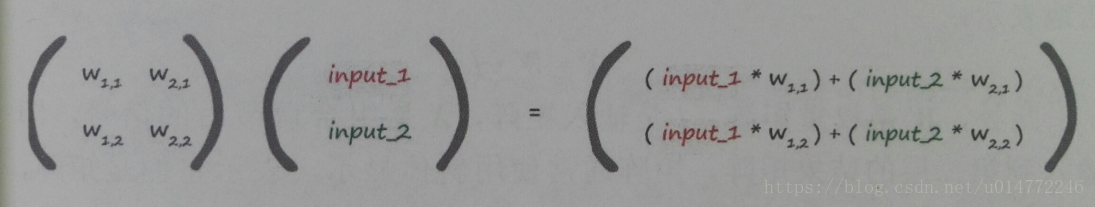
另:一些說明 1、本部落格僅用於學習交流,歡迎大家瞧瞧看看,為了方便大家學習。 2、如果原作者認為侵權,請及時聯絡我,我的qq是244509154,郵箱是[email protected],我會及時刪除侵權文章。 3、我的文章大家如果覺得對您有幫助或者您喜歡,請您在轉載的時候請註明來源,不管是我的還是其他原作者,我希望這些有用的文章的作者能被大家記住。 4、最後希望大家多多的交流,提高自己,從而對社會和自己創造更大的價值。