近期拜讀了Jo ̃ao F. Henrique大神的KCF論文，該論文在IEEE2014發表，在2015年公開了Matlab與C版本的程式碼（資料集為OTB-50、OTB-100，在Matlab R2016b版本中，將程式碼中的show_video.m的第24行的Number改為NumberTitle，即可跑通）。

下面是對該論文的詳細介紹。

摘要

如今大多數跟蹤器的核心元件是判別分類器，其任務是區分目標和周圍環境。為了適應自然影象變化，通常使用經過轉化和縮放的樣本塊來訓練該分類器。這樣的樣本集充滿了冗餘 --- 任何重疊的畫素都被限制為相同。基於這個簡單的觀察，我們提出了數千個轉化塊的資料集分析模型。通過顯示結果資料矩陣是迴圈的，我們可以使用離散傅立葉變換對其進行對角化，從而將儲存和計算減少幾個數量級。有趣的是，對於線性迴歸，我們的公式相當於一些最快競爭的跟蹤器使用的相關濾波器。而對於核迴歸，我們推匯出一種新的核化相關濾波器（KCF），與其他核算法不同，它具有與線性對應物完全相同的複雜度。在此基礎上，我們還提出了一種線性相關濾波器的快速多通道擴充套件，通過線性核，我們稱之為對偶相關濾波器（DCF）。 KCF和DCF在50個視訊基準測試中的表現優於Struck或TLD等頂級跟蹤器，儘管每秒執行數百幀，並且只需幾行程式碼即可實現（演算法1）。為了鼓勵進一步的發展，我們的跟蹤框架是開源的。

1 介紹

可以說，最近視覺跟蹤研究中最大的突破之一是判別學習方法的廣泛採用。跟蹤任務是許多計算機視覺系統的關鍵組成部分，可以自然地指定為線上學習問題[1]，[2]。給定包含目標的初始影象塊，目標是訓練學習一個分類器以區分目標和周圍環境。該分類器可以在許多位置進行精細評估，以便在後續幀中檢測它。當然，每個新檢測都提供了一個新的影象塊從而更新模型。

我們很容易專注於表徵感興趣的目標物件 - 分類器的正樣本。然而，判別方法的核心原則是給予同樣或者更多的相關環境 -- 即負樣本。最常用的負樣本是來自不同位置和尺度的影象塊，它反映了在這些條件下評估分類器的先驗知識。

一個極具挑戰性的因素是可以從影象中獲得幾乎無限量的負樣本。由於跟蹤的時間敏感性，如今的跟蹤器在儘可能多地合併樣本和保持較低的計算需求之間保持得很好。通常的做法是每幀隨機選擇幾個樣本[3]，[4]，[5]，[6]，[7]。

雖然這樣做的原因是可以理解的，但我們認為負樣本的欠取樣是阻礙跟蹤績效的主要因素。在本文中，作者開發了用於在不同的相對平移下分析地合併數千個樣本的工具，而無需明確地迭代它們。這可以通過以下發現來實現：在傅立葉域中，如果我們使用特定的模型進行轉換，一些學習演算法實際上變得更容易。

這些分析工具，即迴圈矩陣，在流行的學習演算法和經典訊號處理之間提供了有用的橋樑。這意味著我們能夠提出一種基於Kernel的脊迴歸[8]的跟蹤器，它不會受到“核詛咒”的影響，它有較大的漸近複雜度，甚至比非結構化線性迴歸表現出更低的複雜性。而且它可以被視為線性相關濾波器的核化版本，它構成了可用的最快跟蹤器的基礎[9]，[10]。我們利用與線性相關濾波器相同的計算複雜度的強大核心技巧。我們的框架輕鬆地包含多個特徵通道，並且通過使用線性核心，我們展示了線性相關濾波器到多通道情況的快速擴充套件。

2 前期工作

2.1 跟蹤檢測方面

對檢測跟蹤的全面回顧超出了本文的範圍，但我們將感興趣的文章引用到兩個極好的和最近的調查[1]，[2]。最流行的方法是使用判別性外觀模型[3]，[4]，[5]，[6]。受統計機器學習方法的啟發，它包含了線上訓練分類器，來預測影象塊中目標的存在與否。然後在許多候選塊上測試該分類器從而找到最可能的位置。或者，也可以直接預測位置[7]。使用類標籤的迴歸可以看作是分類，因此我們可以互換地使用這兩個術語。

在關注與我們的分析方法更直接相關的文獻之前，我們將討論一些相關的跟蹤器。逐個檢測範例的典型例子包括基於支援向量機（SVM）[12]，隨機森林分類器[6]或弱分類變體[13]，[5]。為了對跟蹤有用，所有提到的演算法都適用於線上學習。張等人[3]提出了一個固定隨機基礎的投影，以受壓縮感測技術的啟發來訓練樸素貝葉斯分類器。為了直接預測目標的位置，而不是在給定的影象塊中進行選取，Hare等人[7]基於大量的影象特徵，採用了結構化輸出SVM和高斯核。非判別性跟蹤器的例子包括Wu等人的工作[14]，他們將跟蹤描述為一系列影象對齊目標。以及Sevilla-Lara和Learned-Miller [15]，他們提出了一個基於分佈領域的強外觀描述符。 Kalal等人[4]的另一種判別性方法使用一組結構約束來指導增強分類器的取樣過程。最後，Bolme等人[9]採用經典訊號處理分析來推導快速相關濾波器。我們將在稍後更詳細地討論最後這兩個的文章。

2.2 樣本轉換與相關濾波

回想一下，我們的目標是有效地學習和檢測轉換的影象塊。與我們的方法不同，到目前為止，大多數嘗試都集中在試圖清除不相關的影象塊。在檢測方面，可以使用分支定界來找到分類器響應的最大值，同時避免不希望的候選塊[16]。不幸的是，在最壞的情況下，演算法可能仍然需要迭代所有影象塊。相關方法可以有效地找到一對影象中最相似的色塊[17]，但不會直接轉換為我們的設定。雖然它並不排除詳盡的搜尋。但值得注意的是，使用快速但不準確的分類器來選擇有可能的塊，並且只在那些[18]，[19]上應用完整但較慢的分類器。

在訓練方面，Kalal等人[4]提出，使用結構約束從每個新影象中選擇相關的樣本塊。這種方法相對昂貴，限制了可以使用的特徵，並且需要仔細調整結構啟發式；另一種流行的相關方法雖然主要用於離線檢測學習，即負樣本挖掘[20]。它包括在影象池上執行初始檢測器，並選擇任何錯誤的檢測作為重新訓練的樣本。儘管兩種方法都減少了訓練樣本的數量，但主要缺點是必須通過執行檢測器來考慮候選塊。

我們研究方向的最初動機是在跟蹤中近期成功的相關濾波器的應用[9]，[10]。事實證明，相關濾波器與更復雜的方法相比具有競爭力，但僅使用一小部分計算能力，數百幀/秒。他們利用了這樣一個事實，即兩個影象塊的卷積（鬆散地，它們在不同相對轉換中的點積）相當於傅立葉域中的元素乘積。因此，通過在傅立葉域中制定它們的目標，它們可以一次性指定用於若干平移或影象移位的線性分類器的期望輸出。

從[21]中可以看出，在訊號處理方面有數十年的研究中，傅立葉域方法可以非常有效。不幸的是，它也可能是非常有限的。我們希望，在傅立葉域上，同時利用計算機視覺方面的最新進展，例如更強大的功能，大邊緣分類器和核方法[22]，[20]，[23]。

一些研究正朝該方向發展，並嘗試將核方法應用於相關濾波器中[24]，[25]，[26]，[27]。在這些工作中，必須區分兩種型別的目標函式：一種是不考慮功率譜或影象轉換，例如合成判別函式（SDF）濾波器[25]，[26]，以及另一種，即考慮功率譜或影象轉換，例如最小平均相關能量[28]，最佳權衡[27]和最小平方誤差輸出和（MOSSE）濾波器[9]。由於可以有效地忽略空間結構，前者更容易核化，並且已經提出了核SDF濾波器[26]，[27]，[25]。然而，在影象轉換方面，由於缺乏非線性核和傅立葉域之間的相關性，將核技巧應用於其他濾波器更困難[25]，[24]，他們提出需要更高的計算時間和影象偏移數量的限制[24]。

這提示我們需要在影象塊轉換和訓練演算法之間建立更深層次的聯絡，以克服傅立葉域公式的侷限性。

圖1.與效能最佳的Struck和TLD相比，作者提出的核心相關濾波器（KCF）的結果。在HOG特徵上選擇的是高斯核，上述截圖是在最近的基準測試的50個視訊中擷取的[11]。丟失的跟蹤器用“x”表示。 KCF優於Struck和TLD，其實現最少且執行速度為172 FPS。

2.3 後續工作

自從這項工作的初始版本[29]以來，所提出的迴圈移位模型的一個有趣的時域變體已經非常成功地用於視訊檢索[30]。還提出了線性相關濾波器到多通道的推廣[31]，[32]，[33]，其中的一些是基於我們的初始版本。這允許他們利用更現代的特徵（例如，方向梯度直方圖 - HOG）。還提出了對其他線性演算法的推廣，例如支援向量迴歸[31]。這裡必須指出，所有這些工作都以離線訓練為目標，因此依賴於較慢的求解器[31]，[32]，[33]。相比之下，我們專注於快速元素操作，甚至使用核技巧，它也更適合實時跟蹤。

3 貢獻

早期提出了這項工作的初級版本[29]。它首次證明了帶有迴圈移位樣本的脊迴歸和經典相關濾波器之間的聯絡。這使得用 $O(n\log n )$ 快速傅立葉變換的快速學習代替了昂貴的矩陣代數。還提出了第一個核相關濾波器，但僅限於單個通道。還提出了在所有迴圈移位中計算核的封閉式解決方案。它們具有相同的 $O(n\log n )$ 計算成本，並且是針對徑向基和點積核匯出的。

目前的工作是在初始版本基礎上增加了重要的方法：（1）使用更簡單的對角化技術重新匯出所有原始結果（第4-6節）。（2）我們將原始工作擴充套件到多通道，這就讓我們使用最先進的特徵來顯著提升效能（第7節）。（3）在初始工作中添加了大量新分析和直觀解釋。（4）我們還將原始實驗從12個視訊擴充套件到50個視訊，並添加了基於方向梯度直方圖（HOG）特徵而非原始畫素的核相關濾波器（KCF）跟蹤器的新變體。（5）通過線性核，我們還提出了一種計算複雜度非常低的線性多通道濾波器，幾乎與非線性核心的效能相匹配。我們將其命名為對偶相關濾波器（DCF），並展示了它與一組最近更昂貴的多通道濾波器的關係[31]。在實驗上，我們證明了在沒有任何特徵提取的情況下，KCF已經比線性濾波器表現更好。憑藉HOG功能，線性DCF和非線性KCF都可以在Struck [7]或Track-Learn-Detect（TLD）[4]等大型頂級跟蹤器表現出色，同時可以在數百幀每秒的情況下輕鬆執行。

4 模組

在本節中，我們提出了在不同平移下提取影象塊的分析模型，並計算出對線性迴歸演算法的影響。我們將展示與經典相關濾波器的自然底層連線，這將允許我們在第5-7節中研究更復雜的演算法。

4.1 線性迴歸

由於脊迴歸展現了一個簡單的閉合式解決方案，並且可以實現接近更復雜方法的效能，例如支援向量機[8]。訓練階段，我們需要找到一個函式 $f(z)={w}^{T}z$ ，使得平方誤差達到最小值，即

其中， $x_{i}$ 為樣本， $y_{i}$ 為所迴歸的目標， $\lambda$ 為如同SVM中的控制過擬合的正則化引數。

文獻[8]中給出了 $w$ 的閉合形式 $w=(X^{T}X+\lambda I)^{-1}X^{T}y$ （2），由於在本文的4.4節中提出要在傅立葉域中進行運算，通常會出現複數值，故將 $w$ 轉換為複數域：

$w=(X^{H}X+\lambda I)^{-1}X^{H}y$ （3）

其中， $X^{H}={X^{*}}^{T}$ 為厄米特轉置。可以看到，由於涉及矩陣的求逆等複雜操作，從而使得計算複雜度過高。

4.2 迴圈移位

我們首先討論一下一維單通道訊號，之後在第7節將推廣至二維多通道影象。作者將 $n$ 維列向量 $x$ 作為基礎樣本，目的是使用基本樣本（一個正樣本）和通過轉換獲得的幾個虛擬樣本（即負樣本）來訓練一個分類器。我們可以通過迴圈移位運算元 $P$ 來建模該向量 $x$ 的一維轉換，迴圈移位運算元 $P$ 是置換矩陣。

那麼 $Px=\left [ x_{n} ,x_{1},x_{2},...,x_{n-1}\right ]^{T}$ 表示向量 $x$ 的元素向右平移一個單位。

上圖表示了 $n$ 維列向量 $x$ 組成的 $n\times n$ 維迴圈矩陣 $C(x)$ ，由於迴圈特性，我們每 $n$ 個週期定期得到相同的訊號 $x$ 。這意味著可以獲得整個移位訊號，即有：

$\left \{ P^{u}X|u=0,...,n-1 \right \}$ （5）

4.3 迴圈矩陣<增加樣本數>

由上節分析可知， $X=C(x)=(P^{0}x,P^{1}x,P^{2}x,...,P^{n-1}x)^{T}$ ，即

上圖3給出了得到的模式圖示。我們剛剛得到的是一個迴圈矩陣，它具有幾個有趣的特性[34]，[35]。請注意，該模式是確定性的，並且由生成向量 $x$ （第一行）完全指定。而且無論生成向量 $x$ [34]如何，所有迴圈矩陣都通過離散傅立葉變換（DFT）（線性運算）進行對角化。即有

$X=Fdiag(\hat{x})F^{H}$ （7）

其中， $F$ 是一個與向量 $x$ 無關的常數矩陣， $\hat{x}$ 為進行離散傅立葉變換後的向量。（7）式表示了一般迴圈矩陣的特徵分解。共享的、確定性的特徵向量F位於許多不常見特徵的緣由。

對於常數矩陣 $F$ 的表示形式，在迴圈矩陣傅立葉對角化裡面有詳細的推導介紹，該傅立葉矩陣有酉矩陣和對稱矩陣的性質，即 $F^{H}F=I$ ， $F^{H}=F$ 。

4.4 合併

當訓練資料由迴圈移位組成時，我們現在可以應用這一新知識來簡化（3）式中的線性迴歸，由此便使得計算更加簡單。

$\begin{align*} &X^{H}X=Fdiag(\hat{x}^{*})F^{H}Fdiag(\hat{x})F^{H} \\ & = Fdiag(\hat{x}^{*})diag(\hat{x})F^{H} \\ &= Fdiag(\hat {x}^{*} \odot \hat{x})F^{H} \end{align*}$ （10）

其中 $\hat{x}^{*}=(\hat{x})^{H}$ ，由於上式中的第二行為兩個對角矩陣的乘積，即對應對角元素的相應乘積，故用點積符號 $\odot$ 化簡上式。將（10）式代入（3）式（論文附錄A.5推導）：

$\begin{align*} &w=(Fdiag(\hat {x}^{*} \odot \hat{x})F^{H}+\lambda F IF^{H})^{-1}X^{H}y \\ & = (F(diag(\hat {x}^{*} \odot \hat{x})+\lambda I)F^{H})^{-1}X^{H}y \\ &= F(diag(\hat {x}^{*} \odot \hat{x})+\lambda I)^{-1}F^{H}X^{H}y \\ &= Fdiag(\hat {x}^{*} \odot \hat{x}+ \lambda)^{-1}F^{H}F diag(\hat {x}^{*})F^{H}y \\ &= Fdiag(\frac{\hat {x}^{*}}{\hat {x}^{*} \odot \hat{x}+ \lambda})F^{H}y \end{align*}$

對上式左乘常數矩陣 $F$ ，得到：

$\begin{align*} &F^{H}w= F^{H}Fdiag(\frac{\hat {x}^{*}}{\hat {x}^{*} \odot \hat{x}+\lambda})F^{H}y \\ &Fw =diag(\frac{\hat {x}^{*}}{\hat {x}^{*} \odot \hat{x}+\lambda})Fy \\ &\hat {w} =diag(\frac{\hat {x}^{*}}{\hat {x}^{*} \odot \hat{x}+\lambda})\hat {y} \\ &=\frac{\hat {x}^{*}\odot \hat {y}}{\hat {x}^{*} \odot \hat{x}+\lambda} \end{align*}$ （12）

對於計算複雜度，若只考慮脊迴歸，則為 $O(n^{3})$ ；而對於（12）式，其計算複雜度為 $O(nlogn)$ ，若除去最後一步的傅立葉矩陣計算，其複雜度為 $O(n)$ 。

4.5 與相關濾波的聯絡

自80年代以來，相關濾波器一直是訊號處理的一部分，在傅立葉域中解決了無數的目標函式[21]，[28]。最近，他們作為MOSSE濾波器[9]重新出現在人們的視野中，儘管它們簡單且具有處理極快，在跟蹤方面表現出了卓越的效能。

這些過濾器的解決方案看起來像（12）式，但有兩個關鍵的區別：首先，MOSSE濾波器源自在傅立葉域中設計一個特別的目標函式；其次，正則化器 $\lambda$ 以點對點方式新增，以避免被零除。我們在上面展示的推導通過將起始點指定為具有迴圈移位的脊迴歸並且到達相同的結果。

迴圈矩陣豐富了經典訊號處理和現代相關濾波器提出的工具集，並將傅立葉技巧應用於新演算法。在下一節中，我們將在訓練非線性濾波器中看到一個這樣的例項。

5 非線性迴歸

使非線性迴歸函式 $f(z)$ 更強大的的一種方法是使用“核技巧”[23]。最有吸引力的是儘管是在一組不同的變數（在對偶空間）中，此優化問題仍然是線性的。但我們必須注意一點，迴歸函式 $f(z)$ 通常隨著樣本數量的增加而增加。然而，我們用了一種新的分析工具後克服了該限制，並獲得與線性相關濾波器一樣快的非線性濾波器，將其用於訓練和評估。

5.1 核技巧--概述

使用核技巧將線性問題（原空間）的輸入對映到非線性特徵空間（對偶空間） $\varphi (x)$ （基向量）：

1）將向量 $w$ （原空間）表示為對偶空間中基向量的線性組合：

$\dpi{120} w=\sum_{i}\alpha _{i}\Phi (x_{i})$ （13）

此時優化問題轉化為求解向量 $\alpha$ 。

2）定義核函式為向量之間的點積 $\varphi ^{T}(x)\varphi({x}')=k(x,{x}')$ 。

所有樣本對之間的點積通常用 $n\times n$ 維的核矩陣 $K$ 中：

$K_{i,j}=k(x_{i},x_{j})$ （14）

核技巧的特點是採用來自隱式的高維特徵空間 $\varphi (x)$ ，而無需例項化原空間中的向量， $f(z)=w^{T}z= \sum_{i=1}^{n}\alpha _{i}k(z,x_{i})$ （15）。但因為迴歸函式的計算複雜度隨著樣本的數量的增加而增加，為了避免這一問題，我們採用了迴圈矩陣的性質特點。

5.2 快速核迴歸

在文獻8中有對脊迴歸的核心思想：

$\alpha =(K+\lambda I)^{-1}y$ （16）

上式是在對偶空間中的表示方式， $K$ 為核矩陣， $\alpha$ 是由係數 $\alpha _{i}$ 組成的向量。

現在，如果我們可以證明矩陣 $K$ 對於迴圈移位的資料集是迴圈的，對於（16）式，我們可以對矩陣 $K$ 進行對角化，並得到如同線性問題的快速解決方式。任意非線性對映 $\varphi (x)$ 不能保證保留任何型別的結構。但是，我們可以加一個使矩陣 $K$ 迴圈的條件。事實證明它應用相當廣泛，適用於大多數核。

定理1. 對於給定的迴圈資料 $C(x)$ 和任意一個排列矩陣 $M$ ，當核函式滿足 $k(x,{x}')=k(Mx,M{x}')$ 時，相關核矩陣 $K$ 是迴圈矩陣。

證明：（在附錄A.2中給出了證明）

由於核矩陣 $K$ 滿足 $k(x,{x}')=k(Mx,M{x}')$ ，那麼假設矩陣 $K$ 的元素 $K_{i,j}=k(P^{i}x,P^{j}x)$ ，對於任意一個排列矩陣 $M=P^{-i}$ 則有：

$K_{i,j}=k(P^{i}x,P^{j}x)=k(P^{-i}P^{i}x,P^{-i}P^{j}x)=k(x,P^{j-i}x)$ （37）

由於 $P^{n}=P^{0}$ ，故（37）式可改寫為 $K_{i,j}=k(x,P^{(j-i)mod\, n }x)$ （38）

$K= \begin{bmatrix} k(x,P^{0}x) & k(x,P^{1}x) & \cdots & k(x,P^{n-1}x)\\ k(x,P^{1}x) & k(x,P^{2}x) & \cdots & k(x,P^{0}x)\\ \vdots & \vdots & \ddots & \vdots\\ k(x,P^{n-1}x) &k(x,P^{0}x) & \cdots &k(x,P^{n-2}x) \end{bmatrix}$

證畢。

下述的核函式都滿足定理1：

（1）徑向基函式核。例如：高斯核；

（2）點積核。例如：線性核、多項式核；

（3）加權核。例如：交集、 $\chi ^{2}$ 和Hellinger核[36]；

（4）指數加權核。

由於對 $x$ 和 ${x}'$ 的重新排序不會改變它們的 $k(x,{x}')$ ，所以該定理適用於任何維度中的可交換操作組合的任何核運算，例如求和、乘積、取最值。所以我們可以將（16）式作為線性情況對齊公式，用 $K^{xx}$ 表示迴圈矩陣 $K$ 中的第一列向量，則由（7）式可得（在附錄A.3中給出了求解）：

$\begin{align*} \alpha &= (C(k^{xx})+\lambda I)^{-1}y\\ &=(Fdiag(\hat{k}^{xx})F^{H}+\lambda I)^{-1}y \\ &= (Fdiag(\hat{k}^{xx}+\lambda)F^{H})^{-1}y \\ & = Fdiag(\frac{1}{\hat{k}^{xx}+\lambda})F^{H}y \end{align*}$

對公式兩邊進行離散傅立葉變換得： $\hat{ \alpha} = \frac{\hat{y}}{\hat{k}^{xx}+\lambda}$ （17）

作者定義了更通用的核相關，對於兩個任意向量 $x$ 和 ${x}'$ ，它們的核相關向量 $k^{x{x}'}$ 的第 $i$ 個元素為： $k_{i}^{x{x}'}=k({x}',P^{i-1}x)$ （18），換句話說，它表示兩個引數的不同相對位移進行評估的核函式， $\hat{k}^{x{x}}$ 表示在傅立葉域中向量 $x$ 與其自身的核相關性。我們可以將它稱為類似於線性情況的核自相關。對應的，在高維空間 $\varphi (\cdot )$ 中，核函式就用點積表示： $k_{i}^{x{x}'}=\varphi ^{T}({x}')\varphi(P^{i-1}x)$ （19）。可以看出，我們只需要計算和操作核自相關性即可， $k^{x{x}'}$ 是一個 $n\times 1$ 維向量，隨樣本數量呈線性增長，這與核方法的傳統觀點相反，核方法需要計算 $n\times n$ 維的核矩陣，與樣本數量呈平方增長。

由於在逐個檢測設定中無處不在的轉換影象塊，找到最佳的 $\alpha$ 並不是唯一可以加速的方法。在接下來的章節中，我們將研究迴圈移位模型對檢測階段和計算核相關的影響。

5.3 快速檢測

我們很少想要單獨評估一個影象塊的迴歸函式 $f(z)$ 。為了檢測感興趣的目標物件，我們通常希望在幾個影象位置上評估 $f(z)$ ，也就是說這幾個候選塊可以通過迴圈移位來建模。用 $K^{z}$ 表示所有訓練樣本和所有候選塊之間的核矩陣（不對稱）。由於樣本和影象塊分別是基礎樣本 $x$ 和基礎影象塊 $z$ 的迴圈移位組成的，因此矩陣 $K^{z}$ 的每個元素可表示為： $K_{i,j}=k(P^{i-1}z,P^{j-1}x)$ 。很容易驗證該核矩陣滿足定理1，並且對於適當的核函式是迴圈的。

與5.2節類似，我們只需要第一行來定義該核矩陣： $K^{z}=C(k^{xz})$ （20）。由（15）式可知（在附錄A.4中給出了求解），

$\begin{align*} f(z) &= \sum_{i=1}^{n}\alpha _{i}k(z,x_{i})\\ &=(K^{z})^{T}\alpha \\ &= (Fdiag(\hat{k}^{xz})F^{H})^{T}\alpha \\ &= Fdiag(\hat{k}^{xz})F\alpha \end{align*}$

對上式兩邊進行傅立葉變換，得： $\hat{f}(z) = \hat{k}^{xz}\odot \hat{\alpha}$ （22）。可以看出，在所有位置處評估函式 $f(z)$ 可以被視為對核值 $k^{xz}$ 的空間濾波操作。每個評估函式 $f(z)$ 都是來自相鄰核值的 $k^{xz}$ 與學習係數 $\alpha$ 加權的線性組合，因為這是一個濾波操作，因此可以在傅立葉域中更有效地制定

6 快速核相關

儘管我們已經找到了很快的訓練和檢測演算法，但它們仍依賴於計算每個影象塊的核相關性（分別為 $k^{xx}$ 和 $k^{xz}$ ）。回想一下，核相關包括為計算兩個輸入向量所有相對移位的核計算，這是最後一個常見的計算瓶頸，因為對於大小為 $n$ 的訊號，對 $n$ 個核心的簡單評估複雜度為 $O(n^{2})$ ，而使用迴圈移位模型將允許我們在這種昂貴的計算中有效地利用冗餘。

6.1 點積核與多項式核

點積核的形式為 $k(x,{x}')=g(x^{T}{x}')$ ，對於兩個任意向量 $x$ 和 ${x}'$ ，它們的核相關向量 $k^{x{x}'}$ 的第 $i$ 個元素為： $k_{i}^{x{x}'}=k({x}',P^{i-1}x)=g({x}'^{T}P^{i-1}x)$ （23），寫成列向量的形式： $k^{x{x}'}=g(C(x){x}')$ （24），由於 $F(C(x)y)=\hat{x}^{*}\odot \hat{y}$ ，所以對其中的元素進行對角化運算得： $k^{x{x}'}=g(F^{-1}(\hat{x}^{*}\odot {\hat{x}}'))$ （25）

同樣的，對於多項式核 $k(x,{x}')=(x^{T}{x}'+a)^{b}$ ，核向量為 $k^{x{x}'}=(F^{-1}(\hat{x}^{*}\odot {\hat{x}}')+a)^{b}$ （26）

6.2 徑向基函式（RBF）核與高斯核

RBF核的形式為 $k(x,{x}')=h(\left \| x-{x}' \right \|^{2})$ ，與6.1節類似， $k_{i}^{x{x}'}=k({x}',P^{i-1}x)=h(\left \| {x}'-P^{i-1}x \right \| ^{2} )$ （27），由帕斯瓦爾定理【21】得排列矩陣 $P^{i-1}$ 並不影響向量的2-範數，有： $\dpi{120} k_{i}^{x{x}'}=h(\left \| {x}' \right \| ^{2} + \left \| x \right \| ^{2} -2{x}'^{T}P^{i-1}x )$ （28）。可以看出，（28）式與（23）式有相同的點積核形式，故RBF核的列向量形式可寫為： $k^{x{x}'}=h(\left \| {x}' \right \| ^{2} + \left \| x \right \| ^{2} -2F^{-1}(\hat{x}^{*}\odot {\hat{x}}'))$ （29）。

同樣的，作為一個特別有用的特例，對於高斯核 $k(x,{x}')=exp(-\frac{1}{\sigma ^{2}} \left \| x-{x}' \right \|^{2} )$ ，核向量為 $k^{x{x}'}=exp(-\frac{1}{\sigma ^{2}}( \left \| x \right \|^{2} +\left \| {x}' \right \|^{2} -2F^{-1}(\hat{x}^{*}\odot {\hat{x}}') ))$ （30）。和以前一樣，我們可以計算整個核相關性的計算複雜度為 $O(n\, log\, n)$ 。

6.3 其他核

前兩節的方法取決於核矩陣是否由單一變換（例如DFT）保持不變，而這通常不適用於其他核運算，例如交核。我們仍然可以使用快速訓練和檢測的結果（第5.2和5.3節），但必須通過更昂貴的滑動視窗方法來評估核相關性。

7 多通道核變換

在本節中，我們將看到在對偶空間中具有允許多個通道（例如HOG描述符[20]的方向區間）的優點，只需在傅立葉域中對它們求和即可。該特徵延伸到線性情況，在特定情況下顯著簡化了最近提出的多通道相關濾波器[31]，[32]，[33]。

7.1 一般情況

在本節中我們針對多通道假設向量 $x$ 是連線 $C$ 個通道每個通道中的各個向量（例如，HOG變體的31個梯度方向區[20]），如 $x=[x_{1},\cdots ,x_{C}]$ 。請注意，第6節中研究的所有核函式都基於引數的點積等運算，可以通過簡單地對每個通道的各個點積進行求和來進行計算。 由於離散傅立葉變換的線性性質，對傅立葉域中每個通道的結果求和即可。 作為一個具體的例子，我們可以將這個推理應用於高斯核，得到（30）式的多通道模擬：

$k^{x{x}'}=exp(-\frac{1}{\sigma ^{2}}( \left \| x \right \|^{2} +\left \| {x}' \right \|^{2} -2F^{-1} (\sum_{C}\hat{x}_{C}^{*}\odot {\hat{x}_{C}}') ))$ （31）

可以看出，多個通道的整合不會導致更難的推理問題 --- 我們只需在計算核相關函式時對通道求和即可。

7.2 線性核

對於最簡單的線性核 $k(x,{x}')=x^{T}{x}'$ ，對於擴充套件後的多通道為： $k^{x{x}'}=2F^{-1} \sum_{C}(\hat{x}_{C}^{*}\odot {\hat{x}_{C}}')$ （32），我們將其稱之為對偶相關濾波（DCF），該濾波為線性濾波，但它是在對偶空間 $\alpha$ 中進行的訓練，接下來將會提到其他多通道濾波器的優勢。

線性相關濾波器擴充套件到多個通道由這三組獨立發現[31]，[32]，[33]。在脊迴歸的情況下，通過將問題分解為對每個DFT頻率組建一個線性系統，使得它們在訓練的速度方面比非結構化演算法更快。 Henriques等[31]另外將其推廣到其他訓練演算法。但是，（32）式表明，在帶有線性核的對偶空間中訓練一個具有多個通道的線性分類器，僅使用逐元素進行運算。這可能是一開始就不太理想，因為這需要更昂貴的矩陣求逆[31] ，[32]，[33]。

我們通過如下方法來解決這種差異：我們只考慮單個基礎樣本向量 $x$ ，在這種情況下，無論特徵或通道的數量如何，核矩陣 $K=XX^{T}$ 都是 $n\times n$ 維的，它涉及基礎樣本 $x$ 的 $n$ 個迴圈移位，並且可以通過DFT對其對角化（（10）式可知），由於 $K$ 是完全對角的，故我們可以單獨使用元素操作。但對於兩個基礎樣本向量，則 $K$ 變為 $2n\times 2n$ 並且離散傅立葉變換不再足以完全對角化核矩陣 $K$ ，這種不完全對角化（塊對角化）需要更昂貴的操作來處理，這些皆在本論文中提出。

一個有趣的對稱論證：在原始空間中使用多個基本樣本和單個通道進行訓練，並只進行逐元素操作（附錄A.6）。接下來，將相同的推理應用於非中心協方差矩陣 $X^{T}X$ ，而不是 $XX^{T}$ 。在這種情況下，我們獲得了原始的MOSSE過濾器[9]。

總之，對於快速逐元素操作，我們可以選擇多個通道（通過在對偶空間中進行離散傅立葉變換）或多個基本樣本（通過在原始空間中進行MOSSE操作），但不能都選擇。這對時間敏感型模型（如跟蹤）具有重要影響。一般情況[31]更昂貴，其主要適用於離線訓練。

8 實驗結果

8.1 跟蹤管道

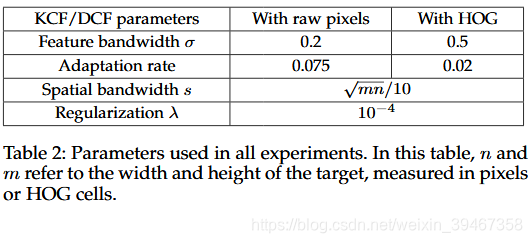
我們在Matlab中實現了兩個簡單的跟蹤器，它們基於所提出的高斯核相關濾波器（KCF），對偶線性核相關濾波器（DCF）。我們在這裡不展示多項式核的效果，因為它們與高斯核的效果相同，並且需要更多的引數。我們還測試了另外兩個變體：一個直接作用於原始畫素值，另一個為影象塊是4畫素，特別是Felzenszwalb的變體[20]，[22]的HOG描述符。注意，在單個通道（原始畫素）的限制情況下，我們的線性DCF等同於MOSSE [9]，並且它還具有支援多個通道（例如HOG）的優點。 我們的跟蹤器只需要很少的引數，我們會在表2中報告我們使用的引數，這些值是針對所有視訊修復的。

表2：所有實驗中使用的引數。在此表中，n和m指的是目標的寬度和高度，以畫素或HOG單元格為單位

KCF的大部分功能在演算法1中表示為Matlab程式碼。與此工作的早期版本[29]不同，該工作處理了多通道，其可以在輸入陣列的第三個維度中可以看出。它實現了3個函式：訓練（17）式，檢測（22）式和用到前二者函式的多通道核相關（31）式。

跟蹤器的管道很簡單，並且不包括用於故障檢測或運動建模的任何啟發式。在第一幀中，我們訓練模型，其中影象塊位於目標的初始位置。此影象塊大於目標，以提供一些上下文。對於每個新目標幀，我們檢測前一個位置的影象塊，並將目標位置更新為產生最大值的位置。最後，我們在新位置訓練一個新模型，並將得到的 $\alpha$

KCF(High-Speed Tracking with Kernelized Correlation Filters)論文詳解

摘要