《程式設計師的演算法趣題》-(日)增井敏克 ， 書中為69 道數學謎題編寫了解題程式， 程式語言為：Ruby，JavaScript，C語言。有興趣的同學，可以購書閱讀~

在此更新個人編寫的Python版，僅供學習使用。（執行環境：Python3.6）

Q15 走樓梯

    A上樓梯時， B 從同一樓梯往下走。每次不一定只走 1 級，最多可以一次跳過 3 級（即直接前進 4 級）。但無論走多少級， 1 次移動所需時間不變。兩人同時開始走，求共有多少種“兩人最終同時停在同一級”的情況（假設樓梯寬度足夠，可以相互錯開，不會撞上。另外，同時到達同一級時視為結束）。
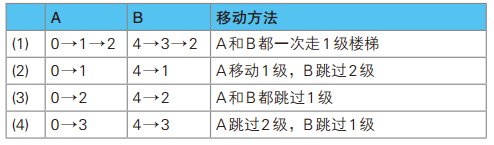
    舉個例子，有 4 級樓梯的時候，結果如表所示，共有 4 種情況（假設每級樓梯上寫著 0~4 這幾個數字）。

                                 

問題
    求當存在 10 級樓梯，且移動規則相同時，有多少種兩人最終同時停在同一級的情況？

max_steps = 4

meet_count = 0
def walk(a_pos, b_pos):
    for a_step in range(1, max_steps+1):
        a_next_pos = a_pos+a_step
        for b_step in range(1, max_steps+1):
            b_next_pos = b_pos-b_step
            if a_next_pos == b_next_pos:
                global meet_count
                meet_count += 1
            elif a_next_pos < b_next_pos:
                walk(a_next_pos, b_next_pos)
            else:
                continue

walk(0, 10)
print("有%s種" % meet_count)
 

執行結果：

                 有201種