《程式設計師的演算法趣題》-(日)增井敏克 ， 書中為69 道數學謎題編寫了解題程式， 程式語言為：Ruby，JavaScript，C語言。有興趣的同學，可以購書閱讀~

在此更新個人編寫的Python版，僅供學習使用。（執行環境：Python3.6）

Q10 輪盤的最大值

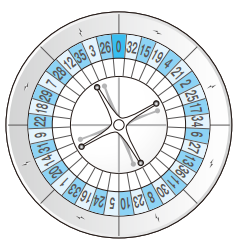
      流傳較廣的輪盤數字排布和設計有“歐式規則”和“美式規則”兩種。下面我們要找出在這些規則下，“連續 n 個數字的和”最大的位置。

      舉個例子，當 n ＝ 3 時，按照歐式規則得到的和最大的組合是 36,11, 30 這個組合，和為 77；而美式規則下則是 24, 36, 13 這個組合，得到的和為73。

                                                                 

                                                                                  歐式規則

歐式規則
        0, 32, 15, 19, 4, 21, 2, 25, 17, 34, 6, 27, 13, 36, 11, 30, 8, 23, 10, 5, 24, 16, 33, 1, 20, 14, 31, 9, 22, 18, 29, 7, 28, 12, 35, 3, 26
美式規則
       0, 28, 9, 26, 30, 11, 7, 20, 32, 17, 5, 22, 34, 15, 3, 24, 36, 13, 1, 00, 27, 10, 25, 29, 12, 8, 19, 31, 18, 6, 21, 33, 16, 4, 23, 35, 14, 2

問題
      當 2 ≤ n ≤ 36 時，求連續 n 個數之和最大的情況，並找出滿足條件"歐式規則下的和小於美式規則下的和"的 n 的個數。

import time

european = [0, 32, 15, 19, 4, 21, 2, 25, 17, 34, 6, 27, 13, 36, 11, 30, 8, 23, 10, 5, 24, 16, 33, 1, 20, 14, 31, 9, 22,
            18, 29, 7, 28, 12, 35, 3, 26]
american = [0, 28, 9, 26, 30, 11, 7, 20, 32, 17, 5, 22, 34, 15, 3, 24, 36, 13, 1, 00, 27, 10, 25, 29, 12, 8, 19, 31,
            18, 6, 21, 33, 16, 4, 23, 35, 14, 2]

# 常規演算法
def max_sum(cal_list, n):
    res_max = 0
    for start_pos in range(len(cal_list)):
        if start_pos+n > len(cal_list):
            n_list = cal_list[start_pos:]
            n_list += cal_list[:start_pos+n-len(cal_list)]
        else:
            n_list = cal_list[start_pos:start_pos+n]
        n_sum = sum(n_list)
        if n_sum > res_max:
            res_max = n_sum
    return res_max

# 蠕蟲演算法
def worm_sum(cal_list, n):
    res_max = cal_sum = sum(cal_list[:n])
    for start_pos in range(0, len(cal_list)):
        end_pos = (start_pos + n) % len(cal_list)
        cal_sum = cal_sum - cal_list[start_pos] + cal_list[end_pos]
        if cal_sum > res_max:
            res_max = cal_sum
    return res_max

def calc_result(use_method):
    start_time = time.time()
    result_number = 0
    for n in range(2, 37):
        european_max = use_method(european, n)
        american_max = use_method(american, n)
        if european_max < american_max:
            result_number += 1

    print("滿足條件的n的個數為：%s, (耗時 %0.5f s)" % (result_number, time.time()-start_time))

calc_result(max_sum)
calc_result(worm_sum)

執行結果：

            滿足條件的n的個數為：9, (耗時 0.00398 s)
           滿足條件的n的個數為：9, (耗時 0.00101 s)