前言

本篇文章來自Artificial Intelligence: A Modern Approach一書第17章“複雜決策問題”，進行了翻譯和整理，僅供學習參考。

正文

在之前的章節中討論了單個決策問題，這些問題特點是行動帶來的效用是完全知道的，而接下來討論的序貫決策問題，效用取決於一序列的行動，而不是單個的行動。舉個例子，就像下象棋一樣，最後的輸贏並不能夠從一開始下的幾步就可以預見到，只有當你最後輸了或者贏了的時候，再回過頭去分析自己走過的每一步，就會發現有哪幾步走得不好，影響了後面幾步，乃至決定了勝負。但是在下棋過程，你是不知道，也無法確定那幾步就會決定勝負關係的。所以說下象棋的輸贏取決於一系列的步數，而不是單個的下子。

17.1 序貫決策問題

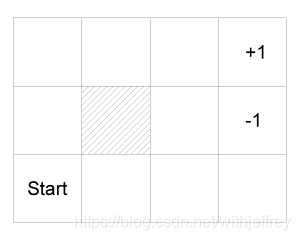
現在設定一個如上圖所示的遊戲，規則是智慧體從Start位置開始，每步只能按照上下左右的動作走一格，當到達+1和-1時遊戲結束，當智慧體到達+1則表示贏得了遊戲。如果智慧體選擇其中一種動作，而且該動作100%會執行或者說發生，那麼很明顯可以按照上上右右右或者右右上上上的順序依次執行，達到+1。但是如果這是一個充滿著“不確定”的世界，當智慧體選擇某一種動作時，只有80%的概率到達動作期望的狀態，而20%的概率則是與所選擇動作呈90°的方向到達另一個狀態。比如說，從（1，1）開始，如果選擇上，並且最終到達狀態（1，2）的概率只有80%，而實際執行右併到達（2，1）有10%概率，實際執行左將碰到牆壁而保持不動有10%概率。我們用轉換模型（Transition Model）來表示這樣一組從一個狀態因採取不同的動作到達另一個狀態的概率模型。

現在我們來定義效用函式。定義一個動作序列的效用函式就是最後狀態的效用減去0.04*動作序列的長度，也就是說，每一個除了+1和-1的狀態，都有-0.04的“獎勵”，而一系列的狀態的獎勵之和可以計算出其效用。比如說動作序列長度為6，那麼一系列動作後到達+1，那麼效用為0.76。在一個“確定”的世界，智慧體在給定的動作下可以到達期望的狀態，而在一個“不確定”的世界，智慧體雖然給定了動作，但是有一定的概率達到期望的狀態。比如說，智慧體在（3，2），動作是（上，右），那麼它到達（4，3）狀態的概率是0.64。具體過程如下圖所示：

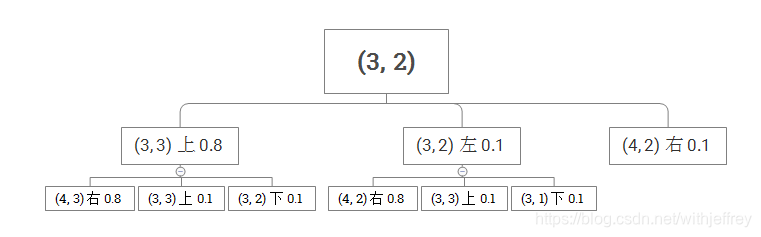
它可能到達的狀態有5個：

• 到達（4，3）的概率為0.8*0.8=0.64
• 到達（3，3）的概率為0.8*0.1+0.1*0.1=0.09
• 到達（3，2）的概率為0.8*0.1=0.08
• 到達（4，2）的概率為0.1*0.8+0.1=0.18
• 到達（3，1）的概率為0.1*0.1=0.01

正好所有的概率之和為0.64+0.09+0.08+0.18+0.01=1

一個完整的從狀態到動作的對映稱之為策略。給定一個策略，可以計算出該策略的期望效用。所以，我們要解決的問題也就是計算出最佳的策略，即可以最大化期望效用的策略。這樣一個理想和隨機的世界，通過轉換模型尋找最佳策略的問題稱之為馬可夫決策問題（MDP），以俄羅斯的統計學家Andrei A. Markov命名。馬可夫屬性是指任何一個狀態的轉換概率僅僅取決於當前該狀態，而與之前的歷史狀態無關。

另外，如果是在一個非理想的環境中，智慧體在感知時不能獲取到足夠的資訊來描述其當前的狀態以及轉換概率。在運籌學領域，這樣的問題被稱為部分可觀測馬可夫決策問題（POMDP）。這一點暫時不展開。

17.2 值迭代

通過值迭代的演算法來計算最佳策略。值迭代的基本思路是先計算每個狀態的效用U(state)，然後根據效用選擇每個狀態的最佳行動。
首先需要定義每個狀態的效用函式：
$R(i) = EU(H(i, policy*|M) = \sum P(H(i, policy*)|M)U_h(H(i, policy*)) \quad (17.1)$

這裡的policy*是由轉換模型M和序列U_h的效用決定的。這裡的U_h要求符合可分割特性，該特性表明可以找到一個函式f使得U_h滿足：
$U_h([s_0, s_1, ..., s_n]) = f(s_0, U_h([s_1, ..., s_n]))$
最簡單的函式是加法：
$U_h([s_0, s_1, ..., s_n]) = R(s_0) + U_h([s1, ..., s_n]))$
這裡的R是獎勵函式。
給定Uh，可以進一步得到：
$policy^*(i) = \mathop {argmax}_{a} \sum_{j} M_{ij}^{a}U(j) \quad (17.2)$
$U(i) = R(i) + \mathop {max}_{a} \sum_{j} M_{ij}^{a} U(j) \quad (17.3)$
公式(17.3)是動態程式設計的基礎，是解決序貫決策問題的一種解，由1950年末Richard Bellman發現。
反覆地使用公式(17.3)，每一步都使用鄰近狀態的舊的效用估計值來更新狀態的效用，可以得到下面的公式：
$U_{t+1} (i) \leftarrow R(i) + \mathop {max}_{a} \sum_j M_{ij}^{a} U_{t} (j) \quad (17.4)$
其中Ut(i)是在迭代t次後在狀態i的效用估計值。隨著t->∞，效用會收斂於一個穩定的值。這樣一個演算法稱之為值迭代。

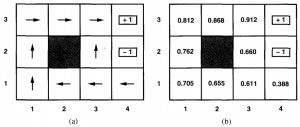
使用值迭代演算法來計算在17.1一節介紹的遊戲，那麼它的最佳策略和狀態效用為：

17.3 策略迭代
策略迭代演算法是選擇一個初始策略，然後計算在該策略下每一個狀態的效用。然後通過下一個狀態的效用來更新在每一個狀態下的策略，直到策略達到穩定。在給定策略下決定效用的步驟被稱之為value determination。

value determination演算法可以通過以下兩種方法表述：
第一種是簡化版的值迭代，如下所示：
$U_{t+1} (i) \leftarrow R(i) + \sum_{j} M_{ij}^{Policy(i)} U_{t} (j)$
以及從策略迭代中獲取的當前效用估計值作為初值值。

第二種是直接求解效用。給定策略P，狀態的效用遵從以下一組等式：
$U(i) = R(i) + \sum_{j} M_{ij}^{P(i)} U_{t} (j)$
舉個例子，假設P就是17.1提到的遊戲的最佳策略，那麼根據轉換模型M，可以得到下面的等式：
$u_{(1,1)} = 0.8u_{(1,2)}+0.1u_{(1,1)}+0.1u_{(2,1)}$