實驗題目：寫一Sherwood演算法C，與演算法A, B, D比較，給出實驗結果

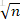
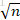
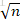
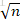
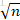
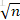
演算法的思想很簡單，因為經過計算，演算法B是從val前個數中找到一個不大於x的數y，然後從y開始尋找，直到找到x返回x的下標。那麼作為一個概率演算法，演算法C採用與B相似的思維，只不過演算法C不是直接從val前個數中找，而是隨機產生個數，接下來做與演算法B相同工作，就是找這數中不大於x的最大的數，然後再從這個數開始search。因為val作為一個完全隨機的陣列，隨機選取個數和選取前個數效果是一樣的。

這裡給出演算法A、B、C、D程式碼。

// HomeWork_P67.cpp : 此檔案包含 "main" 函式。程式執行將在此處開始並結束。
//

#include "pch.h"
#include <iostream>
#include <random>
#include <vector>
#include <ctime>
#include <algorithm>
#include<fstream>
#define MAXN 10000
using namespace std;
//產生一個隨機陣列val
vector<int> getVector() {

	vector<int> val(1000);
	for (auto i = 0; i < val.size(); ++i)
		val[i] = i;
	uniform_int_distribution<unsigned> u(0, 999);
	default_random_engine e(time(0));
	for (auto i = 0; i < val.size(); ++i)
	{
		int tmpa = u(e);
		int tmpb = u(e);
		swap(val[tmpa], val[tmpb]);
	}
	return val;

}
//列印陣列
void print(vector<int> v) {
	for (auto i : v)
		cout << i << " ";
	cout << endl;
}
//生成陣列ptr[]
vector<int> getPtr(vector<int> val) {
	//演算法思想：每次選出val的最小值，將其標記為MAXN，那麼下一個最小值就是當前值的next。當前的ptr值就應該是下一個的下標
	vector<int> ptr(val.size(),-1);
	auto min_it = min_element(val.begin(), val.end());
	int pos = min_it-val.begin();
	int head = pos;
	while (*min_it != MAXN) {
		*min_it = MAXN;
		
		pos = min_it - val.begin();
		
		min_it = min_element(val.begin(), val.end());

		ptr[pos] = min_it - val.begin();
		
	}
	ptr[pos] = head;
	return ptr;
}
//查詢x在陣列val的下標.返回pair(下標，比較次數)
pair<int,int> Search(int x, int i,vector<int> val,vector<int> ptr) {
	int count = 1;//統計比較次數
	while (x > val[i]) {
		i = ptr[i];
		++count;
	}
	return { i,count };
}
//確定性演算法A(x)，在表val中查詢x的下標
pair<int, int> A(int x, vector<int> val, vector<int> ptr) {
	int head = min_element(val.begin(), val.end()) - val.begin();
	return Search(x, head, val, ptr);
}
//概率演算法D(x)，在表val中查詢x的下標
pair<int, int> D(int x, vector<int> val, vector<int> ptr) {
	default_random_engine e(time(0));
	uniform_int_distribution<int> u(0, val.size());
	int head = min_element(val.begin(), val.end()) - val.begin();
	int i = u(e);
	int y = val[i];
	if (x < y)
		return Search(x, head, val, ptr);
	else if (x > y)
		return Search(x, ptr[i], val, ptr);
	else
		return { i ,0};
}
//確定性演算法B(x)，在表val中查詢x的下標
pair<int, int> B(int x, vector<int> val, vector<int> ptr) {
	int head = min_element(val.begin(), val.end()) - val.begin();
	int max = val[head];
	int i = head;
	int y = -1;
	for (int j = 0; j < sqrt(val.size()); ++j) {
		y = val[j];
		if (max < y&&y <= x) {
			i = j;
			max = y;
		}
	}
	return Search(x, i,val,ptr);
}
//概率演算法C(x),先隨機取L個下標，找到一個不大於x的數，從這個數開始查詢。
pair<int, int> C(int x, vector<int> val, vector<int> ptr) {
	int L = sqrt(val.size());
	uniform_int_distribution<int> u(0, 999);
	default_random_engine e(time(0));
	vector<int> xb;
	for (auto i = 0; i < L; ++i)
		xb.push_back(u(e));
	int i = xb[0];
	int y = -1;
	int max = i;
	for (int j = 0; j < L; ++j) {
		y = val[xb[j]];
		if (max < y&&y < x) {
			i = xb[j];
			max = y;
		}
	}
	return Search(x, i, val, ptr);
}

//測試向檔案輸入資料 用於測試陣列
void fwrite(vector<int> v) {
	ofstream os("a.txt");
	
	for (auto i = 0; i < v.size(); ++i) {
		os << v[i] << " ";
		if ((i+1) % 10 == 0)
			os << endl;
	}

}
//測試隨機陣列 從檔案中讀取val
vector<int> getVal() {
	vector<int> val;
	ifstream is("a.txt");
	int tmp;
	while (is >> tmp)
		val.push_back(tmp);
	return val;
}
//隨機抽10個數字，
vector<int> randVal() {
	uniform_int_distribution<int> u(0, 999);
	default_random_engine e(time(0));
	vector<int> rV;
	for (auto i = 0; i < 100; ++i)
		rV.push_back(u(e));
	return rV;
}
//各演算法查詢10個隨機數，的查詢次數
int searchTime(pair<int, int>(*pf)(int , vector<int> , vector<int> ), vector<int> val,vector<int> ptr,vector<int> RV) {
	int sum = 0;//統計總共比較次數
	for (auto si : RV) {
		pair<int, int> p = pf(si, val, ptr);
		sum += p.second;
	}
	return 1.0*sum / RV.size();

}
int main() {
	
	vector<int> val = getVector();
	vector<int> ptr = getPtr(val);
	//隨機抽100個數字，測試他們用四種方法所需要查詢的次數
	vector<int> RV = randVal();
	cout << "隨機抽100個數字如下：\n";
	for (auto i : RV)
		cout << i << " ";
	cout << endl;

	//用演算法
	cout <<"演算法A 查詢這100個數字的平均查詢次數	" << searchTime(A,val,ptr,RV) <<endl;
	cout << "演算法B 查詢這100個數字的平均查詢次數	" << searchTime(B, val, ptr, RV) << endl;
	cout << "演算法C 查詢這100個數字的平均查詢次數	" << searchTime(C, val, ptr, RV) << endl;
	cout << "演算法D 查詢這100個數字的平均查詢次數	" << searchTime(D, val, ptr, RV) << endl;
	
}