一直以來都以為自己對一些演算法已經理解了，直到最近才發現，梯度下降都理解的不好。

1 問題的引出

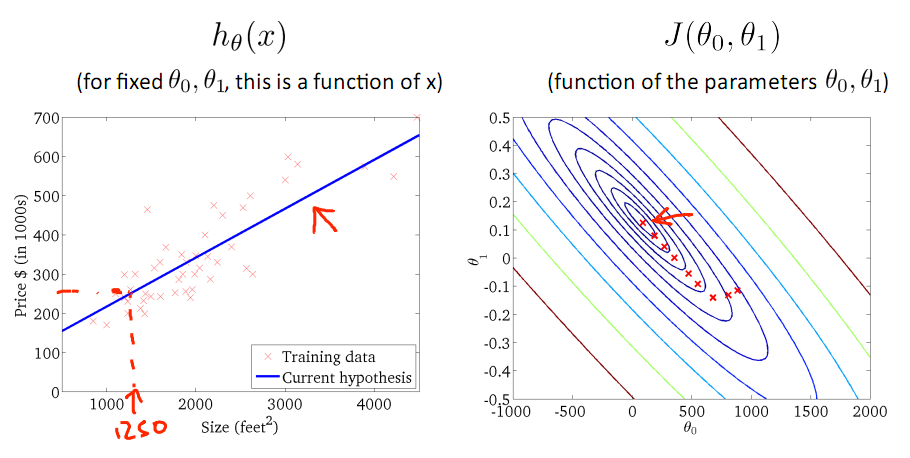
對於上篇中講到的線性迴歸，先化一個為一個特徵θ1，θ0為偏置項，最後列出的誤差函式如下圖所示：

手動求解

目標是優化J(θ1)，得到其最小化，下圖中的×為y(i)，下面給出TrainSet，{(1,1),(2,2),(3,3)}通過手動尋找來找到最優解，由圖可見當θ1取1時，與y(i)完全重合，J(θ1) = 0

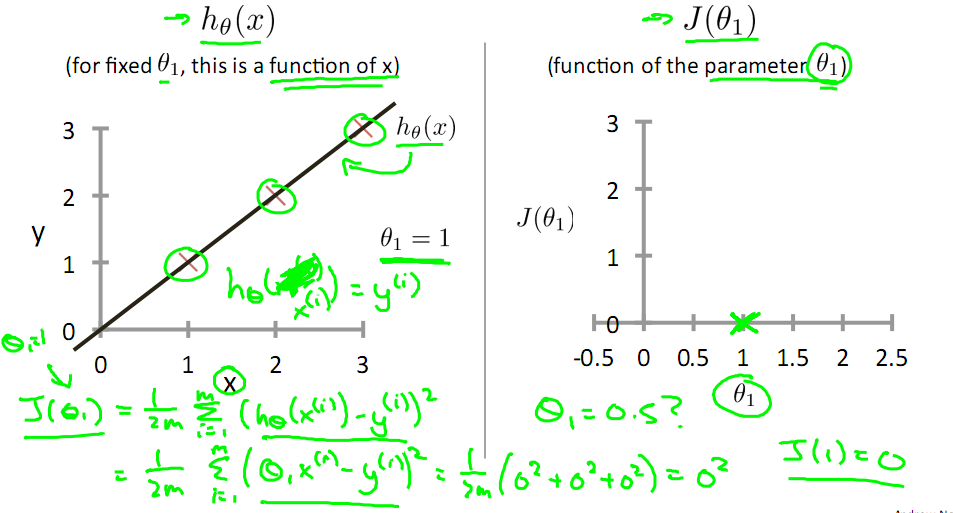
下面是θ1的取值與對應的J(θ1)變化情況

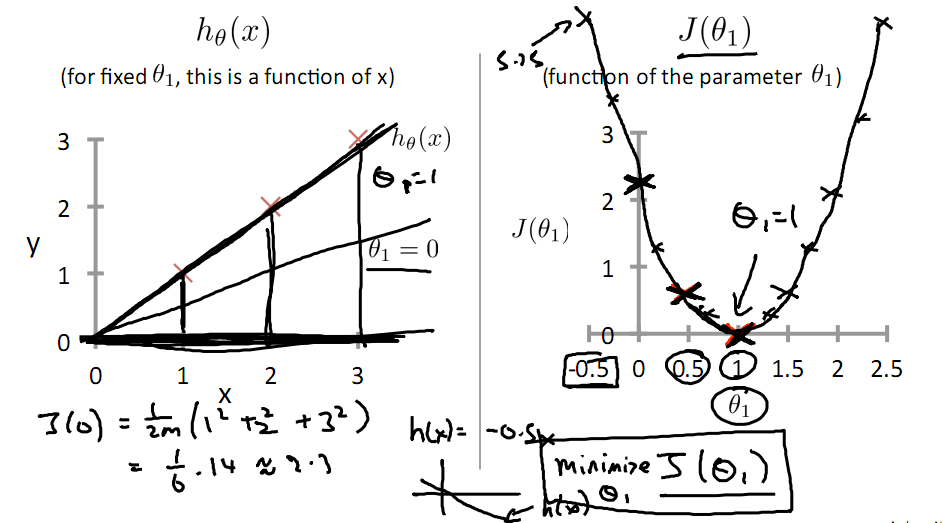
由此可見，最優解即為0，現在來看通過梯度下降法來自動找到最優解，對於上述待優化問題，下圖給出其三維影象，可見要找到最優解，就要不斷向下探索，使得J(θ)最小即可。

2 梯度下降的幾何形式

下圖為梯度下降的目的，找到J（θ）的最小值。

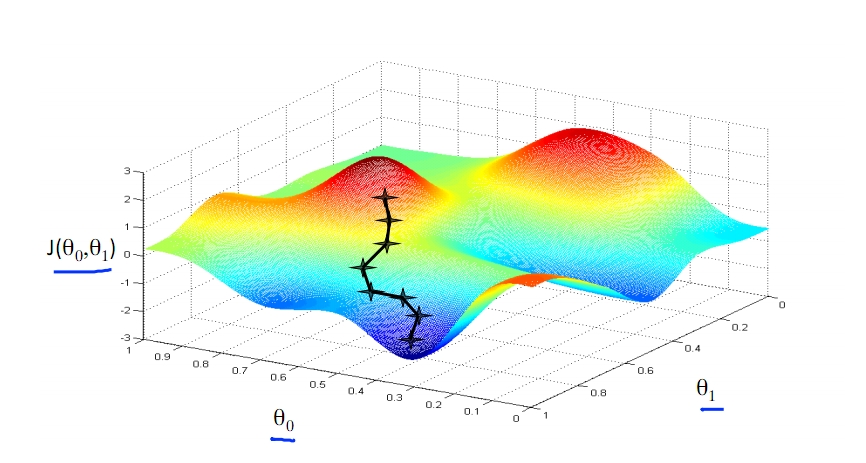
其實，J(θ)的真正圖形是類似下面這樣的，因為其是一個凸函式，只有一個全域性最優解，所以不必擔心像上圖一樣找到區域性最優解

直到了要找到圖形中的最小值之後，下面介紹自動求解最小值的辦法，這就是梯度下降法

對引數向量θ中的每個分量θj，迭代減去速率因子a* (dJ(θ)/dθj)即可，後邊一項為J(θ)關於θj的偏導數

3 梯度下降的原理

導數的概念

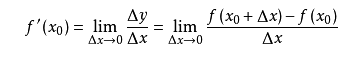
由公式可見，對點x0的導數反映了函式在點x0處的瞬時變化速率，或者叫在點x0處的斜度。推廣到多維函式中，就有了梯度的概念，梯度是一個向量組合，反映了多維圖形中變化速率最快的方向。

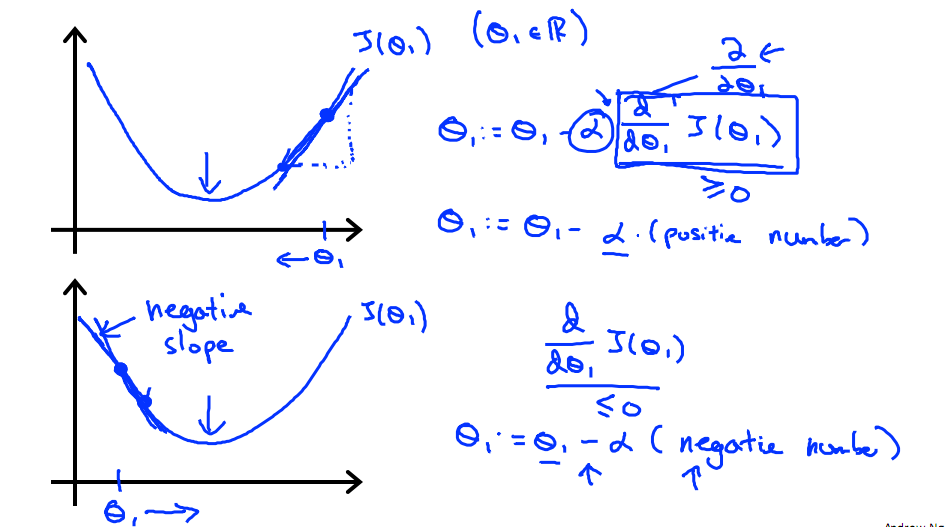
下圖展示了對單個特徵θ1的直觀圖形，起始時導數為正，θ1減小後並以新的θ1為基點重新求導，一直迭代就會找到最小的θ1，若導數為負時，θ1的就會不斷增到，直到找到使損失函式最小的值。

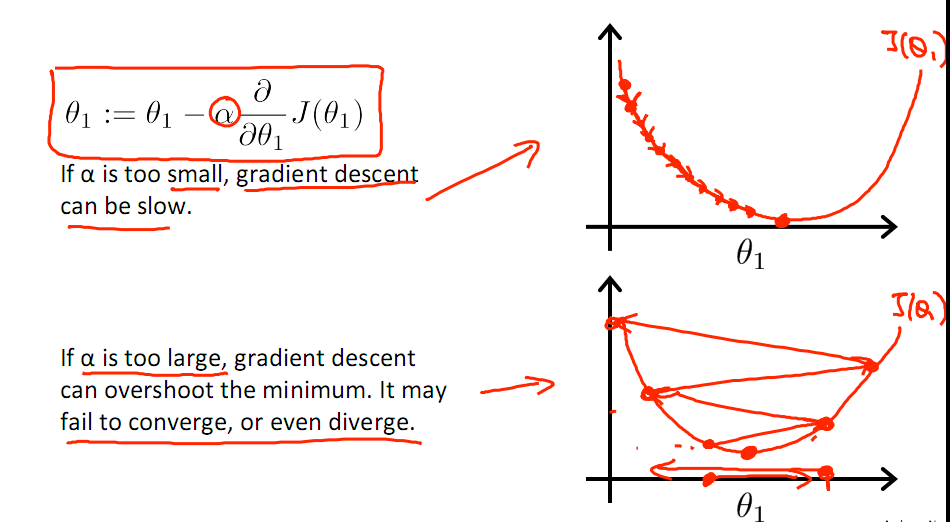
有一點需要注意的是步長a的大小，如果a太小，則會迭代很多次才找到最優解，若a太大，可能跳過最優，從而找不到最優解。

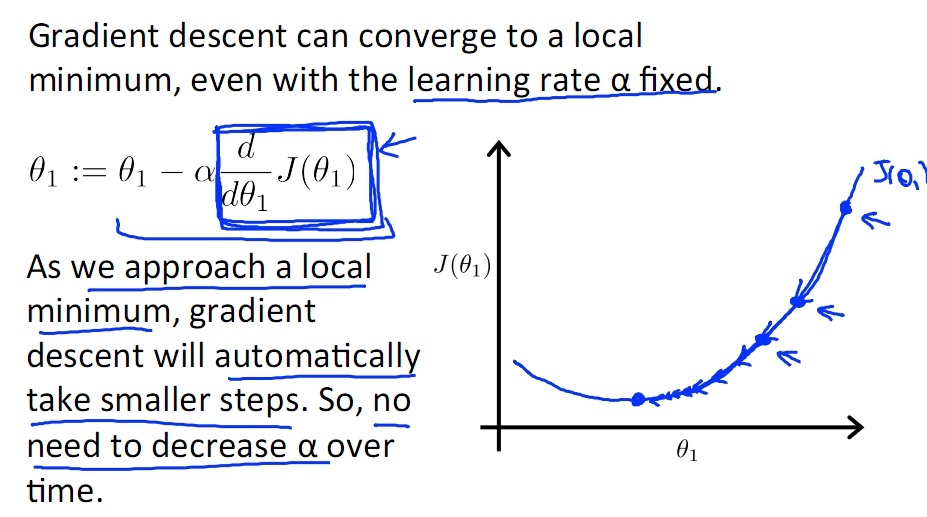
另外，在不斷迭代的過程中，梯度值會不斷變小，所以θ1的變化速度也會越來越慢，所以不需要使速率a的值越來越小

下圖就是尋找過程

當梯度下降到一定數值後，每次迭代的變化很小，這時可以設定一個閾值，只要變化小魚該閾值，就停止迭代，而得到的結果也近似於最優解。

若損失函式的值不斷變大，則有可能是步長速率a太大，導致演算法不收斂，這時可適當調整a值

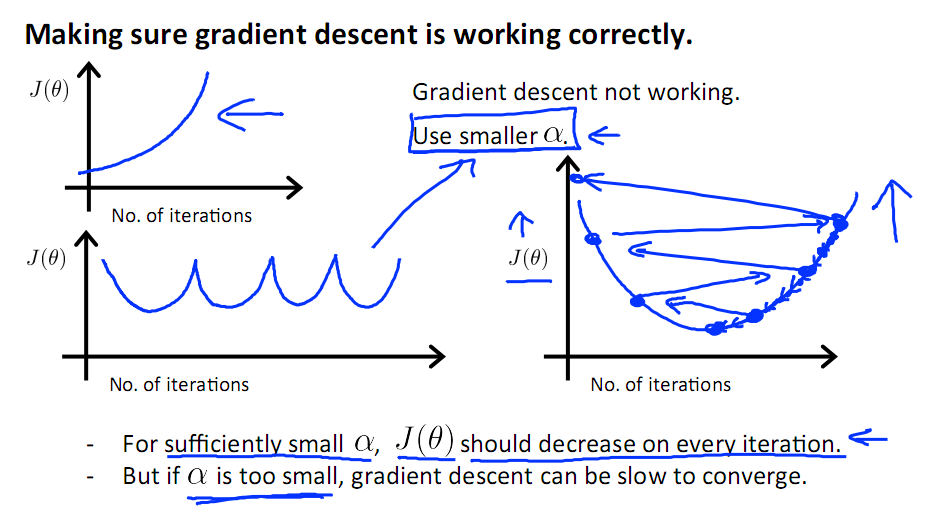
為了選擇引數a，就需要不斷測試，因為a太大太小都不太好。

如果想跳過的a與演算法複雜的迭代，可以選擇 Normal Equation。

4 隨機梯度下降

對於樣本數量額非常之多的情況，Batch Gradient Descent演算法會非常耗時，因為每次迭代都要便利所有樣本，可選用Stochastic Gradient Descent 演算法，需要注意外層迴圈Loop，因為只遍歷一次樣本，不見得會收斂。

隨機梯度演算法就可以用作線上學習了，但是注意隨機梯度的結果並非完全收斂，而是在收斂結果處波動的，可能由非線性可分的樣本引起來的：

可以有如下解決辦法：（來自MLIA）

1. 動態更改學習速率a的大小，可以增大或者減小

2. 隨機選樣本進行學習