numpy常用函式2
numpy常用函式學習2
目錄
點乘法
該方法為數學方法,但是在numpy使用的時候略坑。numpy的點乘為a.dot(b)或numpy.dot(a,b),要求a,b的原始資料結構為MxN .* NxL=MxL,不是顯示資料,必須經過a.resize()或者a.shape=兩種方法轉換才能將原始資料改變結構。
程式碼如下:
>>> 線型預測
通過最小二乘法對已有資料擬合出函式,並預測未知資料。
最小二乘法:在假定函式結構(這裡假設我們知道結果是y=ax+b)的情況下,通過已知結果(x,y)求取未知變數(a,b)。
具體求取原理參考:https://baijiahao.baidu.com/s?id=1613474944612061421&wfr=spider&for=pc
預測例子:
import datetime as dt
import numpy as np
import pandas as pd
import matplotlib.pyplot as mp
import matplotlib.dates as md
def dmy2ymd(dmy):
dmy = str(dmy, encoding='utf-8')
date = dt.datetime.strptime(dmy, '%d-%m-%Y').date()
ymd = date.strftime('%Y-%m-%d')
return ymd
dates, closing_prices = np.loadtxt(
'../../data/aapl.csv', delimiter=',',
usecols=(1, 6), unpack=True,
dtype='M8[D], f8', converters={1: dmy2ymd})
N = 5
pred_prices = np.zeros(
closing_prices.size - 2 * N + 1)
for i in range(pred_prices.size):
a = np.zeros((N, N))
for j in range(N):
a[j, ] = closing_prices[i + j:i + j + N]
b = closing_prices[i + N:i + N * 2]
#[1]擠後面的為殘差
x = np.linalg.lstsq(a, b)[0]
pred_prices[i] = b.dot(x)
mp.figure('Linear Prediction',
facecolor='lightgray')
mp.title('Linear Prediction', fontsize=20)
mp.xlabel('Date', fontsize=14)
mp.ylabel('Price', fontsize=14)
ax = mp.gca()
# 設定水平座標每個星期一為主刻度
ax.xaxis.set_major_locator(md.WeekdayLocator(
byweekday=md.MO))
# 設定水平座標每一天為次刻度
ax.xaxis.set_minor_locator(md.DayLocator())
# 設定水平座標主刻度標籤格式
ax.xaxis.set_major_formatter(md.DateFormatter(
'%d %b %Y'))
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
dates = dates.astype(md.datetime.datetime)
mp.plot(dates, closing_prices, 'o-', c='lightgray',
label='Closing Price')
dates = np.append(dates,
dates[-1] + pd.tseries.offsets.BDay())
mp.plot(dates[2 * N:], pred_prices, 'o-',
c='orangered', linewidth=3,
label='Predicted Price')
mp.legend()
mp.gcf().autofmt_xdate()
mp.show()
線性擬合
原理同上:通過最小二乘法對已有資料擬合出函式,並預測未知資料。
y`代表預測值
y-y`為誤差
kx + b = y y`
kx1 + b = y1 y1` (y1-y1`)^2
kx2 + b = y2 y2` (y2-y2`)^2
...
kxn + b = yn yn` (yn-yn`)^2
----------------------------------------------------------
E=f(,k,b)
找到合適的k和b,使E取得最小,由此,k和b所確定的直線為擬合直線。
/ x1 1 \ / k \ / y1` \
| x2 1 | X | b | 接近 | y2` |
| ... | \ / | ... |
\ xn 1/ \ yn`/
a x b
最小二乘法的方法:
= np.linalg.lstsq(a, b)[0]
y = kx + b
kx1 + b = y1' - y1
kx2 + b = y2' - y2
...
kxn + b = yn' - yn
[y1 - (kx1 + b)]^2 +
[y2 - (kx2 + b)]^2 + ... +
[yn - (kxn + b)]^2 = loss = f(k, b)
k, b? -> loss ->min
趨勢線示例:
# -*- coding: utf-8 -*-
from __future__ import unicode_literals
import datetime as dt
import numpy as np
import matplotlib.pyplot as mp
import matplotlib.dates as md
def dmy2ymd(dmy):
dmy = str(dmy, encoding='utf-8')
date = dt.datetime.strptime(dmy, '%d-%m-%Y').date()
ymd = date.strftime('%Y-%m-%d')
return ymd
dates, opening_prices, highest_prices, \
lowest_prices, closing_prices = np.loadtxt(
r'C:\Users\Cs\Desktop\資料分析\DS+ML\DS\data\aapl.csv',
delimiter=',', usecols=(1, 3, 4, 5, 6),
unpack=True, dtype='M8[D], f8, f8, f8, f8',
converters={1: dmy2ymd})
trend_points = (highest_prices+lowest_prices+closing_prices)/3
days = dates.astype(int)
# =np.column_stack:將一位矩陣以縱向組合
"""
>>> a=[1,2,3];b=[11,22,33];np.column_stack((a,b))
array([[ 1, 11],
[ 2, 22],
[ 3, 33]])
"""
# 同理還有row_stack(),方法與其剛好相反
# np.ones_like() 生成一個與引數矩陣結構相同但值為1的矩陣
a = np.column_stack((days, np.ones_like(days)))
# 生成a,b的組合,暫時不知道多個變數情況下的擬合的公示,查手冊
x = np.linalg.lstsq(a, trend_points)[0]
#print(np.linalg.lstsq(a, trend_points))
# :(array([ 1.81649663e-01, -2.37829793e+03]), array([1267.18780684]), 2, array([8.22882234e+04, 4.62700411e-03]))
#得到的y`的值矩陣
trend_line = days*x[0]+x[1]
mp.figure('Candlestick', facecolor='lightgray')
mp.title('Candlestick', fontsize=20)
mp.xlabel('Date', fontsize=14)
mp.ylabel('Price', fontsize=14)
ax = mp.gca()
# 設定水平座標每個星期一為主刻度
ax.xaxis.set_major_locator(md.WeekdayLocator(
byweekday=md.MO))
# 設定水平座標每一天為次刻度
ax.xaxis.set_minor_locator(md.DayLocator())
# 設定水平座標主刻度標籤格式
ax.xaxis.set_major_formatter(md.DateFormatter(
'%d %b %Y'))
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
dates = dates.astype(md.datetime.datetime)
# 陽線掩碼
rise = closing_prices - opening_prices >= 0.01
# 陰線掩碼
fall = opening_prices - closing_prices >= 0.01
# 填充色
fc = np.zeros(dates.size, dtype='3f4')
fc[rise], fc[fall] = (1, 1, 1), (0, 0.5, 0)
# 邊緣色
ec = np.zeros(dates.size, dtype='3f4')
ec[rise], ec[fall] = (1, 0, 0), (0, 0.5, 0)
mp.bar(dates, highest_prices - lowest_prices, 0,
lowest_prices, color=fc, edgecolor=ec)
mp.bar(dates, closing_prices - opening_prices, 0.8,
opening_prices, color=fc, edgecolor=ec)
mp.plot(dates, trend_line)
# 自動調整水平座標軸的日期標籤
mp.gcf().autofmt_xdate()
mp.show()
裁剪、壓縮和累乘
ndarray.clip(min=下限, max=上限)
將呼叫陣列中小於和大於下限和上限的元素替換為下限和上限,返回裁剪後的陣列,呼叫陣列保持不變。
ndarray.compress(條件)
返回由呼叫陣列中滿足條件的元素組成的新陣列。
ndarray.prod()
返回呼叫陣列中所有元素的乘積——累乘。
ndarray.cumprod()
返回呼叫陣列中所有元素執行累乘的過程陣列。
import numpy as np
a = np.array([10, 20, 30, 40, 50])
print(a)
b = a.clip(min=15, max=45)
print(b)
c = a.compress((15 <= a) & (a <= 45))
print(c)
d = a.prod()
print(d)
e = a.cumprod()
print(e)
def jiecheng(n):
return n if n == 1 else n * jiecheng(n - 1)
n = 5
print(jiecheng(n))
jc = 1
for i in range(2, n + 1):
jc *= i
print(jc)
print(np.arange(2, n + 1).prod())
結果:
[10 20 30 40 50]
[15 20 30 40 45]
[20 30 40]
12000000
[ 10 200 6000 240000 12000000]
120
120
120
相關性

相關性:
相關係數=相關係數
cov_ab/(std_a x std_b)=cov_ba/(std_b x std_a)
協方差矩陣:
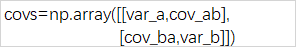
標準差矩陣:

相關性矩陣=協方差矩陣/標準差矩陣:(等號右邊是一個矩陣)
| var_a/(std_a x std_a) cov_ab/(std_a x std_b) |
相關性= | cov_ba/(std_b x std_a) var_b/(std_b x std_b) |
numpy.cov(a, b)->相關矩陣的分子矩陣(協方差矩陣)
numpy.corrcoef(a, b)->相關性矩陣
手動和自動計算的例:
import datetime as dt
import numpy as np
import matplotlib.pyplot as mp
import matplotlib.dates as md
def dmy2ymd(dmy):
dmy = str(dmy, encoding='utf-8')
date = dt.datetime.strptime(
dmy, '%d-%m-%Y').date()
ymd = date.strftime('%Y-%m-%d')
return ymd
dates, bhp_closing_prices = np.loadtxt(
'../../data/bhp.csv', delimiter=',',
usecols=(1, 6), unpack=True,
dtype='M8[D], f8', converters={1: dmy2ymd})
vale_closing_prices = np.loadtxt(
'../../data/vale.csv', delimiter=',',
usecols=(6), unpack=True)
bhp_returns = np.diff(
bhp_closing_prices) / bhp_closing_prices[:-1]
vale_returns = np.diff(
vale_closing_prices) / vale_closing_prices[:-1]
ave_a = bhp_returns.mean()
dev_a = bhp_returns - ave_a
var_a = (dev_a * dev_a).sum() / (dev_a.size - 1)
std_a = np.sqrt(var_a)
ave_b = vale_returns.mean()
dev_b = vale_returns - ave_b
var_b = (dev_b * dev_b).sum() / (dev_b.size - 1)
std_b = np.sqrt(var_b)
cov_ab = (dev_a * dev_b).sum() / (dev_a.size - 1)
cov_ba = (dev_b * dev_a).sum() / (dev_b.size - 1)
#相關係數
corr = np.array([
[var_a / (std_a * std_a), cov_ab / (std_a * std_b)],
[cov_ba / (std_b * std_a), var_b / (std_b * std_b)]])
print(corr)
#相關性矩陣的分子矩陣:協方差矩陣
covs = np.cov(bhp_returns, vale_returns)
#相關性矩陣的分母矩陣:標準差矩陣
stds = np.array([
[std_a * std_a, std_a * std_b],
[std_b * std_a, std_b * std_b]])
corr = covs / stds
print(corr)
corr = np.corrcoef(bhp_returns, vale_returns)
print(corr)
mp.figure('Correlation Of Returns',
facecolor=
