我也只是在學習的過程中，相當於自己理解推導一遍做個筆記，參考了別人很多東西，文末有相關連結。

什麼是邏輯迴歸

邏輯迴歸也叫做對數機率迴歸，但它卻用來做二分類。 線性迴歸產生的預測值為 $z = \theta^{T}x$，線性迴歸通常用來做迴歸。但是可以線上性迴歸基礎上，加上性質像階躍函式但光滑可導的sigmod函式，然後算出一個概率$\widehat{p}$來。如果$\widehat{p}$大於0.5，可以將它判定為一類（比如正例1），小於等於0.5判定為另一類（比如負例0）。

其中，sigmod函式（簡寫為$\sigma$）為： $\sigma(z)=\frac{1}{1+e^{-z}}$

邏輯迴歸，在我看來就是線進行線性迴歸，再在它的基礎上加上sigmod函式，得到一個概率值，進而判斷該樣本屬於哪一類。計算公式如下： $\widehat{p} = \sigma(z) = \sigma(\theta^{T}\cdot x) = h_{\theta}(x)$ 其中，$\theta$是權重，也是我們待求引數。 根據概率值$\widehat{p}$對樣本進行分類： $\widehat{y} =\left\{\begin{matrix} 0 & \widehat{p}<0.5,\\ 1 & \widehat{p}\geq 0.5 \end{matrix}\right.$

邏輯迴歸的代價函式

為了使正樣本得到高的概率值$\widehat{p}$（接近1好），負樣本得到低的概率值$\widehat{p}$（接近0好），從而找出權重引數$\theta$。設計單個樣本的損失函式如下： $c(\theta) =\left\{\begin{matrix} -log(\widehat{p}) & y=1,\\ -log(1 - \widehat{p}) & y=0 \end{matrix}\right.$

極大似然估計

由以上公式，可知任何一個樣本都有： $\left\{\begin{matrix} P(y=1|x;\theta) = h_{\theta}(x)\\ P(y=0|x;\theta) = 1 - h_{\theta}(x) \end{matrix}\right.$

整合一下： $P(y|x;\theta) = h_{\theta}(x) ^{y} (1 - h_{\theta}(x)) ^{1-y}$

那麼，對於所有m個樣本發生的概率是： $L(\theta) = \prod_{i=1}^{m} P(y^{(i)}|x^{(i)};\theta) = \prod_{i=1}^{m} h_{\theta}(x^{(i)}) ^{y^{(i)}} (1 - h_{\theta}(x^{(i)})) ^{1-y^{(i)}}$

取對數： $l(\theta) = log L(\theta) = \sum_{i=1}^{m} [ y^{(i)} log h_{\theta}(x^{(i)}) + (1-y^{(i)})(1 - h_{\theta}(x^{(i)})) ]$

得到的結果實質上和損失函式是一樣的。

利用梯度下降法求引數

sigmod函式有如下性質： $f^{'}(x) = f(x)(1-f(x))$ $J(\theta)$對$\theta$的第j個屬性 求梯度， （公式實在太多了。。copy了一下） 圖片中，下標i表示第i個樣本，上標j表示第j維屬性。

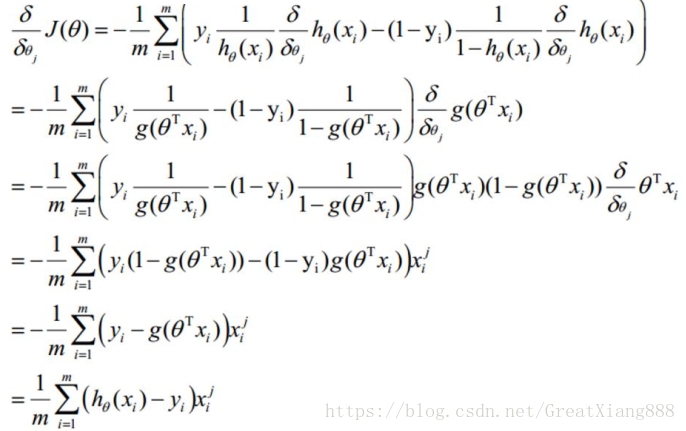
最後，對$\theta$的第j個屬性來說，梯度下降的表示式為： $\theta_{j} := \theta_{j} - \alpha \frac{1}{m} \sum_{i=1}^{m} ( h_{\theta}(x^{(i)}) - y^{(i)} )x_{j}^{(i)}$