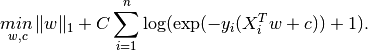引數設定

α：

梯度上升演算法迭代時候權重更新公式中包含 α ：

# 梯度上升演算法-計算迴歸係數  
# 每個迴歸係數初始化為1
# 重複R次：
#    計算整個資料集的梯度
#    使用α*梯度更新迴歸係數的向量
#    返回迴歸係數
def gradAscent(dataMatIn, classLabels,alpha=0.001,maxCycles = 500):  
    dataMatrix = mat(dataMatIn)     #轉換為numpy資料型別  
    labelMat = mat(classLabels).transpose()  
    m,n = shape(dataMatrix)      
    maxCycles = 500
 
  
    weights = ones((n,1))  
    for k in range(maxCycles):  
        h = sigmoid(dataMatrix*weights)  
        error = (labelMat - h)  
        #計算真實類別與預測類別的差值，按照該差值的方向調整迴歸係數
        weights = weights + alpha* dataMatrix.transpose() * error  
    return weights  

λ

λ，正則化引數（泛化能力），加正則化的前提是特徵值要進行歸一化

在實際應該過程中，為了增強模型的泛化能力，防止我們訓練的模型過擬合，特別是對於大量的稀疏特徵，模型複雜度比較高，需要進行降維，我們需要保證在訓練誤差最小化的基礎上，通過加上正則化項減小模型複雜度。在邏輯迴歸中，有L1、L2進行正則化。>
損失函式如下：

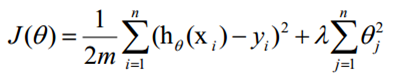
http://www.bkjia.com/yjs/996300.html
在損失函式里加入一個正則化項，正則化項就是權重的L1或者L2範數乘以一個λ，用來控制損失函式和正則化項的比重，直觀的理解，首先防止過擬合的目的就是防止最後訓練出來的模型過分的依賴某一個特徵，當最小化損失函式的時候，某一維度很大，擬合出來的函式值與真實的值之間的差距很小，通過正則化可以使整體的cost變大，從而避免了過分依賴某一維度的結果。當然加正則化的前提是特徵值要進行歸一化。

threshold

threshold變數用來控制分類的閾值，預設值為0.5。表示如果預測值小於threshold則為分類0.0，否則為1.0。

在Spark Java中
ElasticNetParam ： α ；RegParam ：λ。

LogisticRegression lr=new LogisticRegression()
                .setMaxIter(10)
                .setRegParam(0.3)
                .setElasticNetParam(0.2)                
                .setThreshold(0.5);

分類效果評估

混淆矩陣（Confusion matrix）：
考慮一個二分問題，即將例項分成正類（positive）或負類（negative）。對一個二分問題來說，會出現四種情況。如果一個例項是正類並且也被 預測成正類，即為真正類（True positive）,如果例項是負類被預測成正類，稱之為假正類（False positive）。相應地，如果例項是負類被預測成負類，稱之為真負類（True negative）,正類被預測成負類則為假負類（false negative）。
TP：正確肯定的數目；
FN：漏報，沒有正確找到的匹配的數目；
FP：誤報，給出的匹配是不正確的；
TN：正確拒絕的非匹配對數

精確率，precision = TP / (TP + FP)
模型判為正的所有樣本中有多少是真正的正樣本
召回率，recall = TP / (TP + FN)
準確率，accuracy = (TP + TN) / (TP + FP + TN + FN)
反映了分類器統對整個樣本的判定能力——能將正的判定為正，負的判定為負
如何在precision和Recall中權衡？
F1 Score = P*R/2(P+R)，其中P和R分別為 precision 和 recall
在precision與recall都要求高的情況下，可以用F1 Score來衡量

為什麼會有這麼多指標呢？
這是因為模式分類和機器學習的需要。判斷一個分類器對所用樣本的分類能力或者在不同的應用場合時，需要有不同的指標。 當總共有個100 個樣本（P+N=100）時，假如只有一個正例（P=1），那麼只考慮精確度的話，不需要進行任何模型的訓練，直接將所有測試樣本判為正例，那麼 A 能達到 99%，非常高了，但這並沒有反映出模型真正的能力。另外在統計訊號分析中，對不同類的判斷結果的錯誤的懲罰是不一樣的。舉例而言，雷達收到100個來襲導彈的訊號，其中只有 3個是真正的導彈訊號，其餘 97 個是敵方模擬的導彈訊號。假如系統判斷 98 個（97 個模擬訊號加一個真正的導彈訊號）訊號都是模擬訊號，那麼Accuracy=98%，很高了，剩下兩個是導彈訊號，被截掉，這時Recall=2/3=66.67%，Precision=2/2=100%，Precision也很高。但剩下的那顆導彈就會造成災害。

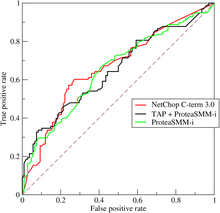
ROC曲線和AUC
有時候我們需要在精確率與召回率間進行權衡，
調整分類器threshold取值，以FPR（假正率False-positive rate）為橫座標，TPR（True-positive rate）為縱座標做ROC曲線；
Area Under roc Curve(AUC)：處於ROC curve下方的那部分面積的大小通常，AUC的值介於0.5到1.0之間，較大的AUC代表了較好的效能；
精確率和召回率是互相影響的，理想情況下肯定是做到兩者都高，但是一般情況下準精確率、召回率就低，召回率低、精確率高，當然如果兩者都低，那是什麼地方出問題了

Spark 2.0分類評估

//獲得迴歸模型訓練的Summary
LogisticRegressionTrainingSummary trainingSummary = lrModel.summary();

// Obtain the loss per iteration.
//每次迭代的損失，一般會逐漸減小
double[] objectiveHistory = trainingSummary.objectiveHistory();
for (double lossPerIteration : objectiveHistory) {
  System.out.println(lossPerIteration);
}

// Obtain the metrics useful to judge performance on test data.
// We cast the summary to a BinaryLogisticRegressionSummary since the problem is a binary
// classification problem.
//強制型別轉換為二類LR的Summary，然後就可以用混淆矩陣,ROC等評估方法了。Spark2.0還無法針對多類
BinaryLogisticRegressionSummary binarySummary =
  (BinaryLogisticRegressionSummary) trainingSummary;

// Obtain the receiver-operating characteristic as a dataframe and areaUnderROC.
Dataset<Row> roc = binarySummary.roc();//獲得ROC
roc.show();//顯示ROC資料表，可以用這個資料自己畫ROC曲線
roc.select("FPR").show();
System.out.println(binarySummary.areaUnderROC());//AUC

// Get the threshold corresponding to the maximum F-Measure and rerun LogisticRegression with
// this selected threshold.
//不同的閾值，計算不同的F1，然後通過最大的F1找出並重設模型的最佳閾值。
Dataset<Row> fMeasure = binarySummary.fMeasureByThreshold();
double maxFMeasure = fMeasure.select(functions.max("F-Measure")).head().getDouble(0);//獲得最大的F1值
double bestThreshold = fMeasure.where(fMeasure.col("F-Measure").equalTo(maxFMeasure))
  .select("threshold").head().getDouble(0);//找出最大F1值對應的閾值（最佳閾值）
lrModel.setThreshold(bestThreshold);//並將模型的Threshold設定為選擇出來的最佳分類閾值

package my.spark.ml.practice.classification;

import org.apache.log4j.Level;
import org.apache.log4j.Logger;
import org.apache.spark.ml.classification.BinaryLogisticRegressionTrainingSummary;
import org.apache.spark.ml.classification.LogisticRegression;
import org.apache.spark.ml.classification.LogisticRegressionModel;
import org.apache.spark.ml.classification.LogisticRegressionTrainingSummary;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.SparkSession;
import org.apache.spark.sql.functions;


public class myLogisticRegression {

    public static void main(String[] args) {
        SparkSession spark=SparkSession
                .builder()
                .appName("LR")
                .master("local[4]")
                .config("spark.sql.warehouse.dir","file///:G:/Projects/Java/Spark/spark-warehouse" )
                .getOrCreate();
        String path="G:/Projects/CgyWin64/home/pengjy3/softwate/spark-2.0.0-bin-hadoop2.6/"
                + "data/mllib/sample_libsvm_data.txt";

        //遮蔽日誌
        Logger.getLogger("org.apache.spark").setLevel(Level.WARN);
        Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF);       

        //Load trainning data
        Dataset<Row> trainning_dataFrame=spark.read().format("libsvm").load(path);      


        LogisticRegression lr=new LogisticRegression()
                .setMaxIter(10)
                .setRegParam(0.3)
                .setElasticNetParam(0.2)                
                .setThreshold(0.5);

        //fit the model
        LogisticRegressionModel lrModel=lr.fit(trainning_dataFrame);

        //print the coefficients and intercept for logistic regression
        System.out.println
        ("Coefficient:"+lrModel.coefficients()+"Itercept"+lrModel.intercept());

        //Extract the summary from the returned LogisticRegressionModel
        LogisticRegressionTrainingSummary summary=lrModel.summary();

        //Obtain the loss per iteration.
        double[] objectiveHistory=summary.objectiveHistory();
        for(double lossPerIteration:objectiveHistory){
            System.out.println(lossPerIteration);
        }
        // Obtain the metrics useful to judge performance on test data.
        // We cast the summary to a BinaryLogisticRegressionSummary since the problem is a binary
        // classification problem.
        BinaryLogisticRegressionTrainingSummary binarySummary=
                (BinaryLogisticRegressionTrainingSummary)summary;
        //Obtain the receiver-operating characteristic as a dataframe and areaUnderROC.
        Dataset<Row> roc=binarySummary.roc();
        roc.show((int) roc.count());//顯示全部的資訊，roc.show()預設只顯示20行
        roc.select("FPR").show();
        System.out.println(binarySummary.areaUnderROC());

        // Get the threshold corresponding to the maximum F-Measure and rerun LogisticRegression with
        // this selected threshold.
        Dataset<Row> fMeasure = binarySummary.fMeasureByThreshold();
        double maxFMeasure = fMeasure.select(functions.max("F-Measure")).head().getDouble(0);
        double bestThreshold = fMeasure.where(fMeasure.col("F-Measure").equalTo(maxFMeasure))
          .select("threshold").head().getDouble(0);
        lrModel.setThreshold(bestThreshold);            
    }

}

BinaryClassificationEvaluator

除了上述Logistic迴歸結果評估方法，在Spark2.0中，二分問題結果評估用BinaryClassificationEvaluator。
引數：
（1）labelCol: label column name (default: label, current: label)
（2）metricName: metric name in evaluation (areaUnderROC|areaUnderPR) (default: areaUnderROC)
看來是沒有其它的評估方法
（3）rawPredictionCol: raw prediction (a.k.a. confidence) column name (default: rawPrediction, current: prediction)：注意名字不是PredictionCol，
只有這三個引數可以設定！
自定義accuracy

//自定義計算accuracy，
        Dataset<Row> predictDF=naiveBayesModel.transform(test);    

        double total=(double) predictDF.count();
        Encoder<Double> doubleEncoder=Encoders.DOUBLE();        
        Dataset<Double> accuracyDF=predictDF.map(new MapFunction<Row,Double>() {            
            @Override
            public Double call(Row row) throws Exception {
                if((double)row.get(0)==(double)row.get(6)){return 1.0;}
                else {return 0.0;}
            }
        }, doubleEncoder);
        accuracyDF.createOrReplaceTempView("view");
        double correct=(double) spark.sql("SELECT value FROM view WHERE value=1.0").count();
        System.out.println("accuracy "+(correct/total));

Scikit

關鍵程式碼分析

#For L1 penalization sklearn.svm.l1_min_c allows to calculate the
#lower bound for C in order to get a non “null” (all feature 
#weights to zero) model. 
#計算一個C的下限值，然後放大到一個區間內。
cs = l1_min_c(X, y, loss='log') * np.logspace(0, 3)

print("l1_min_c=%.4f"%l1_min_c(X, y, loss='log'))
#輸出結果:l1_min_c=0.0143

clf = linear_model.LogisticRegression(C=1.0, penalty='l1', tol=1e-6)
coefs_ = []
for c in cs:#迴圈不同的C
    clf.set_params(C=c)#重新設定C
    clf.fit(X, y)#重新計算
    coefs_.append(clf.coef_.ravel().copy())#獲得係數
    print("score %.4f" % clf.score(X, y))#計算分類的score
coefs_ = np.array(coefs_)#將係數轉為np.array
plt.plot(np.log10(cs), coefs_)#作圖 log(C)vs Coefs

關鍵引數C，penalty
penalty選擇’l1’，’l2’
C：large values of C give more freedom to the model. Conversely, smaller values of C constrain the model more（C，也控制著模型的泛化能力，與前面Spark中所說的RegParam -λ作用類似）

Scikit中的LR可以完成多類（one-vs-rest）的分類，L1或L2正則化。

This implementation can fit a multiclass (one-vs-rest) logistic regression with optional L2 or L1 regularization.
binary class L2 penalized logistic regression minimizes the following cost function：

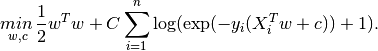
L1 regularized logistic regression solves the following optimization problem

不同情形演算法選擇：
Small dataset or L1 penalty —-> “liblinear”
Multinomial loss —–> “lbfgs” or newton-cg”
Large dataset —–> “sag”

“Sag”：隨機平均梯度下降演算法，Stochastic Average Gradient descent ，在大資料集上通常比其它演算法要快。

It does not handle “multinomial” case, and is limited to L2-penalized
models, yet it is often faster than other solvers for large datasets,
when both the number of samples and the number of features are large.
Stochastic gradient descent is a simple yet very efficient approach to fit linear models. It is particularly useful when the number of samples (and the number of features) is very large.

完整的程式碼如下：

print(__doc__)

# Author: Alexandre Gramfort <[email protected]>
# License: BSD 3 clause

from datetime import datetime
import numpy as np
import matplotlib.pyplot as plt

from sklearn import linear_model
from sklearn import datasets
from sklearn.svm import l1_min_c

iris = datasets.load_iris()
X = iris.data
y = iris.target

X = X[y != 2]
y = y[y != 2]

X -= np.mean(X, 0)

###############################################################################
# Demo path functions

cs = l1_min_c(X, y, loss='log') * np.logspace(0, 3)

print("Computing regularization path ...")
start = datetime.now()
clf = linear_model.LogisticRegression(C=1.0, penalty='l1', tol=1e-6)
coefs_ = []
for c in cs:
    clf.set_params(C=c)
    clf.fit(X, y)
    coefs_.append(clf.coef_.ravel().copy())
print("This took ", datetime.now() - start)

coefs_ = np.array(coefs_) #50*4維矩陣
plt.plot(np.log10(cs), coefs_)
ymin, ymax = plt.ylim()
plt.xlabel('log(C)')
plt.ylabel('Coefficients')
plt.title('Logistic Regression Path')
plt.axis('tight')
plt.show()