影象處理之影象去噪
假設影象退化過程被建模為一個退化函式和一個加性噪聲項,對輸入影象f(x,y)進行處理,產生退化後的影象g(x,y)。給定g(x,y)和退化函式H以及關於加性噪聲項的一些知識,影象復原的目的就是獲得原始影象的一個估計
。
空間域的退化影象:
其中h(x,y)是退化函式的空間表示,表示卷積。
等價的頻率域表示為:
下圖是影象退化/復原過程的模型:
噪聲概率密度函式
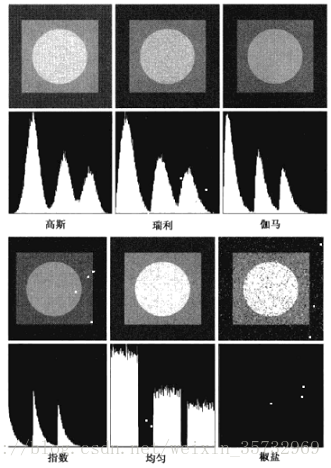
考慮加性噪聲,我們關心的是這個噪聲分量中灰度值的統計特性,用概率密度函式(PDF)表徵。下面是一些重要的噪聲概率密度函式影象及說明:
高斯噪聲:
其中,z表示灰度值,表示z的平均值,
表示z的標準差(
為方差),其值約有70%落在範圍
瑞利噪聲:
其中,概率密度的均值和方差為:
愛爾蘭(伽馬)噪聲:
其中,a>0,b為正整數,概率密度均值和方差為:
指數噪聲:
其中a>0,概率密度均值和方差為:
它是當b=1時愛爾蘭PDF的特殊情況。
均勻噪聲:
其中,概率密度的均值和方差為:
脈衝噪聲(椒鹽噪聲,胡椒(黑)+鹽粉(白)):
如果b>a,則灰度級b在影象中顯示為一個亮點,灰度級a顯示為暗點。若或
為0,則脈衝噪聲為單極脈衝,若均不為0,則稱為雙極脈衝(也叫椒鹽噪聲,散粒噪聲,尖峰噪聲)。
高斯噪聲源於如電子電路噪聲、低照明度或高溫帶來的感測器噪聲;指數密度和伽馬密度在鐳射成像中有用;脈衝噪聲在快速過渡的情況下產生。
原影象:
新增不同噪聲後的影象:
噪聲引數的估計
通常由合理的恆定灰度值的一小部分來估計PDF的引數。
下圖的直方圖使用左上角的小條帶的影象資料計算的,這些小條帶分別來自上圖的高斯、瑞利和均勻噪聲影象。
可以用來自影象條帶的資料計算灰度級的均值和方差。令表示條帶S中畫素灰度的概率估計,則S的均值和方差如下:
觀察直方圖的形狀可確定最接近的PDF匹配。如果形狀近似於高斯,那麼均值和方差就是我們所需要確定引數;如果是其他形狀,那麼我們可以用均值和方差求出引數a和b。對於脈衝噪聲,我們要估計的是黑白像素髮生的實際概率,這需要一個相對恆定的中等灰度區域來計算直方圖,圖中黑白畫素尖峰的高度就是脈衝噪聲中
空間域去噪(僅存在噪聲退化)
當一幅影象中唯一存在的退化是噪聲時,根據前面的定義,退化影象相應地變為:
均值濾波器
算術均值濾波器:
其中,是退化影象,
是得到的復原影象,
表示中心在點(x,y)處、大小為m*n的矩形領域的一組座標。
幾何均值濾波器:
這種處理比幾何均值濾波器丟失的細節更少。
算術均值濾波器和幾何均值濾波器適合處理高斯或均勻隨機噪聲。
諧波均值濾波器:
它對於鹽粒噪聲效果較好,不適用於胡椒噪聲。
逆諧波均值濾波器:
Q稱為濾波器的階數。當Q為正時,消除胡椒噪聲;Q為負時,消除鹽粒噪聲;當Q=0時,逆諧波均值濾波器簡化為算術均值濾波器;當Q=-1時,則為諧波均值濾波器。它有一個缺點,必須知道噪聲是暗噪聲還是亮噪聲,以便確定Q的正負。
統計排序濾波器
中值濾波器:
它對脈衝噪聲很有效。
最大值和最小值濾波器:
最大值濾波器對發現影象中最亮點很有效,最小值濾波器對發現影象中最暗點很有效。
中點濾波器:
它對隨機分佈的噪聲有效,如高斯噪聲、均勻噪聲。
修正的阿爾法均值濾波器:
假設在鄰域內去掉g(s,t)最低灰度值的d/2個畫素和最高灰度值的d/2個畫素,令
代表剩下的mn-d個畫素,由這些剩餘畫素的平均值形成的濾波器稱為修正的阿爾法均值濾波器:
d的取值範圍可為0到mn-1。當d=0時,它變為算術均值濾波器;當d = mn-1時,它變為中值濾波器;當d取其他值時,它在包括多種噪聲的情況下很有用,如高斯噪聲和椒鹽噪聲的混合。
自適應濾波器
自適應區域性降低噪聲濾波器在區域性區域中心任意一點(x,y)上的響應基於以下4個量:
- g(x,y),帶噪影象在(x,y)上的值;
,汙染f(x,y)形成g(x,y)的噪聲方差;
,
中畫素的均值;
,
中畫素的區域性方差。
我們希望的濾波器效能如下:
- 如果
,則濾波器應該簡單的返回g(x,y)的值;
- 如果區域性方差
與
是高度相關的,則濾波器返回g(x,y)的一個近似值。典型的,高區域性方差與邊緣相關,應該保護這些邊緣;
- 如果兩個方差相等,希望返回
中畫素的算術平均。這種情況發生在區域性區域與整個影象有相同特性的條件下,區域性區域的噪聲將通過求平均降低。
根據這些假設,得到如下表達式:
需要知道或估計的量是全部噪聲的方差,其他引數通過
計算。這裡隱含的假設條件是
,實際中可能違反這個條件,當
時,可以把比率設為1。
自適應中值濾波器:如果脈衝噪聲空間密度不大,中值濾波器效能會很好(根據經驗,小於0.2).而自適應中值濾波器可以處理更大密度的脈衝噪聲,它在進行濾波處理時會根據某些條件改變(或增大)
的尺寸。
記以下符號:
=
中最小灰度值;
=
中最大灰度值;
=
中灰度值的中值;
= 座標(x,y)處的灰度值;
=
允許的最大尺寸。
自適應中值濾波器演算法以兩個過程工作:
程序A:
如果且
,則轉到程序B
否則增大視窗尺寸
如果視窗尺寸,則重複程序A
否則輸出
程序B:
如果且
,則輸出
否則輸出
該演算法主要有3個目的:
- 去除椒鹽(脈衝)噪聲;
- 平滑其他非脈衝噪聲;
- 減少如物體邊界細化或粗化等失真
程序A的主要目的是確定中值濾波器的輸出是否是一個脈衝。如果有效,則
不是脈衝,轉到程序B,看
是否是一個脈衝,若
,
就不是脈衝,這種情況下, 演算法輸出不變的畫素值
。通過不改變這些中間灰度級的點,減少影象中的失真。如果條件
且
為假,則
或
。這種情況下,畫素值都是一個極端值,演算法輸出中值
,從程序A可知
不是脈衝。若程序A找到一個脈衝,
或
,演算法會增大視窗尺寸並重復程序A,直到找到一個非脈衝中值(並跳到程式B)或達到最大視窗值。如果達到最大視窗值,則返回
(不能保證不是一個脈衝)。
頻率域濾波消除週期噪聲
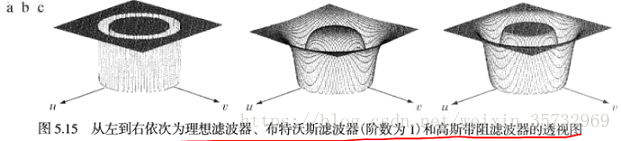
帶阻濾波器:主要應用之一是在頻率域噪聲分量的一般位置近似已知的應用中消除噪聲,一個典型的例子是一幅被加性週期噪聲汙染的影象。
帶通濾波器:與帶阻濾波器相反的操作。通常不會在一幅影象上直接執行帶通濾波,因為這樣會消除太多影象細節。
餡波濾波器:阻止或通過事先定義的中心頻率的鄰域內的頻率。
參考資料:岡薩雷斯《數字影象處理》