進一步優化梯度下降

現在我們要討論用於進一步優化梯度下降的各種演算法。

1. 動量梯度下降法（Momentum）

SGD方法中的高方差振盪使得網路很難穩定收斂，所以有研究者提出了一種稱為動量（Momentum）的技術，通過優化相關方向的訓練和弱化無關方向的振盪，來加速SGD訓練。換句話說，這種新方法將上個步驟中更新向量的分量’γ’新增到當前更新向量。

V(t)=γV(t−1)+η∇(θ).J(θ)

最後通過θ=θ−V(t)來更新引數。

動量項γ通常設定為0.9，或相近的某個值。

這裡的動量與經典物理學中的動量是一致的，就像從山上投出一個球，在下落過程中收集動量，小球的速度不斷增加。

在引數更新過程中，其原理類似：

1)使網路能更優和更穩定的收斂；

2)減少振盪過程。

當其梯度指向實際移動方向時，動量項γ增大；當梯度與實際移動方向相反時，γ減小。這種方式意味著動量項只對相關樣本進行引數更新，減少了不必要的引數更新，從而得到更快且穩定的收斂，也減少了振盪過程。

2. 加速梯度下降法（Nesterov Momentum）

一位名叫Yurii Nesterov研究員，認為動量方法存在一個問題：

如果一個滾下山坡的球，盲目沿著斜坡下滑，這是非常不合適的。一個更聰明的球應該要注意到它將要去哪，因此在上坡再次向上傾斜時小球應該進行減速。

實際上，當小球達到曲線上的最低點時，動量相當高。由於高動量可能會導致其完全地錯過最小值，因此小球不知道何時進行減速，故繼續向上移動。

Yurii Nesterov在1983年發表了一篇關於解決動量問題的論文，因此，我們把這種方法叫做Nestrov梯度加速法。

在該方法中，他提出先根據之前的動量進行大步跳躍，然後計算梯度進行校正，從而實現引數更新。這種預更新方法能防止大幅振盪，不會錯過最小值，並對引數更新更加敏感。

Nesterov梯度加速法（NAG）是一種賦予了動量項預知能力的方法，通過使用動量項γV(t−1)來更改引數θ。通過計算θ−γV(t−1)，得到下一位置的引數近似值，這裡的引數是一個粗略的概念。因此，我們不是通過計算當前引數θ的梯度值，而是通過相關引數的大致未來位置，來有效地預知未來：

V(t)=γV(t−1)+η∇(θ)J( θ−γV(t−1)

然後使用θ=θ−V(t)來更新引數。

現在，我們通過使網路更新與誤差函式的斜率相適應，並依次加速SGD，也可根據每個引數的重要性來調整和更新對應引數，以執行更大或更小的更新幅度。

3. Adagrad方法

Adagrad方法是通過引數來調整合適的學習率η，對稀疏引數進行大幅更新和對頻繁引數進行小幅更新。因此，Adagrad方法非常適合處理稀疏資料。

在時間步長中，Adagrad方法基於每個引數計算的過往梯度，為不同引數θ設定不同的學習率。

先前，每個引數θ(i)使用相同的學習率，每次會對所有引數θ進行更新。在每個時間步t中，Adagrad方法為每個引數θ選取不同的學習率，更新對應引數，然後進行向量化。為了簡單起見，我們把在t時刻引數θ(i)的損失函式梯度設為g(t,i)。

圖3：引數更新公式

Adagrad方法是在每個時間步中，根據過往已計算的引數梯度，來為每個引數θ(i)修改對應的學習率η。

Adagrad方法的主要好處是，不需要手工來調整學習率。大多數引數使用了預設值0.01，且保持不變。

Adagrad方法的主要缺點是，學習率η總是在降低和衰減。

因為每個附加項都是正的，在分母中累積了多個平方梯度值，故累積的總和在訓練期間保持增長。這反過來又導致學習率下降，變為很小數量級的數字，該模型完全停止學習，停止獲取新的額外知識。

因為隨著學習速度的越來越小，模型的學習能力迅速降低，而且收斂速度非常慢，需要很長的訓練和學習，即學習速度降低。

另一個叫做Adadelta的演算法改善了這個學習率不斷衰減的問題。

4. AdaDelta方法

這是一個AdaGrad的延伸方法，它傾向於解決其學習率衰減的問題。Adadelta不是累積所有之前的平方梯度，而是將累積之前梯度的視窗限制到某個固定大小w。

與之前無效地儲存w先前的平方梯度不同，梯度的和被遞迴地定義為所有先前平方梯度的衰減平均值。作為與動量項相似的分數γ，在t時刻的滑動平均值Eg⊃2;僅僅取決於先前的平均值和當前梯度值。

Eg⊃2;=γ.Eg⊃2;+(1−γ).g⊃2;(t)，其中γ設定為與動量項相近的值，約為0.9。

Δθ(t)=−η⋅g(t,i).

θ(t+1)=θ(t)+Δθ(t)

圖4：引數更新的最終公式

AdaDelta方法的另一個優點是，已經不需要設定一個預設的學習率。

目前已完成的改進

1)為每個引數計算出不同學習率；

2) 也計算了動量項momentum；

3)防止學習率衰減或梯度消失等問題的出現。

還可以做什麼改進？

在之前的方法中計算了每個引數的對應學習率，但是為什麼不計算每個引數的對應動量變化並獨立儲存呢？這就是Adam演算法提出的改良點。

Adam演算法

Adam演算法即自適應時刻估計方法（Adaptive Moment Estimation），能計算每個引數的自適應學習率。這個方法不僅儲存了AdaDelta先前平方梯度的指數衰減平均值，而且保持了先前梯度M(t)的指數衰減平均值，這一點與動量類似：

M(t)為梯度的第一時刻平均值，V(t)為梯度的第二時刻非中心方差值。

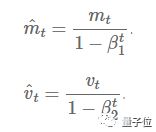
圖5：兩個公式分別為梯度的第一個時刻平均值和第二個時刻方差

則引數更新的最終公式為：

圖6：引數更新的最終公式

其中，β1設為0.9，β2設為0.9999，ϵ設為10-8。

在實際應用中，Adam方法效果良好。與其他自適應學習率演算法相比，其收斂速度更快，學習效果更為有效，而且可以糾正其他優化技術中存在的問題，如學習率消失、收斂過慢或是高方差的引數更新導致損失函式波動較大等問題。

對優化演算法進行視覺化

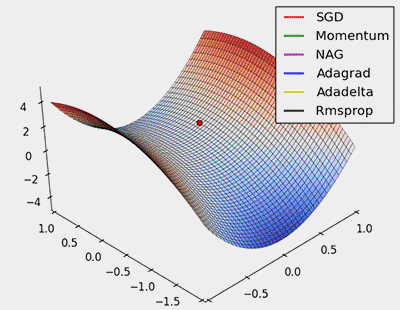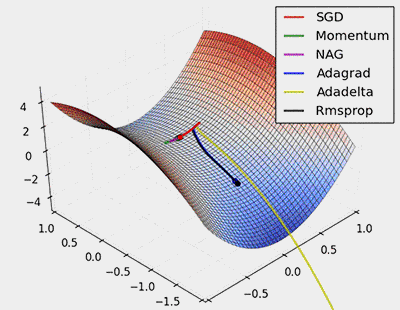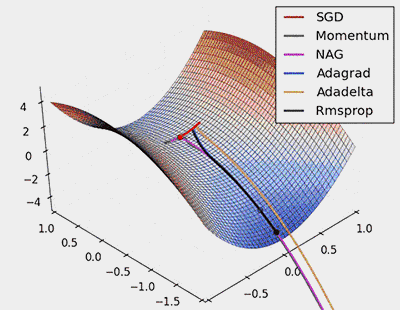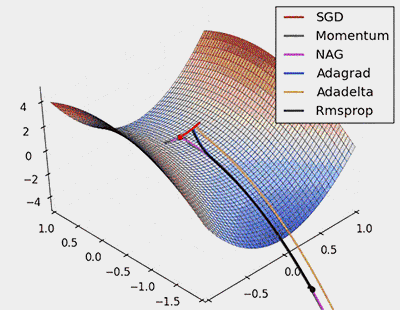
圖8：對鞍點進行SGD優化

從上面的動畫可以看出，自適應演算法能很快收斂，並快速找到引數更新中正確的目標方向；而標準的SGD、NAG和動量項等方法收斂緩慢，且很難找到正確的方向。

結論

我們應該使用哪種優化器？

在構建神經網路模型時，選擇出最佳的優化器，以便快速收斂並正確學習，同時調整內部引數，最大程度地最小化損失函式。

Adam在實際應用中效果良好，超過了其他的自適應技術。

如果輸入資料集比較稀疏，SGD、NAG和動量項等方法可能效果不好。因此對於稀疏資料集，應該使用某種自適應學習率的方法，且另一好處為不需要人為調整學習率，使用預設引數就可能獲得最優值。

如果想使訓練深層網路模型快速收斂或所構建的神經網路較為複雜，則應該使用Adam或其他自適應學習速率的方法，因為這些方法的實際效果更優。

希望你能通過這篇文章，很好地理解不同優化演算法間的特性差異。

相關連結：

二階優化演算法：

https://web.stanford.edu/class/msande311/lecture13.pdf

Nesterov梯度加速法：http://cs231n.github.io/neural-networks-3/

================Adam部分說真的，看的還有點暈，數學底子不行啊，下次再補吧==============

看這篇文章，對Adam演算法有個巨集觀的認識，但具體細節寫的不好。

其中，RMSprop是一個未被髮表的自適應學習率的演算法，該演算法由Geoff Hinton在其Coursera課堂的課程6e中提出。

RMSprop和Adadelta在相同的時間裡被獨立的提出，都起源於對Adagrad的極速遞減的學習率問題的求解。2個人其實就是寫法不一樣，實際上2個公式是一樣的。有些文章喜歡寫成RMSprop代替Adadelta。2個最終的公式移項就是一個加法，一個寫成減法

以下三篇寫的很周到，尤其第3篇裡面帶參考連結

以下2篇專門講Adam，