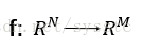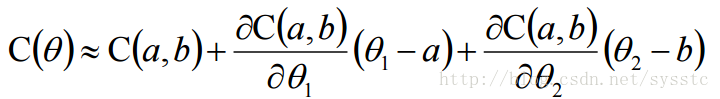深度學習筆記——理論與推導之概念,成本函式與梯度下降演算法初識(一)
阿新 • • 發佈:2018-12-30
前情提要
一、神經網路介紹
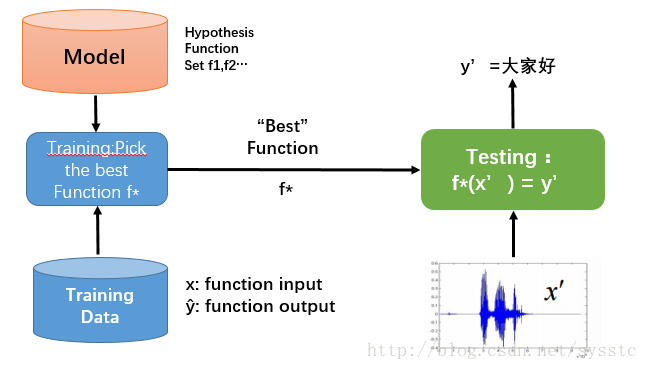
- 概念:Learning ≈ Looking for a Function
- 框架(Framework):
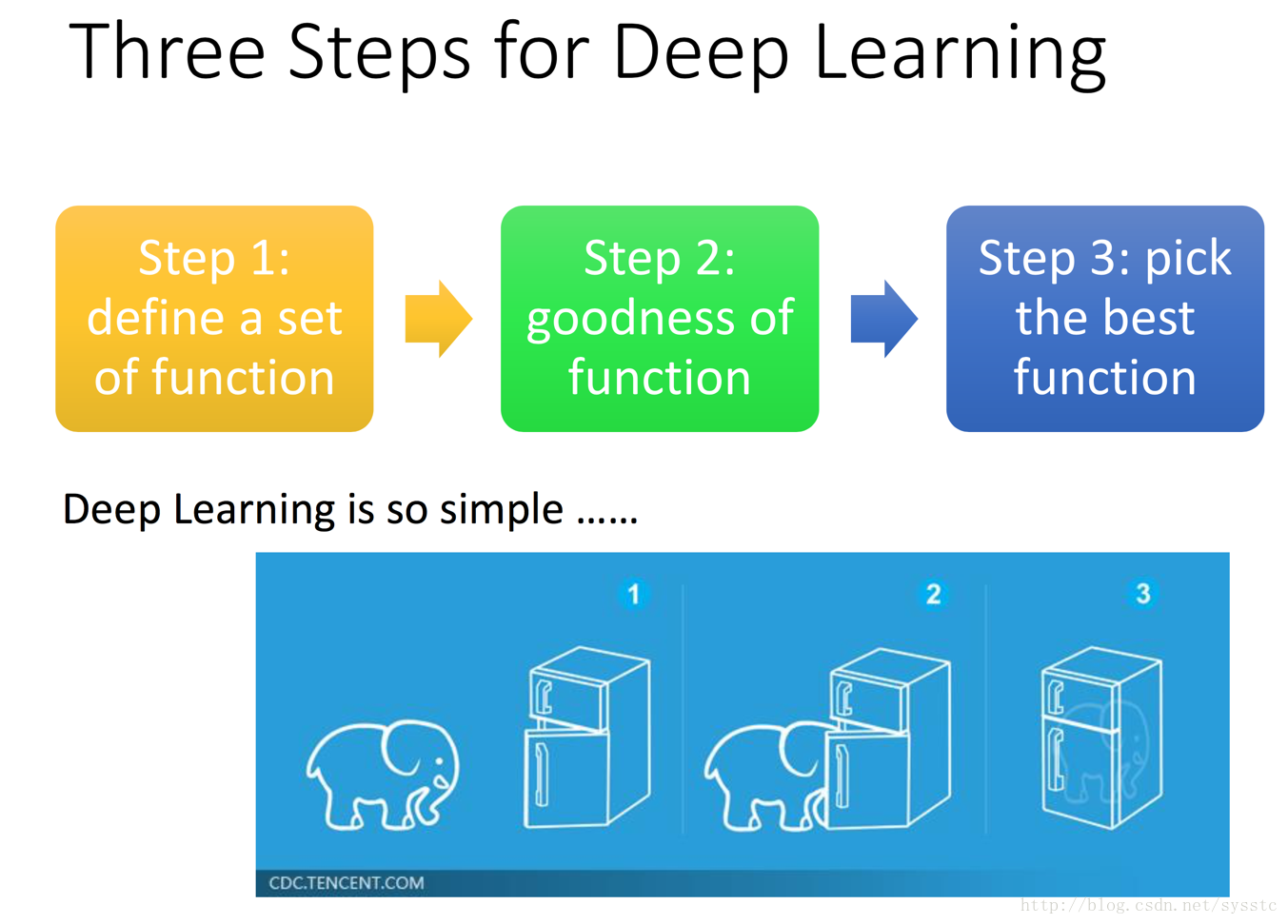
What is Deep Learning?
深度學習其實就是一個定義方法、判斷方法優劣、挑選最佳的方法的過程:
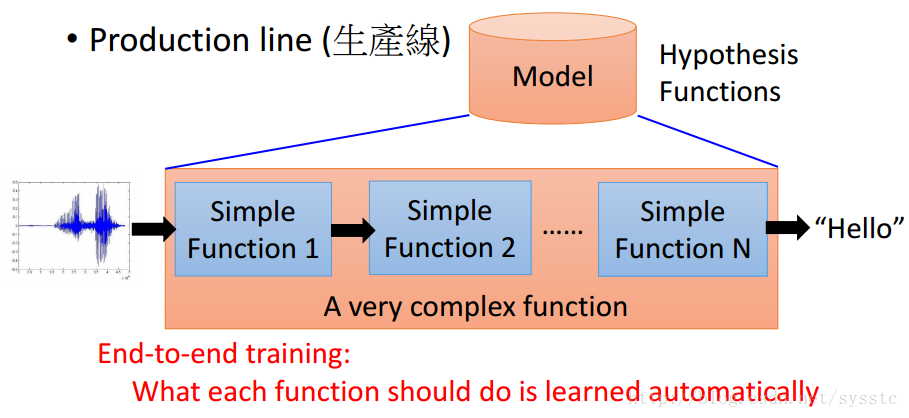
我們可以將nn定義成一個生產線(production line)
- 比起過去的語音識別技術,DeepLearning的所有function都是從資料中進行學習的。
- 深度學習通常指基於神經網路的方法。
二、神經網路的簡單理解:
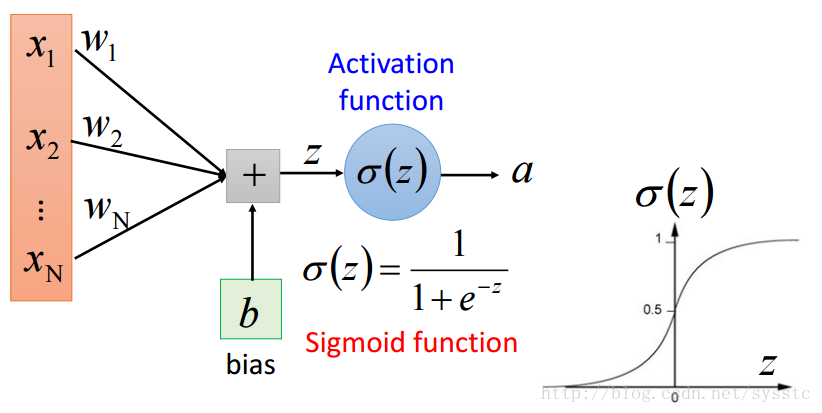
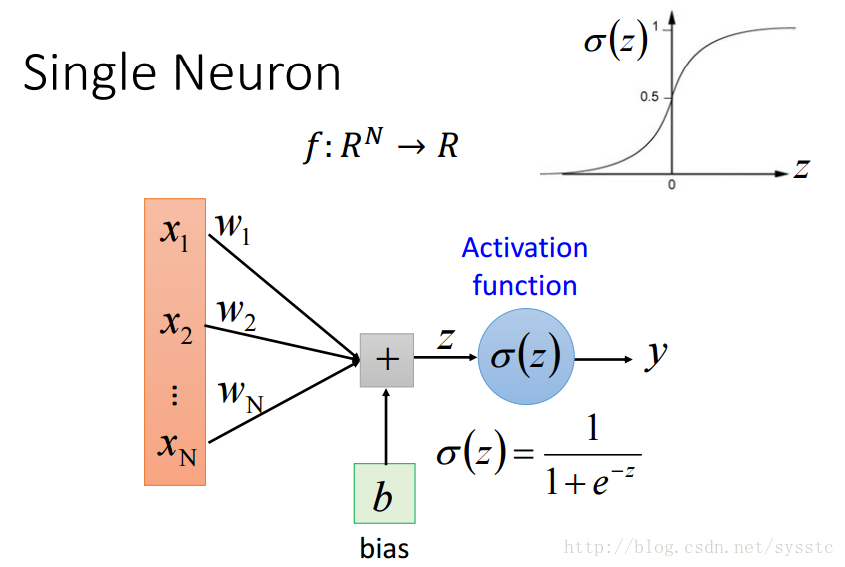
- 每一個神經元都可以看成一個簡單的函式:
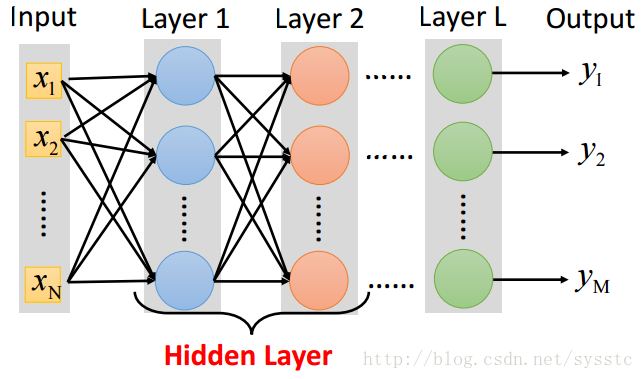
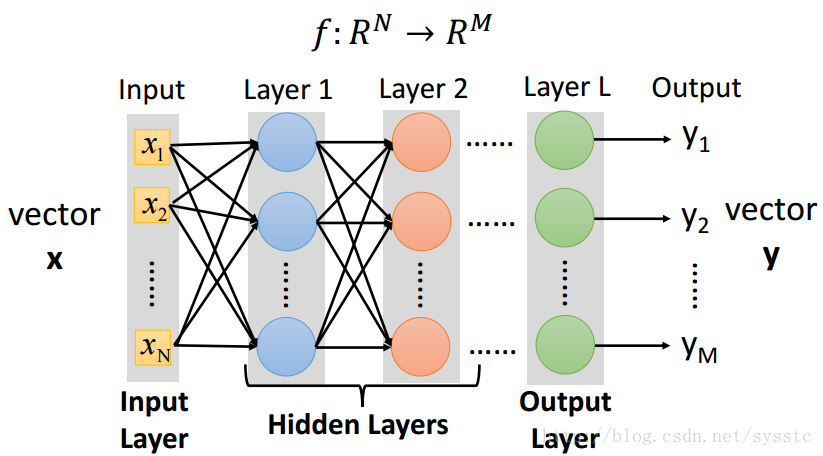
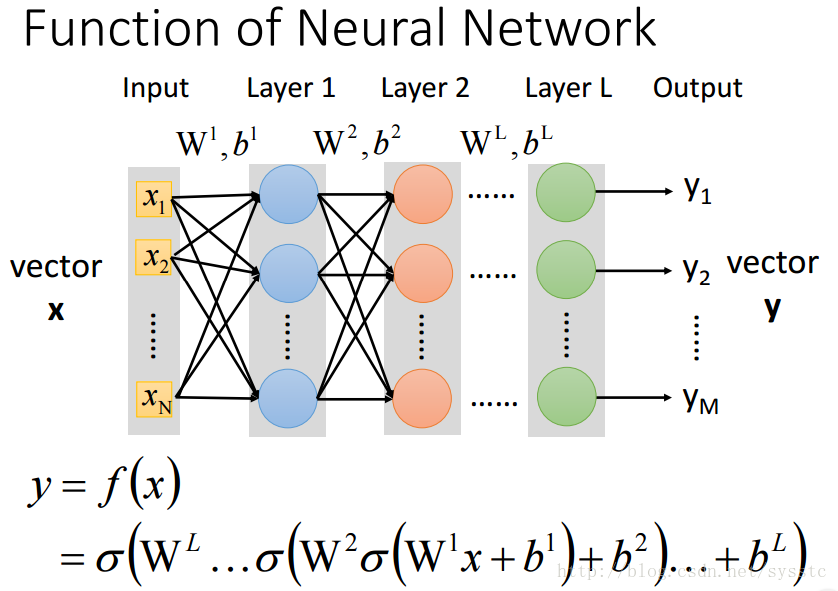
- 一個神經網路都是一個複雜的函式(從一個N維到M維的函式):
- 將神經元級聯起來就可以組成一個神經網路,每一層都是production line上的一個簡單函式。
- 將神經元級聯起來就可以組成一個神經網路,每一層都是production line上的一個簡單函式。
- 為什麼要深度神經網路:
- Universality Theorem:如果給定足夠的neurons,任何一個R^N指向R^M的問題都能被解決。
- 多層神經網路的效果,比一層多個的神經元的神經網路的效果要好的多。
- Deeper:使用更少的引數就能達到與一層多個神經元的神經網路相同的效果。而更多引數也就意味著需要更多的training data。
- 有一些function用deep structure會更好
Neural Network的基礎概念
目錄
- 如何定義方法集
- 判斷方法優劣
- 挑選最佳的方法
考慮的問題:
- 分類問題:
- Binary Classification(二分類問題):target只有兩個,例如:yes/no等
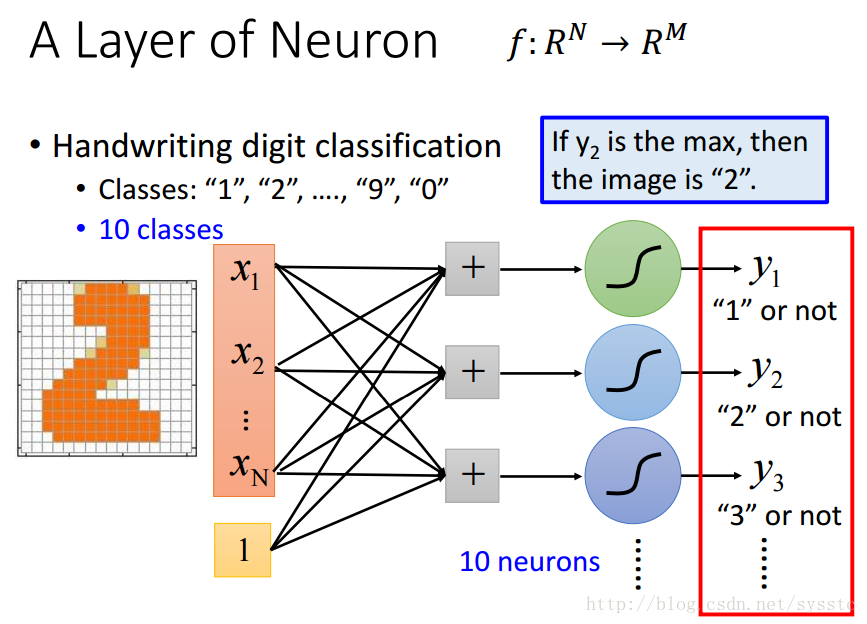
- Multi-class Classification(多分類問題):target有多個但是可以列舉,例如:手寫數字識別等,注意:真的語言識別問題不是一個多分類問題,因為target是不可以列舉的
如何定義方法集?
- 我們想要的是什麼函式:
- 對於一個分類問題:
- 我們想要的函式y = f(x),是可以將問題中的N維轉化成target的M維。
- 輸入x和輸出y可以被表達成一個固定長度的向量,其中x是一個N維向量,y是一個M維向量。
- 對於一個分類問題:
- 單一神經元:
單一神經元只能用來判斷二分類問題,並不能來判斷多分類問題。 - 一層神經網路(一個hidden layer):
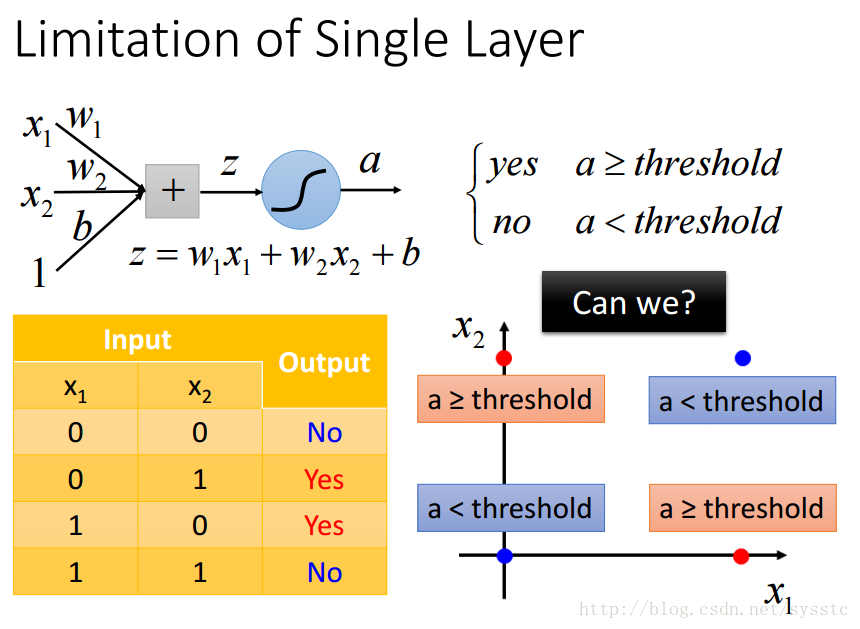
- 單一神經元的限制:
- 單一神經元不能解決以下問題:
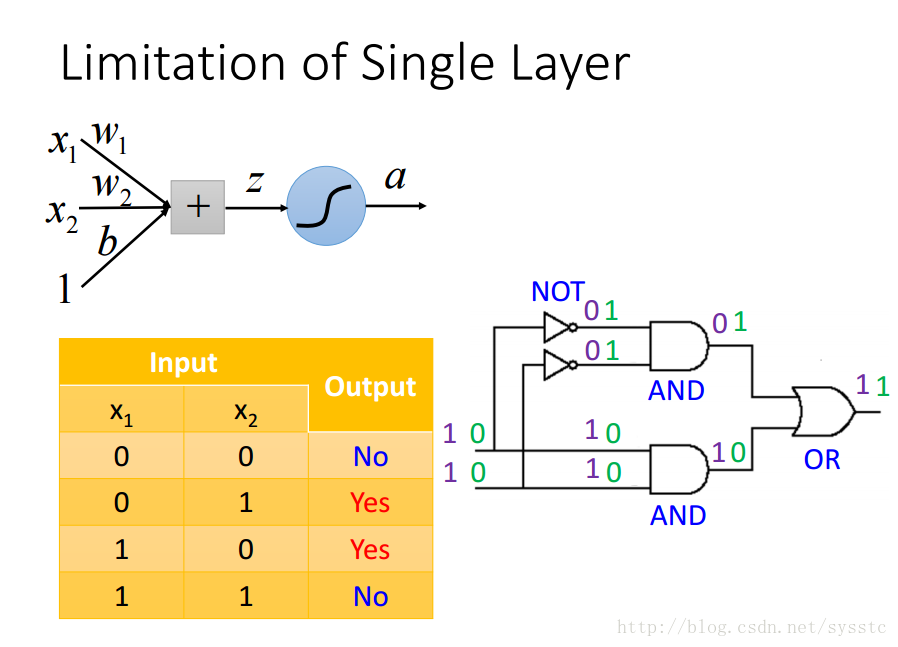
- 參照logic circuit解決這個問題:
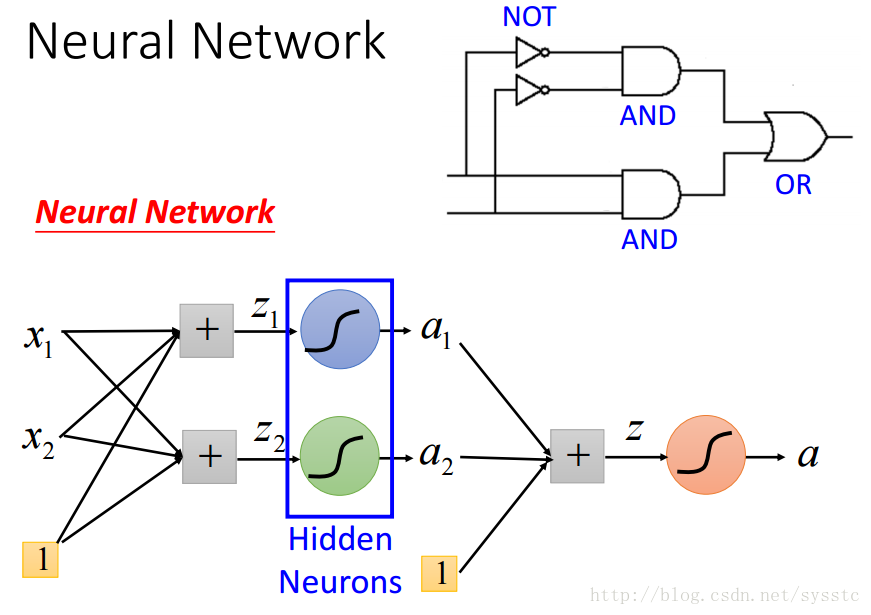
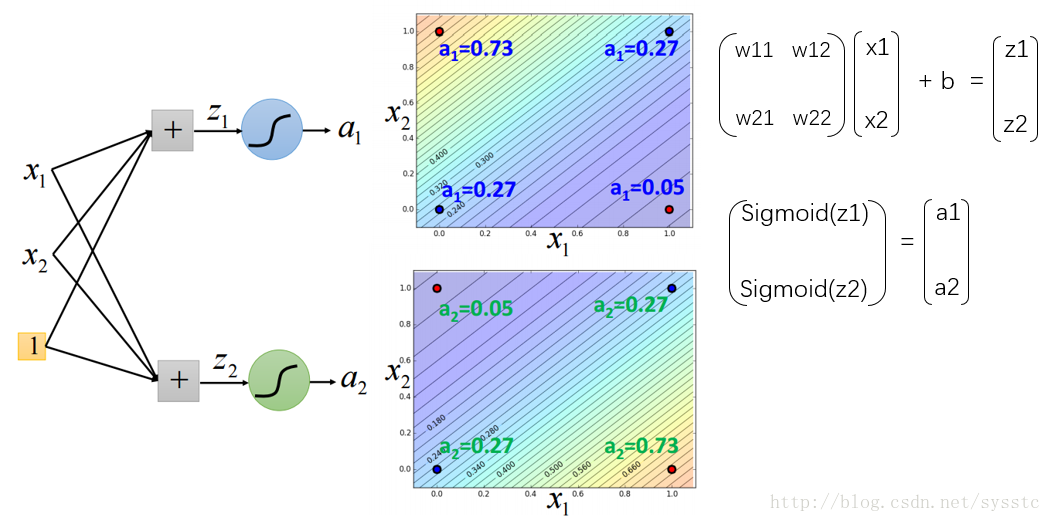
在Hidden layer中加入兩個hidden neurons:
這樣我們可以通過以下計算方法得到第一層的輸出,a1,a2:
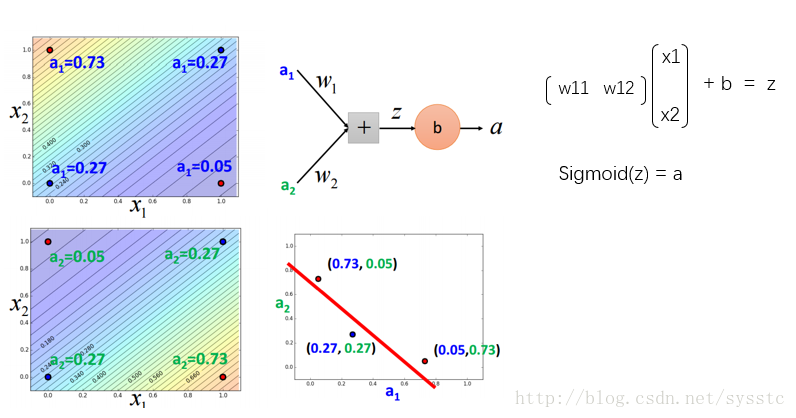
輸出層:
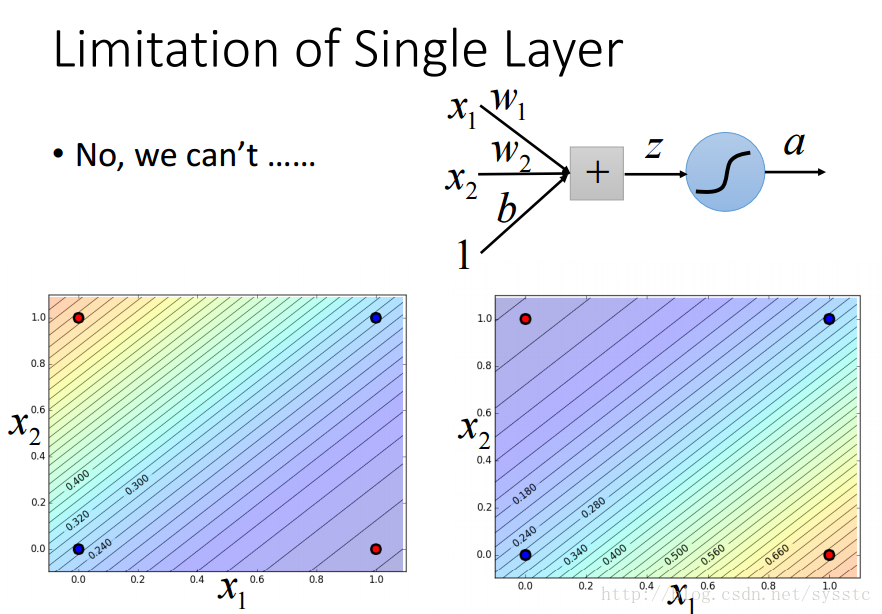
- 單一神經元不能解決以下問題:
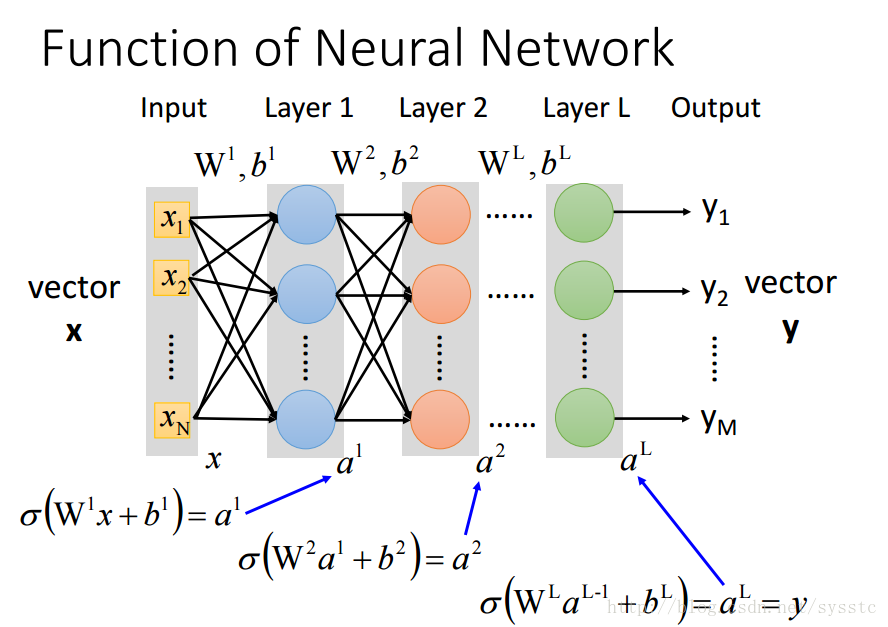
- Neural Network
- Neural Network就像是一個模型,如下圖所示,是一個全連線前向傳播網路,深度神經網路就是有好多隱藏層。
- 概念:
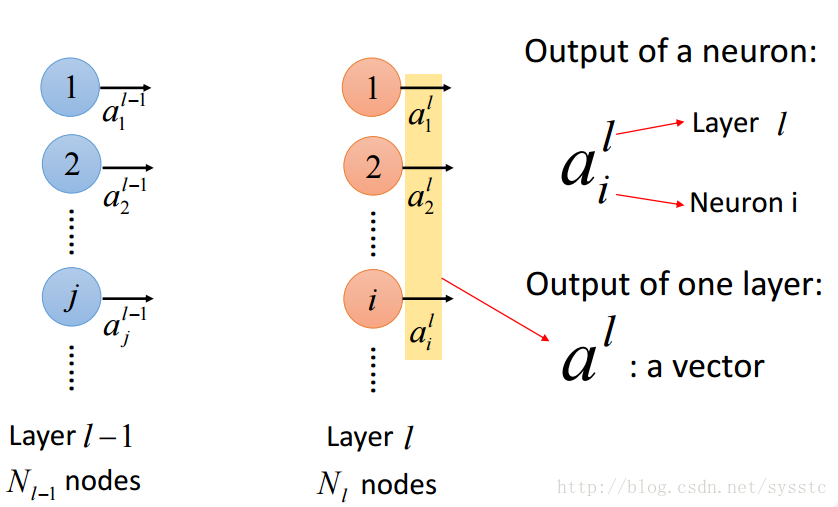
- 啟用函式的輸出a:
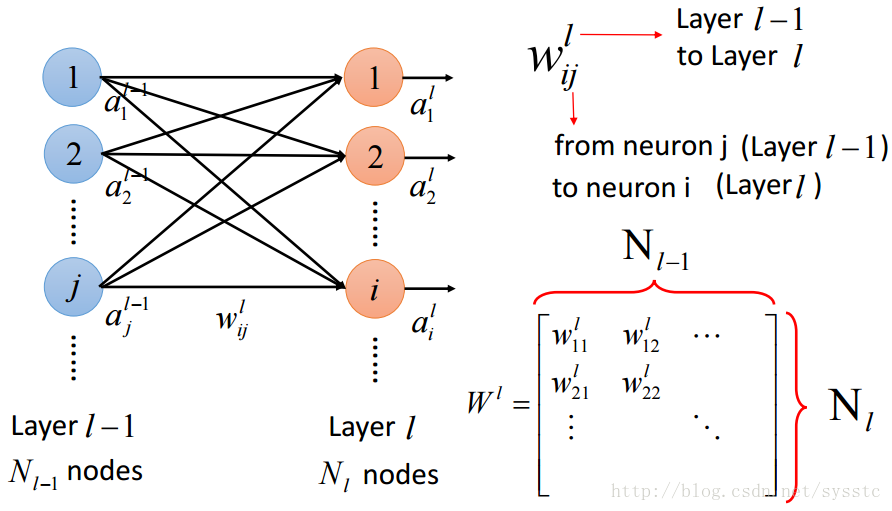
- 權重w:
這裡要注意的是w的下標i,j與上標l,表示的是從第l-1層的神經元j指向第l層的神經元i
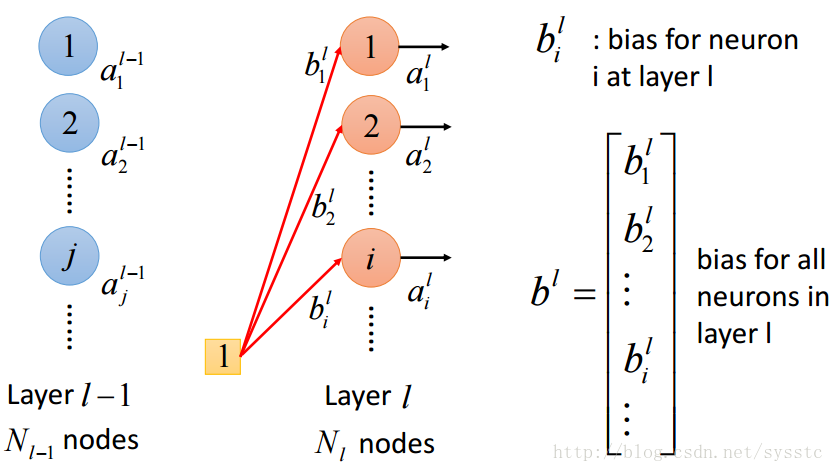
- 偏差:
不同神經元可能會有不同偏差:
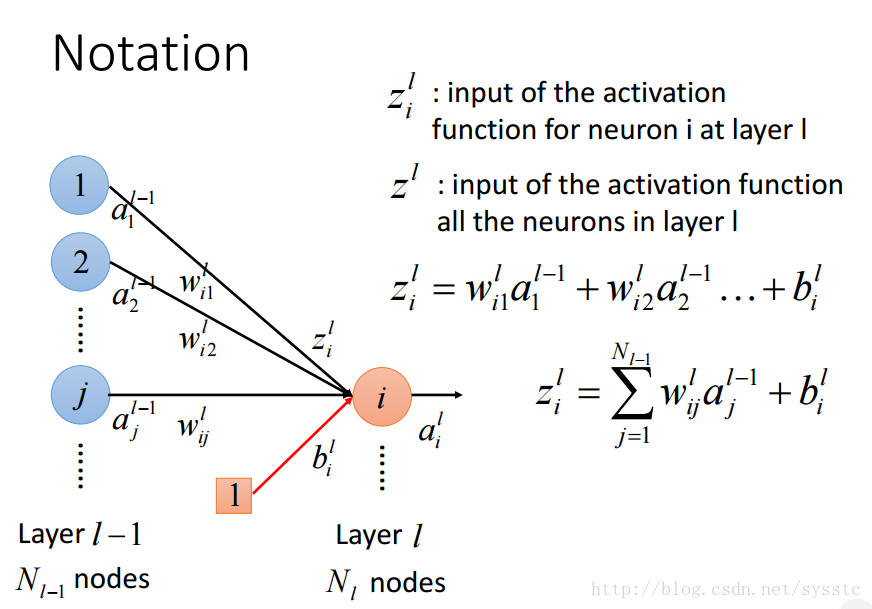
- 啟用函式的輸入z:
- 概念總結:
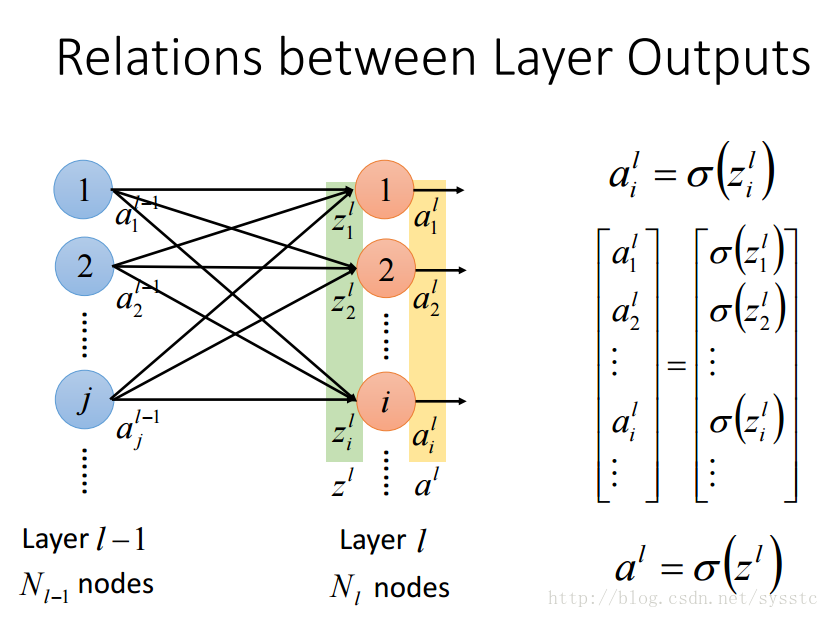
- 啟用函式的輸出a:
- Neural Network就像是一個模型,如下圖所示,是一個全連線前向傳播網路,深度神經網路就是有好多隱藏層。
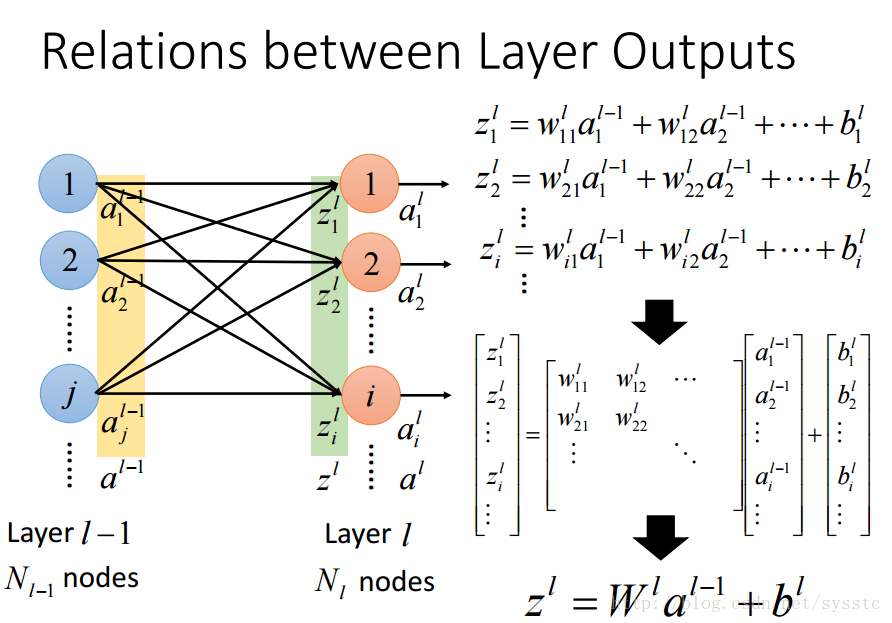
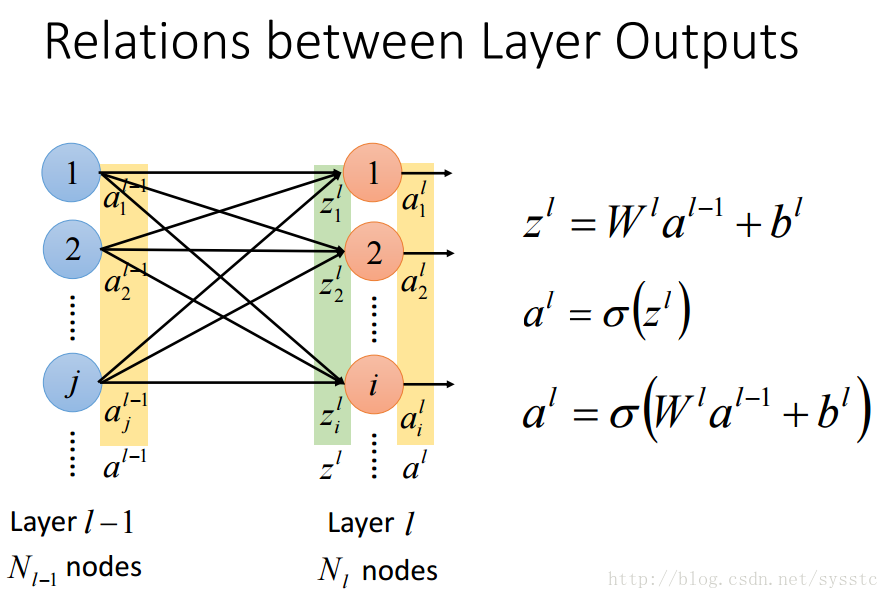
- 層輸出之間的關係:
判斷方法優劣(Cost Function)
- Best Function = Best Parameters
- Parameter指的就是權重W和偏差b,不同的偏差和權重會得到不同的function。我們用θ表示引數集:
- 我們通過Cost Function來判斷方法優劣,C(θ)也叫成本函式/損失函式/誤差函式。
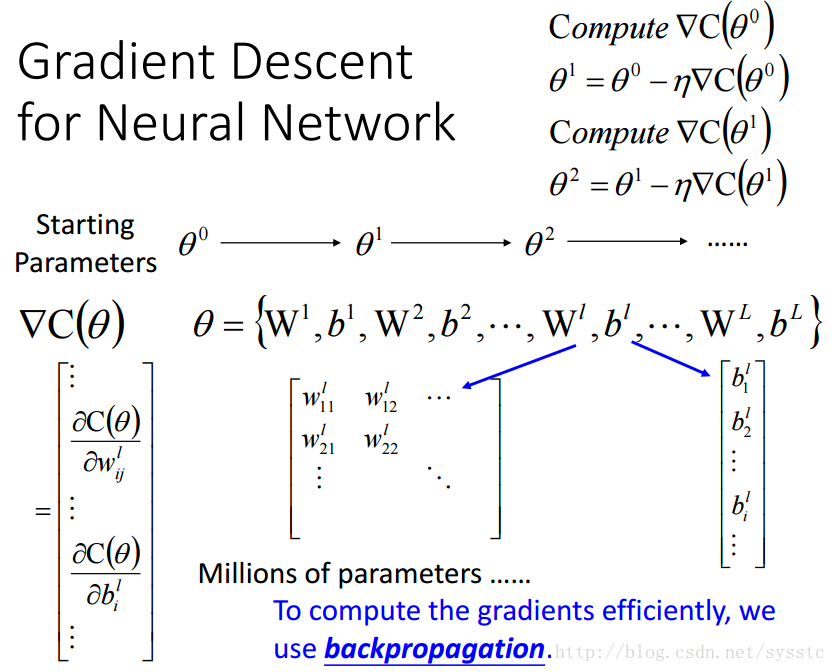
挑選最佳的方法(Gradient Descent)
- 問題描述:
- 函式C(θ):
- θ={θ1,θ2,…},不同的θ表示不同的引數集
- 我們令θ*為最好的引數集。
- 函式C(θ):
- 求解方法:讓C(θ)對θ求偏導,並使其等於0。
- Gradient Descent:
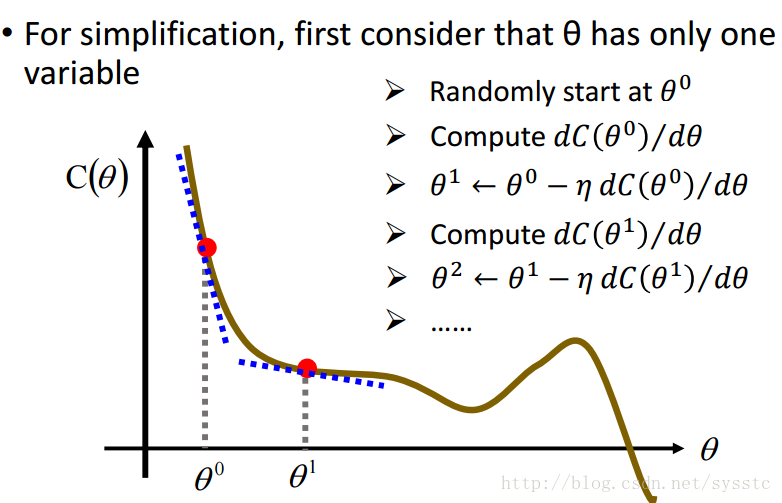
- 做法:
- 起始點為θ0,計算C(θ)在θ0這一點的偏導
- 求出θ1,θ1 = θ0 - learning_rate * [C(θ)在θ0處的偏導]
- 以此類推
- 舉例:
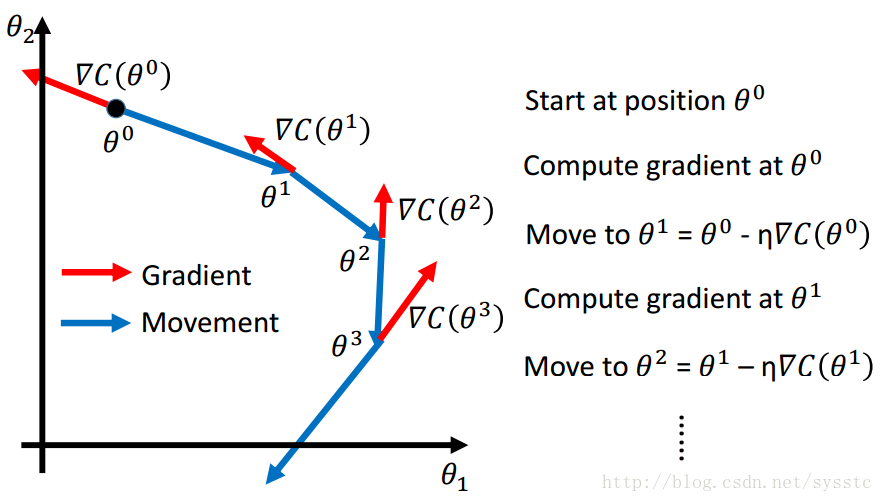
小球滑下的方向就是梯度的反方向,而梯度的反方向就是我們要移動的方向:
- 梯度下降的推導過程:
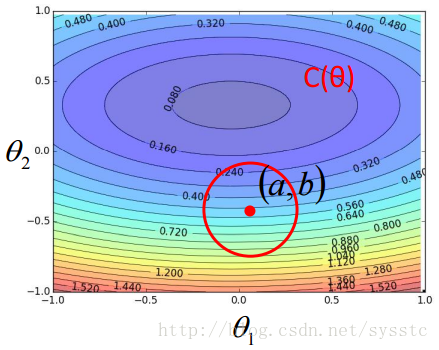
- 泰勒公式(Taylor Series):
因此只要下圖上的紅圈圈足夠小,就能滿足下面式子:
用s代替C(a,b),u 代替C(a,b)對θ1求偏導,v代替C(a,b)對θ2求偏導,因此:
C(θ) = s + u(θ1 - a) + v(θ2 - b) - 梯度下降的更新過程:θ1和θ2是C(θ)在紅圈圈裡的最小值,根據上面推匯出來的公式,我們就可以求出θ1和θ2的值如下:
對於神經網路的梯度下降演算法,我們可以看到C(θ)對θ求偏導就是對權重和偏差求偏導,由於引數很多,因此我們可以使用backpropagation(反向傳播演算法)
- 泰勒公式(Taylor Series):
- 做法:
- 可能遇到的問題:local minima(區域性最優)與saddle point(鞍點)
例項:
- 步驟:
- 引數初始化
- Learning Rate
- 隨機梯度下降(SGD)與Mini-batch
- Recipe for Learning
- 引數初始化θ0:
- 建議:
- 不要將所有引數的值都設成一樣的
- 隨機設定θ0。
- 建議:
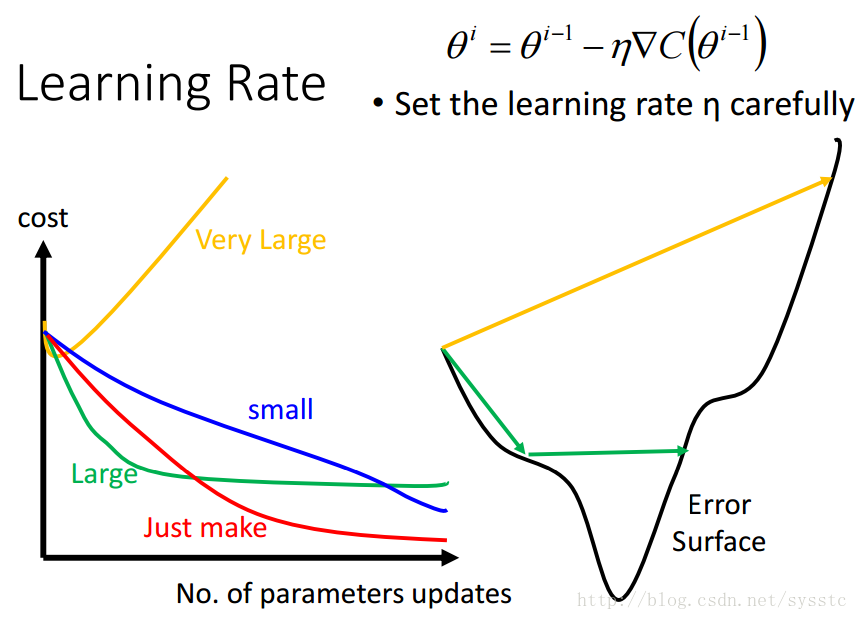
學習率:
- 學習率不能設定的太大,也不能設定的太小:
太小可能會導致效率過慢,要更新很多次才能找到minima;太大可能會導致震盪,也就是形成鋸齒狀。
- 學習率不能設定的太大,也不能設定的太小:
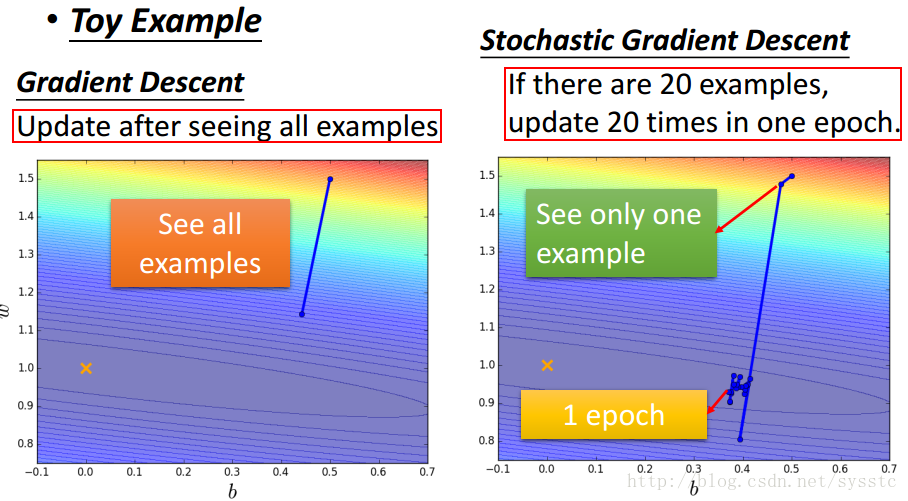
SGD與Mini-batch GD:
- SGD:訓練過程如下:
- GD和SGD的區別:GD每次迭代都要用到全部的訓練資料。SGD每次迭代只用到一個訓練資料來更新引數。
當訓練資料過大時,用GD可能造成記憶體不夠用,那麼就可以用SGD了,SGD其實可以算作是一種online-learning。另外SGD收斂會比GD快,但是對於代價函式求最小值還是GD做的比較好,不過SGD也夠用了。 - Mini-batch Gradient Descent:Mini-batch Gradient Descent就是將training data中batch-size條資料做為一個batch B(記得要亂序shuffle your data),訓練完這個batch B後取batch B中梯度的平均值作為更新梯度的值。
- Mini-batch GD、GD和SGD的區別如下:
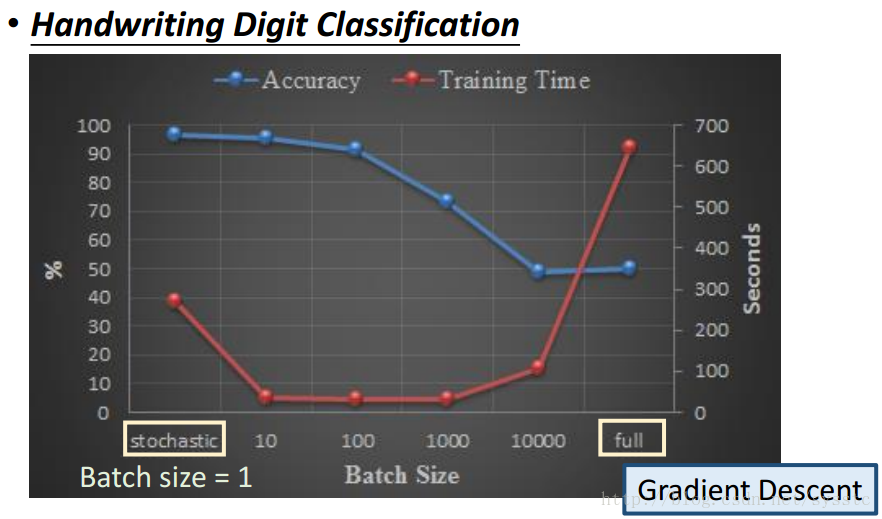
下圖是一個手寫數字識別的例子,在這例子中,橫座標代表的是BatchSize(也就是更新一次用的training data的數量,當batch size = 1時表示的就是SGD,batch size=full時表示的就是GD)
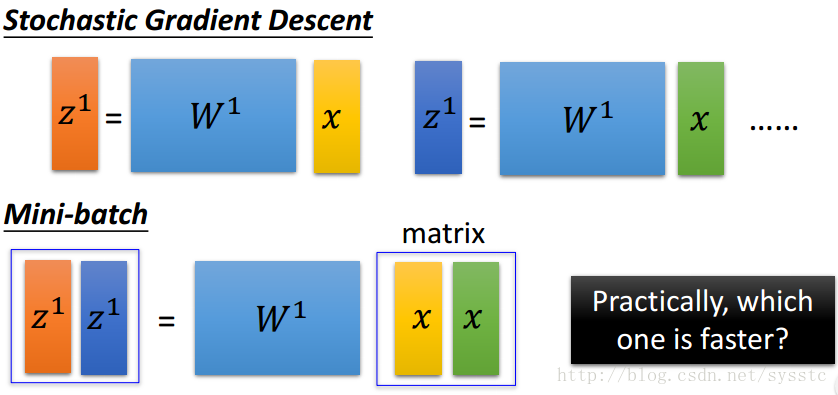
可以看到收斂速度上:Mini-batch>SGD>GD,原因如下:sgd是一個vector x乘以一個權重矩陣W得到vector z;而Mini-batch是一個matrix x(也就是batch-size的x vector的總和)乘以一個權重W,得到一個matrix z。從速度上來說sgd是要快於Mini-batch的。
- SGD:訓練過程如下:
- Recipe for Learning:
- 是否又在Training set中得到好的結果:
- 程式有bug
- 沒有找到good function
- 比如遇到了local minima或saddle point
- 這時候就需要修改training strategy,比如修改learning rate或者是batch-size
- Bad model:如:沒有hidden layer或者是neural不夠多。
- 如果在training data中表現很好,testing data上表現不好,那你可能是overfitting(過擬合)。
- overfitting的來源:
- 因為我們是在training data中找最好的引數,所以testing data中不一定能找到一個好的function。
- 解決overfitting,萬靈丹就是增加training data。
- overfitting的來源:
- 是否又在Training set中得到好的結果:
- 步驟: