協同過濾推薦演算法詳解
一、什麼是協同過濾?
協同過濾是利用集體智慧的一個典型方法。要理解什麼是協同過濾 (Collaborative Filtering, 簡稱 CF),首先想一個簡單的問題,如果你現在想看個電影,但你不知道具體看哪部,你會怎麼做?大部分的人會問問周圍的朋友,看看最近有什麼好看的電影推薦,而我們一般更傾向於從口味比較類似的朋友那裡得到推薦。這就是協同過濾的核心思想。
協同過濾一般是在海量的使用者中發掘出一小部分和你品位比較類似的,在協同過濾中,這些使用者成為鄰居,然後根據他們喜歡的其他東西組織成一個排序的目錄作為推薦給你。當然其中有一個核心的問題:
- 如何確定一個使用者是不是和你有相似的品位?
- 如何將鄰居們的喜好組織成一個排序的目錄?
協同過濾相對於集體智慧而言,它從一定程度上保留了個體的特徵,就是你的品位偏好,所以它更多可以作為個性化推薦的演算法思想。可以想象,這種推薦策略在 Web 2.0 的長尾中是很重要的,將大眾流行的東西推薦給長尾中的人怎麼可能得到好的效果,這也回到推薦系統的一個核心問題:瞭解你的使用者,然後才能給出更好的推薦。
協同過濾推薦演算法是誕生最早,並且較為著名的推薦演算法。主要的功能是預測和推薦。演算法通過對使用者歷史行為資料的挖掘發現使用者的偏好,基於不同的偏好對使用者進行群組劃分並推薦品味相似的商品。協同過濾推薦演算法分為兩類,分別是基於使用者的協同過濾演算法(user-based collaboratIve filtering),和基於物品的協同過濾演算法(item-based collaborative filtering)。簡單的說就是:人以類聚,物以群分。
二、協同過濾的基本流程
首先,要實現協同過濾,需要以下幾個步驟
- 收集使用者偏好
- 找到相似的使用者或物品
- 計算推薦
1、收集使用者偏好
要從使用者的行為和偏好中發現規律,並基於此給予推薦,如何收集使用者的偏好資訊成為系統推薦效果最基礎的決定因素。使用者有很多方式向系統提供自己的偏好資訊,而且不同的應用也可能大不相同,下面舉例進行介紹:

以上列舉的使用者行為都是比較通用的,推薦引擎設計人員可以根據自己應用的特點新增特殊的使用者行為,並用他們表示使用者對物品的喜好。在一般應用中,我們提取的使用者行為一般都多於一種,關於如何組合這些不同的使用者行為,基本上有以下兩種方式:
-
將不同的行為分組 一般可以分為“檢視”和“購買”等等,然後基於不同的行為,計算不同的使用者 / 物品相似度。類似於噹噹網或者 Amazon 給出的“購買了該圖書的人還購買了 ...”,“查看了圖書的人還查看了 ...”
-
加權操作 根據不同行為反映使用者喜好的程度將它們進行加權,得到使用者對於物品的總體喜好。一般來說,顯式的使用者反饋比隱式的權值大,但比較稀疏,畢竟進行顯示反饋的使用者是少數;同時相對於“檢視”,“購買”行為反映使用者喜好的程度更大,但這也因應用而異。
收集了使用者行為資料,我們還需要對資料進行一定的預處理,其中最核心的工作就是:減噪和歸一化。
-
減噪 使用者行為資料是使用者在使用應用過程中產生的,它可能存在大量的噪音和使用者的誤操作,我們可以通過經典的資料探勘演算法過濾掉行為資料中的噪音,這樣可以是我們的分析更加精確。
-
歸一化 如前面講到的,在計算使用者對物品的喜好程度時,可能需要對不同的行為資料進行加權。但可以想象,不同行為的資料取值可能相差很大,比如,使用者的檢視資料必然比購買資料大的多,如何將各個行為的資料統一在一個相同的取值範圍中,從而使得加權求和得到的總體喜好更加精確,就需要我們進行歸一化處理。最簡單的歸一化處理,就是將各類資料除以此類中的最大值,以保證歸一化後的資料取值在 [0,1] 範圍中。
進行的預處理後,根據不同應用的行為分析方法,可以選擇分組或者加權處理,之後我們可以得到一個使用者偏好的二維矩陣,一維是使用者列表,另一維是物品列表,值是使用者對物品的偏好,一般是 [0,1] 或者 [-1, 1] 的浮點數值。
2、找到相似的使用者或物品
當已經對使用者行為進行分析得到使用者喜好後,我們可以根據使用者喜好計算相似使用者和物品,然後基於相似使用者或者物品進行推薦,這就是最典型的 CF 的兩個分支:基於使用者的 CF 和基於物品的 CF。這兩種方法都需要計算相似度,下面我們先看看最基本的幾種計算相似度的方法。 (1)、相似度的計算 關於相似度的計算,現有的幾種基本方法都是基於向量(Vector)的,其實也就是計算兩個向量的距離,距離越近相似度越大。在推薦的場景中,在使用者 - 物品偏好的二維矩陣中,我們可以將一個使用者對所有物品的偏好作為一個向量來計算使用者之間的相似度,或者將所有使用者對某個物品的偏好作為一個向量來計算物品之間的相似度。下面我們詳細介紹幾種常用的相似度計算方法:
- 歐幾里德距離(Euclidean Distance)
最初用於計算歐幾里德空間中兩個點的距離,假設 x,y 是 n 維空間的兩個點,它們之間的歐幾里德距離是:  可以看出,當 n=2 時,歐幾里德距離就是平面上兩個點的距離。
當用歐幾里德距離表示相似度,一般採用以下公式進行轉換:距離越小,相似度越大。
可以看出,當 n=2 時,歐幾里德距離就是平面上兩個點的距離。
當用歐幾里德距離表示相似度,一般採用以下公式進行轉換:距離越小,相似度越大。 
- 皮爾遜相關係數(Pearson Correlation Coefficient)
皮爾遜相關係數一般用於計算兩個定距變數間聯絡的緊密程度,它的取值在 [-1,+1] 之間。  sx, sy是 x 和 y 的樣品標準偏差。
sx, sy是 x 和 y 的樣品標準偏差。
- Cosine 相似度(Cosine Similarity)
Cosine 相似度被廣泛應用於計算文件資料的相似度:  Tanimoto 係數(Tanimoto Coefficient)
Tanimoto 係數(Tanimoto Coefficient)
- Tanimoto 係數
也稱為 Jaccard 係數,是 Cosine 相似度的擴充套件,也多用於計算文件資料的相似度: 
2、相似鄰居的計算
介紹完相似度的計算方法,下面我們看看如何根據相似度找到使用者 - 物品的鄰居,常用的挑選鄰居的原則可以分為兩類:圖 1 給出了二維平面空間上點集的示意圖。 
- 固定數量的鄰居:K-neighborhoods 或者 Fix-size neighborhoods
不論鄰居的“遠近”,只取最近的 K 個,作為其鄰居。如圖 1 中的 A,假設要計算點 1 的 5- 鄰居,那麼根據點之間的距離,我們取最近的 5 個點,分別是點 2,點 3,點 4,點 7 和點 5。但很明顯我們可以看出,這種方法對於孤立點的計算效果不好,因為要取固定個數的鄰居,當它附近沒有足夠多比較相似的點,就被迫取一些不太相似的點作為鄰居,這樣就影響了鄰居相似的程度,比如圖 1 中,點 1 和點 5 其實並不是很相似。
- 基於相似度門檻的鄰居:Threshold-based neighborhoods
與計算固定數量的鄰居的原則不同,基於相似度門檻的鄰居計算是對鄰居的遠近進行最大值的限制,落在以當前點為中心,距離為 K 的區域中的所有點都作為當前點的鄰居,這種方法計算得到的鄰居個數不確定,但相似度不會出現較大的誤差。如圖 1 中的 B,從點 1 出發,計算相似度在 K 內的鄰居,得到點 2,點 3,點 4 和點 7,這種方法計算出的鄰居的相似度程度比前一種優,尤其是對孤立點的處理。
3、計算推薦
經過前期的計算已經得到了相鄰使用者和相鄰物品,下面介紹如何基於這些資訊為使用者進行推薦。
- 基於使用者的 CF(User CF)
基於使用者的 CF 的基本思想相當簡單,基於使用者對物品的偏好找到相鄰鄰居使用者,然後將鄰居使用者喜歡的推薦給當前使用者。計算上,就是將一個使用者對所有物品的偏好作為一個向量來計算使用者之間的相似度,找到 K 鄰居後,根據鄰居的相似度權重以及他們對物品的偏好,預測當前使用者沒有偏好的未涉及物品,計算得到一個排序的物品列表作為推薦。圖 2 給出了一個例子,對於使用者 A,根據使用者的歷史偏好,這裡只計算得到一個鄰居 - 使用者 C,然後將使用者 C 喜歡的物品 D推薦給使用者 A。
- 基於物品的 CF(Item CF)
基於物品的 CF 的原理和基於使用者的 CF 類似,只是在計算鄰居時採用物品本身,而不是從使用者的角度,即基於使用者對物品的偏好找到相似的物品,然後根據使用者的歷史偏好,推薦相似的物品給他。從計算的角度看,就是將所有使用者對某個物品的偏好作為一個向量來計算物品之間的相似度,得到物品的相似物品後,根據使用者歷史的偏好預測當前使用者還沒有表示偏好的物品,計算得到一個排序的物品列表作為推薦。圖 3 給出了一個例子,對於物品 A,根據所有使用者的歷史偏好,喜歡物品 A 的使用者都喜歡物品 C,得出物品 A 和物品 C 比較相似,而使用者 C 喜歡物品 A,那麼可以推斷出使用者 C 可能也喜歡物品 C。

4、兩種演算法的比較
前面介紹了 User CF 和 Item CF 的基本原理,下面我們分幾個不同的角度深入看看它們各自的優缺點和適用場景:
- 計算複雜度
Item CF 和 User CF 是基於協同過濾推薦的兩個最基本的演算法,User CF 是很早以前就提出來了,Item CF 是從 Amazon 的論文和專利發表之後(2001 年左右)開始流行,大家都覺得 Item CF 從效能和複雜度上比 User CF 更優,其中的一個主要原因就是對於一個線上網站,使用者的數量往往大大超過物品的數量,同時物品的資料相對穩定,因此計算物品的相似度不但計算量較小,同時也不必頻繁更新。但我們往往忽略了這種情況只適應於提供商品的電子商務網站,對於新聞,部落格或者微內容的推薦系統,情況往往是相反的,物品的數量是海量的,同時也是更新頻繁的,所以單從複雜度的角度,這兩個演算法在不同的系統中各有優勢,推薦引擎的設計者需要根據自己應用的特點選擇更加合適的演算法。
- 適用場景
在非社交網路的網站中,內容內在的聯絡是很重要的推薦原則,它比基於相似使用者的推薦原則更加有效。比如在購書網站上,當你看一本書的時候,推薦引擎會給你推薦相關的書籍,這個推薦的重要性遠遠超過了網站首頁對該使用者的綜合推薦。可以看到,在這種情況下,Item CF 的推薦成為了引導使用者瀏覽的重要手段。同時 Item CF 便於為推薦做出解釋,在一個非社交網路的網站中,給某個使用者推薦一本書,同時給出的解釋是某某和你有相似興趣的人也看了這本書,這很難讓使用者信服,因為使用者可能根本不認識那個人;但如果解釋說是因為這本書和你以前看的某本書相似,使用者可能就覺得合理而採納了此推薦。相反的,在現今很流行的社交網路站點中,User CF 是一個更不錯的選擇,User CF 加上社會網路資訊,可以增加使用者對推薦解釋的信服程度。
- 推薦多樣性和精度
研究推薦引擎的學者們在相同的資料集合上分別用 User CF 和 Item CF 計算推薦結果,發現推薦列表中,只有 50% 是一樣的,還有 50% 完全不同。但是這兩個演算法確有相似的精度,所以可以說,這兩個演算法是很互補的。 關於推薦的多樣性,有兩種度量方法: 第一種度量方法是從單個使用者的角度度量,就是說給定一個使用者,檢視系統給出的推薦列表是否多樣,也就是要比較推薦列表中的物品之間兩兩的相似度,不難想到,對這種度量方法,Item CF 的多樣性顯然不如 User CF 的好,因為 Item CF 的推薦就是和以前看的東西最相似的。 第二種度量方法是考慮系統的多樣性,也被稱為覆蓋率 (Coverage),它是指一個推薦系統是否能夠提供給所有使用者豐富的選擇。在這種指標下,Item CF 的多樣性要遠遠好於 User CF, 因為 User CF 總是傾向於推薦熱門的,從另一個側面看,也就是說,Item CF 的推薦有很好的新穎性,很擅長推薦長尾裡的物品。所以,儘管大多數情況,Item CF 的精度略小於 User CF, 但如果考慮多樣性,Item CF 卻比 User CF 好很多。 如果你對推薦的多樣性還心存疑惑,那麼下面我們再舉個例項看看 User CF 和 Item CF 的多樣性到底有什麼差別。首先,假設每個使用者興趣愛好都是廣泛的,喜歡好幾個領域的東西,不過每個使用者肯定也有一個主要的領域,對這個領域會比其他領域更加關心。給定一個使用者,假設他喜歡 3 個領域 A,B,C,A 是他喜歡的主要領域,這個時候我們來看 User CF 和 Item CF 傾向於做出什麼推薦:如果用 User CF, 它會將 A,B,C 三個領域中比較熱門的東西推薦給使用者;而如果用 ItemCF,它會基本上只推薦 A 領域的東西給使用者。所以我們看到因為 User CF 只推薦熱門的,所以它在推薦長尾裡專案方面的能力不足;而 Item CF 只推薦 A 領域給使用者,這樣他有限的推薦列表中就可能包含了一定數量的不熱門的長尾物品,同時 Item CF 的推薦對這個使用者而言,顯然多樣性不足。但是對整個系統而言,因為不同的使用者的主要興趣點不同,所以系統的覆蓋率會比較好。
- 總結
從上面的分析,可以很清晰的看到,這兩種推薦都有其合理性,但都不是最好的選擇,因此他們的精度也會有損失。其實對這類系統的最好選擇是,如果系統給這個使用者推薦 30 個物品,既不是每個領域挑選 10 個最熱門的給他,也不是推薦 30 個 A 領域的給他,而是比如推薦 15 個 A 領域的給他,剩下的 15 個從 B,C 中選擇。所以結合 User CF 和 Item CF 是最優的選擇,結合的基本原則就是當採用 Item CF 導致系統對個人推薦的多樣性不足時,我們通過加入 User CF 增加個人推薦的多樣性,從而提高精度,而當因為採用 User CF 而使系統的整體多樣性不足時,我們可以通過加入 Item CF 增加整體的多樣性,同樣同樣可以提高推薦的精度。
- 使用者對推薦演算法的適應度
前面我們大部分都是從推薦引擎的角度考慮哪個演算法更優,但其實我們更多的應該考慮作為推薦引擎的最終使用者 -- 應用使用者對推薦演算法的適應度。 對於 User CF,推薦的原則是假設使用者會喜歡那些和他有相同喜好的使用者喜歡的東西,但如果一個使用者沒有相同喜好的朋友,那 User CF 的演算法的效果就會很差,所以一個使用者對的 CF 演算法的適應度是和他有多少共同喜好使用者成正比的。 Item CF 演算法也有一個基本假設,就是使用者會喜歡和他以前喜歡的東西相似的東西,那麼我們可以計算一個使用者喜歡的物品的自相似度。一個使用者喜歡物品的自相似度大,就說明他喜歡的東西都是比較相似的,也就是說他比較符合 Item CF 方法的基本假設,那麼他對 Item CF 的適應度自然比較好;反之,如果自相似度小,就說明這個使用者的喜好習慣並不滿足 Item CF 方法的基本假設,那麼對於這種使用者,用 Item CF 方法做出好的推薦的可能性非常低。
四、例項演示
1、基於使用者的協同過濾演算法
基於使用者的協同過濾演算法是通過使用者的歷史行為資料發現使用者對商品或內容的喜歡(如商品購買,收藏,內容評論或分享),並對這些喜好進行度量和打分。根據不同使用者對相同商品或內容的態度和偏好程度計算使用者之間的關係。在有相同喜好的使用者間進行商品推薦。簡單的說就是如果A,B兩個使用者都購買了x,y,z三本圖書,並且給出了5星的好評。那麼A和B就屬於同一類使用者。可以將A看過的圖書w也推薦給使用者B。
- 尋找偏好相似的使用者
我們模擬了5個使用者對兩件商品的評分,來說明如何通過使用者對不同商品的態度和偏好尋找相似的使用者。在示例中,5個使用者分別對兩件商品進行了評分。這裡的分值可能表示真實的購買,也可以是使用者對商品不同行為的量化指標。例如,瀏覽商品的次數,向朋友推薦商品,收藏,分享,或評論等等。這些行為都可以表示使用者對商品的態度和偏好程度。

從表格中很難直觀發現5個使用者間的聯絡,我們將5個使用者對兩件商品的評分用散點圖表示出來後,使用者間的關係就很容易發現了。在散點圖中,Y軸是商品1的評分,X軸是商品2的評分,通過使用者的分佈情況可以發現,A,C,D三個使用者距離較近。使用者A(3.3 6.5)和使用者C(3.6 6.3),使用者D(3.4 5.8)對兩件商品的評分較為接近。而使用者E和使用者B則形成了另一個群體。

散點圖雖然直觀,但無法投入實際的應用,也不能準確的度量使用者間的關係。因此我們需要通過數字對使用者的關係進行準確的度量,並依據這些關係完成商品的推薦。
- 歐幾里德距離評價
歐幾里德距離評價是一個較為簡單的使用者關係評價方法。原理是通過計算兩個使用者在散點圖中的距離來判斷不同的使用者是否有相同的偏好。公式參考上面的介紹。 通過公式我們獲得了5個使用者相互間的歐幾里德係數,也就是使用者間的距離。係數越小表示兩個使用者間的距離越近,偏好也越是接近。不過這裡有個問題,太小的數值可能無法準確的表現出不同使用者間距離的差異,因此我們對求得的係數取倒數,使使用者間的距離約接近,數值越大。在下面的表格中,可以發現,使用者A&C使用者A&D和使用者C&D距離較近。同時使用者B&E的距離也較為接近。與我們前面在散點圖中看到的情況一致。

- 皮爾遜相關度評價
皮爾遜相關度評價是另一種計算使用者間關係的方法。他比歐幾里德距離評價的計算要複雜一些,但對於評分資料不規範時皮爾遜相關度評價能夠給出更好的結果。以下是一個多使用者對多個商品進行評分的示例。這個示例比之前的兩個商品的情況要複雜一些,但也更接近真實的情況。我們通過皮爾遜相關度評價對使用者進行分組,並推薦商品。
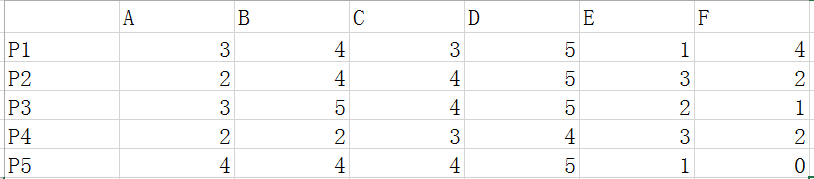
這裡我們使用使用者評分資料如下:其中P1-P5表示五個使用者,A-F表示六個商品。
- 皮爾遜相關係數
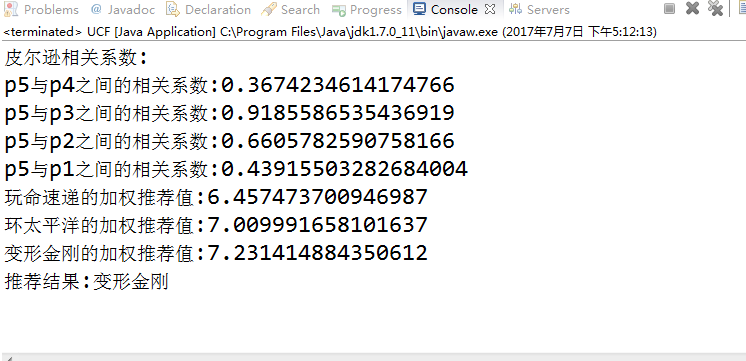
皮爾遜相關係數的計算公式參考上面介紹,結果是一個在-1與1之間的係數。該係數用來說明兩個使用者間聯絡的強弱程度。 假如我們需要給P5使用者推薦東西,那麼我們需要計算P5和P1-4的皮爾遜相關係數。計算結果如下:
- p5與p4之間的相關係數:0.3674234614174766
- p5與p3之間的相關係數:0.9185586535436919
- p5與p2之間的相關係數:0.6605782590758166
- p5與p1之間的相關係數:0.43915503282684004
- 為相似的使用者提供推薦物品
目前我們得到的資料情況如下:我們需要為P5推薦三部電影中的一部,有直接推薦和加權排序推薦兩種方法。
直接推薦:假如我們需要為使用者P5推薦電影,首先我們檢查相似度列表,發現使用者P5和使用者P3的相似度最高。因此,我們可以對使用者P5推薦P3的相關資料。但這裡有一個問題。我們不能直接推薦前面A-F的商品。因為這這些商品使用者P5已經瀏覽或者購買過了。不能重複推薦。因此我們要推薦使用者P5還沒有瀏覽或購買過的商品。如果直接推薦我們可以選擇P3使用者評價最高的商品,也就是環太平洋和變形金剛兩個資料。
加權排序推薦:我們根據不同使用者間的相似度,對不同商品的評分進行相似度加權。按加權後的結果對商品進行排序,然後推薦給使用者P5。這樣,使用者P5就獲得了更好的推薦結果。
上面的計算結果中,我們按照(變形金剛--環太平洋--玩命速遞)的順序把結果推薦給使用者P5。
以上是基於使用者的協同過濾演算法。這個演算法依靠使用者的歷史行為資料來計算相關度。也就是說必須要有一定的資料積累(冷啟動問題)。對於新網站或資料量較少的網站,還有一種方法是基於物品的協同過濾演算法。
下面給出該演算法的Java描述:
- package com.kang;
- import java.util.ArrayList;
- import java.util.Collections;
- import java.util.Comparator;
- import java.util.HashMap;
- import java.util.List;
- import java.util.Map;
- import java.util.Map.Entry;
- //基於使用者的協同過濾演算法
- public class UCF {
- public static void main(String[] args) {
- Map<String, Map<String, Integer>> userPerfMap = new HashMap<String, Map<String, Integer>>();
- Map<String, Integer> pref1 = new HashMap<String, Integer>();
- pref1.put("A", 3);
- pref1.put("B", 4);
- pref1.put("C", 3);
- pref1.put("D", 5);
- pref1.put("E", 1);
- pref1.put("F", 4);
- userPerfMap.put("p1", pref1);
- Map<String, Integer> pref2 = new HashMap<String, Integer>();
- pref2.put("A", 2);
- pref2.put("B", 4);
- pref2.put("C", 4);
- pref2.put("D", 5);
- pref2.put("E", 3);
- pref2.put("F", 2);
- userPerfMap.put("p2", pref2);
- Map<String, Integer> pref3 = new HashMap<String, Integer>();
- pref3.put("A", 3);
- pref3.put("B", 5);
- pref3.put("C", 4);
- pref3.put("D", 5);
- pref3.put("E", 2);
- pref3.put("F", 1);
- userPerfMap.put("p3", pref3);
- Map<String, Integer> pref4 = new HashMap<String, Integer>();
- pref4.put("A", 2);
- pref4.put("B", 2);
- pref4.put("C", 3);
- pref4.put("D", 4);
- pref4.put("E", 3);
- pref4.put("F", 2);
- userPerfMap.put("p4", pref4);
- Map<String, Integer> pref5 = new HashMap<String, Integer>();
- pref5.put("A", 4);
- pref5.put("B", 4);
- pref5.put("C", 4);
- pref5.put("D", 5);
- pref5.put("E", 1);
- pref5.put("F", 0);
- userPerfMap.put("p5", pref5);
- Map<String, Double> simUserSimMap = new HashMap<String, Double>();
- System.out.println("皮爾遜相關係數:");
- for (Entry<String, Map<String, Integer>> userPerfEn : userPerfMap.entrySet()) {
- String userName = userPerfEn.getKey();
- if (!"p5".equals(userName)) {
- double sim = getUserSimilar(pref5, userPerfEn.getValue());
- System.out.println("p5與" + userName + "之間的相關係數:" + sim);
- simUserSimMap.put(userName, sim);
- }
- }
- Map<String, Map<String, Integer>> simUserObjMap = new HashMap<String, Map<String, Integer>>();
- Map<String, Integer> pobjMap1 = new HashMap<String, Integer>();
- pobjMap1.put("玩命速遞", 3);
- pobjMap1.put("環太平洋", 4);
- pobjMap1.put("變形金剛", 3);
- simUserObjMap.put("p1", pobjMap1);
- Map<String, Integer> pobjMap2 = new HashMap<String, Integer>();
- pobjMap2.put("玩命速遞", 5);
- pobjMap2.put("環太平洋", 1);
- pobjMap2.put("變形金剛", 2);
- simUserObjMap.put("p2", pobjMap2);
- Map<String, Integer> pobjMap3 = new HashMap<String, Integer>();
- pobjMap3.put("玩命速遞", 2);
- pobjMap3.put("環太平洋", 5);
- pobjMap3.put("變形金剛", 5);
- simUserObjMap.put("p3", pobjMap3);
- System.out.println("推薦結果:" + getRecommend(simUserObjMap, simUserSimMap));
- }
- //Claculate Pearson Correlation Coefficient
- public static double getUserSimilar(Map<String, Integer> pm1, Map<String, Integer> pm2) {
- int n = 0;// 數量n
- int sxy = 0;// Σxy=x1*y1+x2*y2+....xn*yn
- int sx = 0;// Σx=x1+x2+....xn
- int sy = 0;// Σy=y1+y2+...yn
- int sx2 = 0;// Σx2=(x1)2+(x2)2+....(xn)2
- int sy2 = 0;// Σy2=(y1)2+(y2)2+....(yn)2
- for (Entry<String, Integer> pme : pm1.entrySet()) {
- String key = pme.getKey();
- Integer x = pme.getValue();
- Integer y = pm2.get(key);
- if (x != null && y != null) {
- n++;
- sxy += x * y;
- sx += x;
- sy += y;
- sx2 += Math.pow(x, 2);
- sy2 += Math.pow(y, 2);
- }
- }
- // p=(Σxy-Σx*Σy/n)/Math.sqrt((Σx2-(Σx)2/n)(Σy2-(Σy)2/n));
- double sd = sxy - sx * sy / n;
- double sm = Math.sqrt((sx2 - Math.pow(sx, 2) / n) * (sy2 - Math.pow(sy, 2) / n));
- return Math.abs(sm == 0 ? 1 : sd / sm);
- }
- //獲取推薦結果
- public static String getRecommend(Map<String, Map<String, Integer>> simUserObjMap,
- Map<String, Double> simUserSimMap) {
- Map<String, Double> objScoreMap = new HashMap<String, Double>();
- for (Entry<String, Map<String, Integer>> simUserEn : simUserObjMap.entrySet()) {
- String user = simUserEn.getKey();
- double sim = simUserSimMap.get(user);
- for (Entry<String, Integer> simObjEn : simUserEn.getValue().entrySet()) {
- double objScore = sim * simObjEn.getValue();//加權(相似度*評分)
- String objName = simObjEn.getKey();
- if (objScoreMap.get(objName) == null) {
- objScoreMap.put(objName, objScore);
- } else {
- double totalScore = objScoreMap.get(objName);
- objScoreMap.put(objName, totalScore + objScore);//將所有使用者的加權評分作為最後的推薦結果資料
- }
- }
- }
- List<Entry<String, Double>> enList = new ArrayList<Entry<String, Double>>(objScoreMap.entrySet());
- Collections.sort(enList, new Comparator<Map.Entry<String, Double>>() {//排序
- public int compare(Map.Entry<String, Double> o1, Map.Entry<String, Double> o2) {
- Double a = o1.getValue() - o2.getValue();
- if (a == 0) {
- return 0;
- } else if (a > 0) {
- return 1;
- } else {
- return -1;
- }
- }
- });
- for (Entry<String, Double> entry : enList) {
- System.out.println(entry.getKey()+"的加權推薦值:"+entry.getValue());
- }
- return enList.get(enList.size() - 1).getKey();//返回推薦結果
- }
- }
2、基於物品的協同過濾演算法
基於物品的協同過濾演算法與基於使用者的協同過濾演算法很像,將商品和使用者互換。通過計算不同使用者對不同物品的評分獲得物品間的關係。基於物品間的關係對使用者進行相似物品的推薦。這裡的評分代表使用者對商品的態度和偏好。簡單來說就是如果使用者A同時購買了商品1和商品2,那麼說明商品1和商品2的相關度較高。當用戶B也購買了商品1時,可以推斷他也有購買商品2的需求。
- 尋找相似的物品

表格中是兩個使用者對5件商品的評分。在這個表格中我們使用者和商品的位置進行了互換,通過兩個使用者的評分來獲得5件商品之間的相似度情況。單從表格中我們依然很難發現其中的聯絡,因此我們選擇通過散點圖進行展示。

在散點圖中,X軸和Y軸分別是兩個使用者的評分。5件商品按照所獲的評分值分佈在散點圖中。我們可以發現,商品1,3,4在使用者A和B中有著近似的評分,說明這三件商品的相關度較高。而商品5和2則在另一個群體中。
- 歐幾里德距離評價
在基於物品的協同過濾演算法中,我們依然可以使用歐幾里德距離評價來計算不同商品間的距離和關係。 通過歐幾里德係數可以發現,商品間的距離和關係與前面散點圖中的表現一致,商品1,3,4距離較近關係密切。商品2和商品5距離較近。

- 皮爾遜相關度評價
我們選擇使用皮爾遜相關度評價來計算多使用者與多商品的關係計算。下面是5個使用者對5件商品的評分表。我們通過這些評分計算出商品間的相關度。

- 皮爾遜相關度計算公式
通過計算可以發現,商品1&2,商品3&4,商品3&5和商品4&5相似度較高。下一步我們可以依據這些商品間的相關度對使用者進行商品推薦。

- 為使用者提供基於相似物品的推薦
這裡我們遇到了和基於使用者進行商品推薦相同的問題,當需要對使用者3基於商品3推薦商品時,需要一張新的商品與已有商品間的相似度列表。在前面的相似度計算中,商品3與商品4和商品5相似度較高,因此我們計算並獲得了商品4,5與其他商品的相似度列表。

以下是通過計算獲得的新商品與已有商品間的相似度資料。

- 加權排序推薦
這裡是使用者3已經購買過的商品4,5與新商品A,B,C直接的相似程度。我們將使用者3對商品4,5的評分作為權重。對商品A,B,C進行加權排序。使用者3評分較高並且與之相似度較高的商品被優先推薦。

經過以上分析,我們按照(C-B-A)的順序推薦商品給使用者。
下面給出使用MapReduce實現的基本思路。
資料集欄位:
- User_id: 使用者ID
- Item_id: 物品ID
- preference:使用者對該物品的評分
演算法的思想:
- 1、建立物品的同現矩陣A,即統計兩兩物品同時出現的次數
- 資料格式:Item_id1:Item_id2 次數
- 2、 建立使用者對物品的評分矩陣B,即每一個使用者對某一物品的評分
- 資料格式:Item_id user_id:preference
- 3、 推薦結果=物品的同現矩陣A * 使用者對物品的評分矩陣B
- 資料格式:user_id item_id,推薦分值
- 4、 過濾使用者已評分的物品項
- 5.、對推薦結果按推薦分值從高到低排序
- 1,101,5.0
- 1,102,3.0
- 1,103,2.5
- 2,101,2.0
- 2,102,2.5
- 2,103,5.0
- 2,104,2.0
- 3,101,2.0
- 3,104,4.0
- 3,105,4.5
- 3,107,5.0
- 4,101,5.0
- 4,103,3.0
- 4,104,4.5
- 4,106,4.0
- 5,101,4.0
- 5,102,3.0
- 5,103,2.0
- 5,104,4.0
- 5,105,3.5
- 5,106,4.0
- 6,102,4.0
- 6,103,2.0
- 6,105,3.5
- 6,107,4.0
Hadoop MapReduce程式分為四步: 第一步: 讀取原始資料,按使用者ID分組,輸出檔案資料格式為
- 1 103:2.5,101:5.0,102:3.0
- 2 101:2.0,102:2.5,103:5.0,104:2.0
- 3 107:5.0,101:2.0,104:4.0,105:4.5
- 4 103:3.0,106:4.0,104:4.5,101:5.0
- 5 101:4.0,102:3.0,103:2.0,104:4.0,105:3.5,106:4.0
- 6 102:4.0,103:2.0,105:3.5,107:4.0
第二步:統計兩兩物品同時出現的次數,輸出檔案資料格式為
- 101:101 5
- 101:102 3
- 101:103 4
-
相關推薦
協同過濾推薦演算法詳解
一、什麼是協同過濾?
協同過濾是利用集體智慧的一個典型方法。要理解什麼是協同過濾 (Collaborative Filtering, 簡稱 CF),首先想一個簡單的問題,如果你現在想看個電影,但你不知道具體看哪部,你會怎麼做?大部分的人會問問周圍的朋友,看看最近有什麼好看的電影推薦,而我們一般更傾向於從
基於使用者的協同過濾和基於物品的協同過濾推薦演算法圖解
在協同過濾中,有兩種主流方法:基於使用者的協同過濾,和基於物品的協同過濾。具體怎麼來闡述他們的原理呢,看個圖大家就明白了
基於使用者的 CF 的基本思想相當簡單,基於使用者對物品的偏好找到相鄰鄰居使用者,然後將鄰居使用者喜歡的推薦給當前使用者。計算上,就是將一個使用者對所有物品
基於譜聚類SM演算法的協同過濾推薦演算法研究——清華師兄畢業論文學習
一、個性化推薦演算法
1.相似度的比較
兩個商品或者商品之間相似的的計算方法,量化屬性為非數值型資料的商品或者使用者之間的接近程度。通常我們計算使用者或者專案間相似度的主要方法有餘弦相似度(Cosime Similarity)、Jaccard係數和pearson相關(pearson Corr
使用Python的Pandas庫實現基於使用者的協同過濾推薦演算法
本文在下文的程式碼基礎上修改而來:
環境
版本
Python
3.5.5
Pandas
0.22.0
import pandas as pd
df = None
def dataSet2Matrix(
協同過濾推薦演算法的優化(稀疏矩陣的處理)
簡單的協同過濾演算法流程如下
(1)、計算其他使用者和你的相似度,可以使用反差表忽略一部分使用者
(2)、根據相似度的高低找出K個與你最相似的鄰居
(3)、在這些鄰居喜歡的物品中,根據鄰居與你的遠近程度算出每一件物品的推薦度
(4)、根據每一件物品的推薦度高低給你推薦物品。
推薦演算法概述:基於內容的推薦演算法、協同過濾推薦演算法和基於知識的推薦演算法
所謂推薦演算法就是利用使用者的一些行為,通過一些數學演算法,推測出使用者可能喜歡的東西。推薦演算法主要分為兩種
1. 基於內容的推薦
基於內容的資訊推薦方法的理論依據主要來自於資訊檢索和
協同過濾推薦演算法之Slope One的介紹
Slope One 之一 : 簡單高效的協同過濾演算法(轉)(
原文地址:http://blog.sina.com.cn/s/blog_4d9a06000100am1d.html
現在做的一個專案中需要用到推薦演算法, 在網上查了一下.
Beyo
基於使用者(user-based)的協同過濾推薦演算法的初步理解以及程式碼實現
總論
協同過濾是目前最經典的推薦演算法。
分而理之,協同,指通過線上資料找到使用者可能喜歡的物品;過濾,濾掉一些不值得推薦的資料。
協同過濾推薦分為三種類型。第一種是基於使用者(user-based)的協同過濾,第二種是基於專案(ite
基於使用者的協同過濾推薦演算法原理和實現
在推薦系統眾多方法中,基於使用者的協同過濾推薦演算法是最早誕生的,原理也較為簡單。該演算法1992年提出並用於郵件過濾系統,兩年後1994年被 GroupLens 用於新聞過濾。一直到2000年,該演算法都是推薦系統領域最著名的演算法。 本文簡單介紹基於使用者的協同
基於內容推薦演算法詳解(比較全面的文章)
Collaborative Filtering Recommendations (協同過濾,簡稱CF) 是目前最流行的推薦方法,在研究界和工業界得到大量使用。但是,工業界真正使用的系統一般都不會只有CF推薦演算法,Content-based Recommendations
機器學習演算法(推薦演算法)—協同過濾推薦演算法(2)
一、基於協同過濾的推薦系統
協同過濾(Collaborative Filtering)的推薦系統的原理是通過將使用者和其他使用者的資料進行比對來實現推薦的。比對的具體方法就是通過計算兩個使用者
基於社交網路的使用者與基於物品的協同過濾推薦演算法-java
完整工程+資料來源:https://github.com/scnuxiaotao/recom_sysimport java.io.BufferedReader;
import java.io.FileNotFoundException;
import java.io.Fil
mahout推薦演算法——協同過濾推薦演算法(java程式碼實現)
什麼是協同過濾
協同過濾是利用集體智慧的一個典型方法。要理解什麼是協同過濾 (Collaborative Filtering, 簡稱 CF),首先想一個簡單的問題,如果你現在想看個電影,但你不知道具體看哪部,你會怎麼做?大部分的人會問問周圍的朋友,看看最近有什麼好看的電影推
協同過濾推薦演算法-----向量之間的相似度
Collaborative Filtering Recommendation
度量向量之間的相似度方法很多了,你可以用距離(各種距離)的倒數,向量夾角,Pearson相關係數等。
皮爾森相關係數計算公式如下:
ρX,Y=cov(X,Y)σxσy=E((X−μx)
【推薦】演算法詳解
感覺不錯的一些文章推薦下!!!
並查集詳解 ★★★★★
動態規劃詳解 ★★★★★
位運算藝術(一)
拓撲排序
最小生成樹-Prim演算法和Kruskal演算法
最短路徑——SPFA演算法
最短路演算法
協同過濾推薦之slope one演算法
1.示例引入
比如說你在京東選購手機iphone和note7:
消費者用過後,會有相關的評分。
假設評分如下:
評分 iphone note7
小a 4 5
小b 4 3
小c 2 3
小d 3 ?
問題:請猜測一下小d可能會給“note7”打多少分?
推薦系統基礎演算法--餘弦相似度演算法詳解及應用
一、簡述
這幾天在看《推薦系統實戰》這本書。其中,基於領域的演算法是推薦系統中最基本的演算法,什麼是基於領域的演算法呢?簡單來說就是基於使用者(或物品)的協同過濾演算法,所謂的協同的意思就是需要使用者(或物品)共同參與。從而通過使用者的行為,
基於Spark MLlib平臺和基於模型的協同過濾演算法的電影推薦系統(一) 協同過濾演算法概述&&基於模型的協同過濾的演算法思想(演算法模型和結構待補充)
本文暫時分為三部分:
(一)基於Spark MLlib平臺和基於模型的協同過濾演算法的電影推薦系統(一)
→ 協同過濾演算法概述&&基於模型的協同過濾的演算法思想
(二)基於Spark MLlib平臺和基於模型的協同過濾演算法的電影推薦
差分分組的合作協同進化的大規模優化演算法詳解
合作協同進化已經引入協同進化演算法,目的是通過分而治之的正規化解決日益複雜的優化問題。理論上,協同改 變子成分的想法是十分適合解決大規模優化問題的。然而在實踐中,沒有關於問題的先驗知識, 問題應如何分解是尚不清楚的。在本文中,我們提出一個自動分解策略,稱為差分分
隱性反饋行為數據的協同過濾推薦算法
only 場景 sin blank 沈默 post strong inpu level
隱性反饋行為數據的協同過濾推薦算法
《Collaborative Filtering for Implicit Feedback Datasets》論文筆記
本文是我閱讀《C