題目連結

P4285 [SHOI2008]漢諾塔

解題思路

提供一種打表新思路

先來證明一個其他題解都沒有證明的結論：\(ans[i]\)是可由\(ans[i-1]\)線性遞推的。

（\(ans[i]\)表示\(i\)個盤子全部移走的步數）

感謝keytoyzi神仙的神仙思路

首先，在最初兩層移動的時候，遵循的移動順序規則是題中所給的順序。

在\(n\)個盤子都在\(A\)柱的時候，我們是怎麼做的呢？

先把前\(n-1\)個盤子按照遵循初始順序規則的方法移動到\(B\)或\(C\)；

再對第\(n\)個盤子進行操作；

再進行某些操作（後文會展開）；

最後所有盤子移動到\(B\)

這等價於：

每一層對應一個新規則，把前\(n-1\)層盤子看做一層，那就相當於按照這個新的規則移動一個兩層的東西。

這個新規則是啥意思呢？光說理論太難以理解，上圖：

解釋一下：\(n-1\)代表前\(n-1\)個盤子，這些盤子根據初始規則可能移動到\(B\)或者\(C\)，而把他們看做一個整體後，相當於上圖的遵循初始規則的移動方式，而這種新的移動方式，就是一個新的規則。

再來兩張狀態轉移的圖：

（單箭頭表示這一步操作優先順序高於另一側）

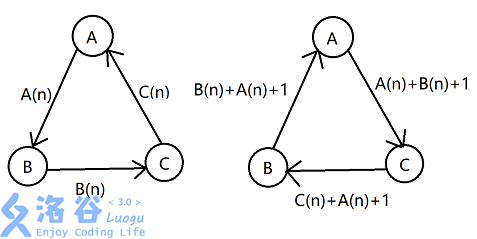
解釋一下這張圖。

剛開始對於前\(n\)個盤子形成的新規則：

\(AB>AC\)，\(BC>BA\)

根據這個規則進行第\(n+1\)層的操作：（以\(A \to C\)為例）

先把\(A\)上的前\(n\)個盤子扔到\(B\)上；（\(A(n)\)）

再把\(A\)最底下的第\(n+1\)個盤子扔到\(C\)上；（\(1\)）

再把扔到\(B\)上的前\(n\)個盤子扔到\(C\)上。（\(B(n)\)）

故總步驟數為\(A(n)+1+B(n)\)。

同理，那麼這就給出了一組遞推關係。

易得，如果\(n\)滿足左圖，則\(n+1\)滿足右圖；

如果\(n\)滿足右圖，則\(n+1\)滿足左圖。

也就是說，這兩張圖中的狀態可以互相轉換。

又，\(ABC\)

這張圖更復雜一些，不過實質和剛剛的相同。

以\(A\to B\)為例。

先把\(A\)上的前\(n\)個盤子扔到\(B\)上；（\(A(n)\)）

再把\(A\)最底下的第\(n+1\)個盤子扔到\(C\)上；（\(1\)）

再把\(A\)上的這n個盤子扔回\(A\)上；（\(B(n)\)）

再把\(C\)上的第n+1個盤子扔到\(B\)上；（\(1\)）

再把\(A\)上的那\(n\)個盤子扔回\(B\)上。（\(B(n)\)）

故總步驟數為\(A(n)+1+B(n)+1+B(n)\)。

同理易得，如果n滿足左圖，則n+1滿足右圖；

如果\(n\)滿足右圖，則\(n+1\)滿足左圖。

也就是說，這兩張圖中的狀態還是可以互相轉換。

而在這張圖上，\(AB\)是等價的，\(C\)是另一種情況，故這張狀態圖對應了兩種可能的答案：

\(AB\)對應的狀態為初始\(A\)柱（答案\(2\)）

或

\(C\)對應的狀態為初始\(A\)柱（答案\(3\)）。

好，那麼現在對應這三種情況做一種簡單的分析。

對於第一種答案：

\(ABC\)等價，故\(A(n)=B(n)=C(n)=ans_1[n]\)

由圖中的遞推公式，\(ans_1[n+1]=ans_1[n]*2+1\)

對於第二種答案：

\(AB\)等價，\(A(n)=B(n)=ans_2[n]\)

\(ans_2[n+1]=ans_2[n]*3+2\)

對於第三種答案：

\(AB\)等價，\(A(n)=B(n)=ans_2[n]\)

\(ans_3[n+1]=ans_2[n]+ans_3[n]+1\)

這是一個線性表示式。

證畢。

所以，我們只需要知道移動一個盤子、兩個盤子、三個盤子的情況，即可知道遞推公式進而求解。

手動模擬打表，容易得到以下結果：

（\(ans[i]\)表示i個盤子全部移走的步數）

一個盤子：

\(ans[1]=1\)

兩個盤子：

\((1)AB>AC\)

①\(BC>BA\)，\(ans[2]=3\)

②\(BC<BA\)，\(ans[2]=5\)

\((2)AB<AC\)

這裡可以看做把\(BC\)柱子換了個位置

①\(ans[2]=3\)：原\(BC>BA\)，把\(BC\)換了個位置後變成\(CB>CA\)

②\(ans[2]=5\)：原\(BC<BA\)，同理變成\(CB<CA\)

三個盤子：

\((1)AB>AC\)

①\(BC>BA\)

\((i)CB>CA\)，\(ans[3]=9\)

\((ii)CB<CA\)，\(ans[3]=7\)

②\(BA>BC\)

\(ans[3]=17\)

\((2)AB<AC\)

同理，不再贅述

下附遞推AC程式碼：

#include<stdio.h>
char a[4];
int seq[3][3];
long long ans[40];
int main(){
    int i,n;
    scanf("%d",&n);
    for(i=0;i<6;i++){
        scanf("%s",a);
        seq[a[0]-'A'][a[1]-'A']=6-i;
    }
    if(seq[0][1]>seq[0][2]){//AB>AC
        if(seq[1][2]<seq[1][0]){//BC<BA
            ans[2]=5;ans[3]=17;
        }else{
            if(seq[2][0]>seq[2][1]){//CA>CB
                ans[2]=3;ans[3]=7;
            }else{
                ans[2]=3;ans[3]=9;
            }
        }
    }else{//AB<AC 
        if(seq[2][1]<seq[2][0]){//CB<CA
            ans[2]=5;ans[3]=17;
        }else{
            if(seq[1][0]>seq[1][2]){//BA>BC
                ans[2]=3;ans[3]=7;
            }else{
                ans[2]=3;ans[3]=9;
            }
        }
    }
    ans[1]=1;
    int b=(ans[2]*ans[2]-ans[1]*ans[3])/(ans[2]-ans[1]);
    int k=(ans[2]-b)/cnt1;
    for(i=4;i<=n;i++)ans[i]=ans[i-1]*k+b;
    printf("%lld",ans[n]);
    return 0;
}

其實，這已經沒有必要寫成遞推形式了。我們在討論三種答案的時候，其實已經可以手算算出三種情況的O(1)表示式了。

來一發最短AC程式碼

#include<stdio.h>
#include<math.h>
typedef long long ll;
char a[4];
int s[9],p,n,i=6;
ll f(int x){
    if(x==1)return (ll)2*pow(3,n-1)-1;
    if(x)return (ll)pow(2,n)-1;
    return (ll)pow(3,n-1);
}
int main(){
    scanf("%d",&n);
    while(i--)scanf("%s",a),s[(a[0]-'A')*3+a[1]-'A']=i;
    if(s[1]>s[2]){
        if(s[5]<s[3])p=1;
        else if(s[6]>s[7])p=2;
    }else if(s[7]<s[6])p=1;
    else if(s[3]>s[5])p=2;
    printf("%lld",f(p));
    return 0;
}