漢諾塔問題(python版)
漢諾塔的移動可以用遞迴函式非常簡單地實現。(此題可以聯絡 棧的反轉 問題)
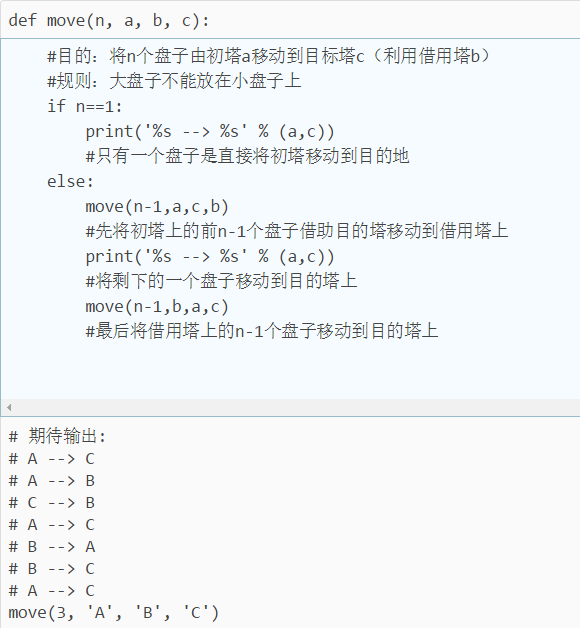
請編寫move(n, a, b, c)函式,它接收引數n,表示3個柱子A、B、C中第1個柱子A的盤子數量,然後打印出把所有盤子從A藉助B移動到C的方法,例如:
演算法:當只有一個盤子的時候,只需要將A塔上的一個盤子移動到C塔上。
當A塔上有2個盤子的時候,先將A塔上的1號盤子(編號從上到下)移動到B塔上,再將A塔的2號盤子移動到C塔上,最後將B塔上的小盤子移動到C塔上。
當A塔上有3個盤子的時候,先將A塔上編號1到2的盤子(共2個)移動到B塔上(需藉助C塔),然後將A塔上最大的n號盤子移動到C盤,最後將B塔上的兩個盤子藉助A塔移動到C塔上。
當A塔上有n個盤子的時候,先將A塔傷編號1-n-1的盤子(共n-1個)移動到B塔上(藉助C塔),然後將A塔傷最大的n號盤子移動到C塔上,最後將B塔上的n-1個盤子藉助A塔移動到C塔上。
綜上,除了只有一個盤子的時候不需要藉助其他塔外,其餘情況可用遞迴解決。
相關推薦
漢諾塔遊戲規律,讓漢諾塔淪為體力勞動!(後附漢諾塔解法Python原始碼)
記住這個規律,以後玩漢諾塔基本上就是體力勞動了。 規律: 先小後大,單左雙右,迴圈。 設3個柱子分別是甲,乙,丙,把3根柱子看成一個迴圈,也就是說,甲的右邊是乙,乙的右邊是丙,而丙的右邊則回到甲,同理,甲的左邊就是丙。簡單點,記住丙的右邊是甲,和甲的左邊是丙就行了。
漢諾塔(遞迴)
閱讀遞迴函式最容易的方法不是糾纏於它的執行過程,而是相信遞迴函式會順利完成它的任務。如果你的每個步驟正確無誤,你的限制條件設定正確,並且每次呼叫之後更接近限制條件,遞迴函式總是能夠正確地完成任務。——《C和指標》 一、遊戲規則 有三個塔,第一個塔上放了若干個盤子。要將這若干個盤子
遞迴的應用——斐波那契數列、漢諾塔(Java實現)
package ch06; public class Fibonacci { public static int getNumber(int n) { if(n == 1) { return 0; } else if(n == 2){
SDUT OJ 1200 漢諾塔(遞迴)
漢諾塔 Problem Description 漢諾塔(又稱河內塔)問題是印度的一個古老的傳說。 開天闢地的神勃拉瑪在一個廟裡留下了三根金剛石的棒A、B和C,A上面套著n個圓的金片,最大的一個在底下,其餘一個比一個小,依次疊上去,廟裡的眾僧不倦地把它們一個個地從A棒搬到C棒上,規定可
BNUOJ 34978 漢諾塔 (概率dp)
pre lin for ron 2.0 pla return popu while 題目分析:對於 i 個盤 , 須要移動多少步,取決於最大的盤子在哪個桿上。在C桿上,則最大的盤不須
漢諾塔問題(python版)
漢諾塔的移動可以用遞迴函式非常簡單地實現。(此題可以聯絡 棧的反轉 問題) 請編寫move(n, a, b, c)函式,它接收引數n,表示3個柱子A、B、C中第1個柱子A的盤子數量,然後打印出把所有盤子從A藉助B移動到C的方法,例如: 演算法:當只有一個盤子的時候
兩個python小練習 (漢諾塔 楊輝三角)
漢諾塔 原理:利用遞迴 1、將前n-1個盤子從A移到B上 2、將最後一個盤子從A移到C上 3、將B的n-1個移到C上 其次數為:1,3,7……即2n+1 python程式碼: def move(n,a,b,c): if n==1: &nb
Python解決漢諾塔(遞迴演算法)
move(1,a,b,c) 把柱子a上最後1個盤子移到柱子c上 move(n-1,b,a,c) 把柱子b上的n-1個盤子通過柱子a移動到柱子c上print move(4, 'A', 'B', 'C')
漢諾塔(河內塔)問題:
漢諾塔 medium 問題 http int logs 一行 移動 else 漢諾塔(又稱河內塔)問題是源於印度一個古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子,在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小
nyoj 1078 漢諾塔(四)[二分圖 || 規律 || 暴力 || 貪心]
二分圖 二分圖匹配 int 處理 names 特殊 mes while 最小路徑覆蓋 題目:nyoj 1078 漢諾塔(四) 分析:做這個題目的時候是在圖論的題目裏面看到的。到時讀了題目推了一下,發現好像有點規律。試了一下果然過了。 後來看了一下數據,才50。那
漢諾塔(三)
++ 但是 logs 大片 scanf pan 兩種 初始 入棧 漢諾塔(三) 描述 在印度,有這麽一個古老的傳說:在世界中心貝拿勒斯(在印度北部)的聖廟裏,一塊黃銅板上插著三根寶石針。印度教的主神梵天在創造世界的時候,在其中一根針上從下到上地穿好了由大到小的64片金片
課後作業——遞歸(組合數、漢諾塔、回文)
bigint 遞歸函數 指定 lang ole 作業1 eof 2-2 image 課後作業1 使用組合數公式利用n!來計算 一、 程序設計思想 定義n,k,輸入並檢測輸入的值是否是整數,如果n>k,調用計算階乘的函數,計算並輸出結果。階乘計算函數使用遞歸的思想,並使
演算法之路(四)----漢諾塔(又稱河內之塔)
漢諾塔是很簡單也很經典的演算法之一。 漢諾塔是根據一個傳說形成的數學問題: 有三根杆子A,B,C 。A杆上有N個(N>1)穿孔圓盤,盤的尺寸由下到上依次變小。要求按下列規則將所有圓盤移至C杆: * 1 每次只能移動一個圓盤; * 2 大盤不能疊在小盤上面。 提示:可將圓
NYOJ 漢諾塔(三)
漢諾塔(三) 時間限制:3000 ms | 記憶體限制:65535 KB 難度:3 描述 在印度,有這麼一個古老的傳說:在世界中心貝拿勒斯(在印度北部)的聖廟裡,一塊黃銅板上插著三根寶石針。印度教的主神梵天在創造世界的時候,在其中一根針上從下到上地穿好了由大到
漢諾塔(hanoi)
漢諾塔程式碼: def hanoi(n,x,y,z): if n == 1: print(x,'-->',z) else: hanoi(n-1,x,z,y) print(x,'-->',z) hanoi(n-1
漢諾塔(內部+偽圖形)
1.1問題描述: 假設有三個分別命名為A,B,C的塔座,在塔座A上插有n個直徑大小各不相同的圓盤,大的在下,小的在上,且從小到大編號為1,2,3…。現要求將塔座A上的n個圓盤移到塔座C上並仍按同樣的順序疊排,圓盤移動時必須遵守以下規則: (1)每次只能移動一
4.漢諾塔(變)
Description 漢諾塔問題中限制不能將一層塔直接從最左側移動到最右側,也不能直接從最右側移動到最左側,而是必須經過中間。求當有N層塔的時候移動步數。 Input 輸入的第一行為N。 Output 移動步數。 Sample Input 1 2 S
漢諾塔(Hanoi)問題遞迴&非遞迴的C++實現及總結
漢諾塔(Hanoi)問題遞迴&非遞迴的C++實現及總結 由於剛入門不算很久,所以就那漢諾塔這種簡單問題來練下手啦~~ 【漢諾塔問題內容】(雖然路人皆知但還是寫一下好了。。。) 相傳在古印度聖廟中,有一種被稱為漢諾塔(Hanoi)的遊戲。
漢諾塔(C的經典遞迴習題)
漢諾塔問題:設有三個塔座,依次命名為 x,y,z 。有 z 個直徑不同的圓盤,由小到大依次 編號為 1 、 2 、 …… , n 。開始時,它們全部按遞減的次序插在塔座上。現
c語言實現漢諾塔(程式執行步驟詳解)
很久沒去接觸c語言了,今天翻了翻c語言的書,偶然間看到了大一時讓我鬱悶了很久的漢諾塔問題,又重新推理了一遍,漢諾塔的實現採用遞迴演算法,涉及到資料結構中的棧的知識。下面是c實現漢諾塔的原始碼。程式只是實現了文字資訊,即用文字描述了圓盤的移動過程,並未真正實現圓盤的移動,該程式