0.題目描述

羅馬數字包含以下七種字元: I， V， X， L，C，D 和 M。

例如， 羅馬數字 2 寫做 II ，即為兩個並列的 1。12 寫做 XII ，即為 X + II 。 27 寫做  XXVII, 即為 XX + V + II 。

通常情況下，羅馬數字中小的數字在大的數字的右邊。但也存在特例，例如 4 不寫做 IIII，而是 IV

• I 可以放在 V (5) 和 X (10) 的左邊，來表示 4 和 9。
• X 可以放在 L (50) 和 C (100) 的左邊，來表示 40 和 90。 
• C 可以放在 D (500) 和 M (1000) 的左邊，來表示 400 和 900。

給定一個羅馬數字，將其轉換成整數。輸入確保在 1 到 3999 的範圍內。

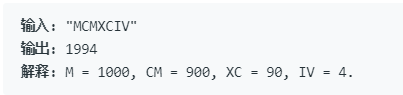
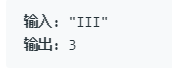
分析：首先字串逐個讀取方式：比如S="IIV",那麼S[0]="I",S[1]="I",S[2]="V"。

             字串長度：S.length()。

1.解析

這道題情況較少，題目比較簡單，思路是首先建立各個字母與數字的雜湊表對映。然後迴圈，

當i=0的時候，第一次迴圈，這時候不可能出其他意外情況，所以單獨拿出來。

當i大於等於1的時候，這時候就需要判斷是否是六種情況以內的情況。我們分析六種情況可得，其實這六種情況都可以用1種表示式表示：IV=I+V-2I ; LX=L+X-2L ;CM=C+M-2C.........

所以我們建立hash對映有這種好處，當判斷出這六種情況時，都適用於這一個公式：

a += hash[s[i]] - hash[s[i - 1]] * 2;

所以程式碼如下：

class Solution {
public:
    int romanToInt(string s) {
        
    map<char, int> hash;
    hash['I'] = 1;
	hash['V'] = 5;
	hash['X'] = 10;
	hash['L'] = 50;
	hash['C'] = 100;
	hash['D'] = 500;
	hash['M'] = 1000;
    int a = 0;
	for (int i=0; i < s.length(); i++)
	{
		if (i>0)
		{
			if ((s[i] == 'V'&&s[i - 1] == 'I') || (s[i] == 'X'&&s[i - 1] == 'I') || (s[i] == 'L'&&s[i - 1] == 'X') || (s[i] == 'C'&&s[i - 1] == 'X') || (s[i] == 'D'&&s[i - 1] == 'C') || (s[i] == 'M'&&s[i - 1] == 'C'))
				a += hash[s[i]] - hash[s[i - 1]] * 2;
			else
				a += hash[s[i]];

		}
		else
			a += hash[s[i]];
	}
        
        return a;                      
    }
};

這道題迴圈次數為n，迴圈裡面每一步常數時間複雜度，所以整體時間複雜度為O[n]。

時間如下：