NLP --- 隱馬爾可夫HMM(概念詳解)
本節將進入隱馬爾可夫環節,再次提醒不懂馬爾科夫過程的同學建議先搞懂什麼是馬爾科夫過程,什麼是馬爾科夫鏈,同時需要懂一點語言模型的知識,下面會用到一點點,本人打算詳細總結隱馬爾可夫演算法思想,因此講解的會很詳細,就意味著我會分幾部分來講,大概思路是先通過淺顯易懂的示例引入隱馬爾可夫概念,然後給出語音識別的例子引出隱馬爾可夫的相關概念和性質,在此基礎上深入挖掘HMMs的演算法原理和使用過程,以及學習演算法思想等等,好,下面正式開始今天的內容。
HMM概念(Hidden markov model)
宗成慶的書裡介紹了,利用語言模型進行語音識別的例子,這裡我們來簡單的看一下這個簡單的語音識別是如何使用語言模型進行判別的,他有哪些缺點?這裡我們輸入是一句話的拼音,要求輸出對應的漢子,這就是最簡單的語音識別了:
輸入: ta shi yan jiu wu li de
輸出:塔 是 研究物理的
他式菸酒屋裡的
利用語言模型怎麼求呢?其實很簡單,就是遍歷每個發音多對應的字,然後求出一句話的概率,這樣就會求出很多概率的集合,那麼我們從中選擇概率最大的句子作為輸出,這裡的難點在哪裡呢?難點在計算量上,即每個發音都有很多候選項,例如ta的候選項就有他、它、塔、她、踏、塌、、、等等很多,整個句子的拼音每一個都對應很多的候選項,一旦組合就會出現很多種可能的情況,計算量可想而知,這還是簡單的一個句子,如果是很多很長的句子,計算量會呈現指數級增長的,因此語言模型無法解決語音識別的問題,我們就需要研究出更適合語音識別的複雜模型,這時隱馬爾可夫就順勢而生了,我們看看隱馬爾可夫是如何解決語音識別的問題的。其實很簡單,語言模型在計算概率時每個拼音對應的字是獨立的即前後沒什麼關聯性,我們知道,我們說的話都和上下文有關的,在常用5000漢子集了,這些漢字的組合大部分都是稀疏的即不能組合的,例如“我們”配對的概率很大,但是“我門”配對的概率很小,基於此HMM模型就根據前面一個或多個字進行對本時刻的發音進行識別,因此可用性很好,從常識中我們也可以很輕鬆的感受到HMM要比語言模型好很多。到這裡我們知道了隱馬爾可夫在語音識別的思想了,但是具體他是怎麼工作的呢?我們下面就開始來看看。
這裡先把隱馬爾可夫的定義給出,然後在通過舉例進行詳細講解:
一般的,一個HMM記為一個五元組,其中,S為狀態的集合,K為輸出符號的集合,
分別是初始狀態的概率分佈、狀態轉移概率和符號發射概率,為了簡單,有時也將其記為三元組
。下面給大家解釋定義都代表什麼意思:
首先你應該知道什麼是馬爾科夫鏈,知道什麼是轉移概率,什麼狀態,這是你理解下面內容的前提:

在馬爾科夫鏈中,我們有狀態轉移過程,此過程是可見的即我們可以觀察到,如上圖的狀態轉移圖,而在隱馬爾科夫中的狀態轉移過程是不可見的如上圖的隱藏序列,這裡的狀態轉移概率使用矩陣表示(和馬爾科夫鏈一樣的) ,
是初始的狀態概率分佈。但是我們在狀態轉移過程中每個狀態會發射一個符合集合中的一個符號,這裡我們把符合集合稱為K,其中
,把狀態集合稱為S,其中
,這裡還需要強調的是在狀態轉移的過程中,每到達一個狀態就會發射一個符號,這個符號來自符號集合K的任意一個可能情況,因此這裡把狀態發射的符號的概率集合稱為發射概率矩陣
,這個矩陣
是什麼樣呢?如下:

即每個狀態都會發射符號集合K中的一個符號,這個符號和發射的概率有關,如在s1狀態可能發射的概率為0.01,可能發射
的概率為0.08,,,,但是總的概率是1,如上圖所示 。
這裡需要強調的是在在隱藏序列裡的狀態可以發射符號,例如隱藏序列的s1狀態發射的符號是,我們可以觀察到的是
,但是我們不知道這是哪個狀態發射的,這裡有點繞,就我們從可觀察的序列中的一個符號無法直接得到是哪個狀態發射的,這裡大家需要理解好。
這裡大家可能還會暈暈的,下面我們開始舉例子,第一個例子是擲骰子,第二個例子就是我們剛開始簡單的語音識別的例子。
擲骰子:
假設我手裡有三個不同的骰子。第一個骰子是我們平常見的骰子(稱這個骰子為D6),6個面,每個面(1,2,3,4,5,6)出現的概率是1/6。第二個骰子是個四面體(稱這個骰子為D4),每個面(1,2,3,4)出現的概率是1/4。第三個骰子有八個面(稱這個骰子為D8),每個面(1,2,3,4,5,6,7,8)出現的概率是1/8。

假設我們開始擲骰子,我們先從三個骰子裡挑一個,挑到每一個骰子的概率都是1/3。然後我們擲骰子,得到一個數字,1,2,3,4,5,6,7,8中的一個。不停的重複上述過程,我們會得到一串數字,每個數字都是1,2,3,4,5,6,7,8中的一個。例如我們可能得到這麼一串數字(擲骰子10次):1 6 3 5 2 7 3 5 2 4
這串數字叫做可見狀態鏈。但是在隱馬爾可夫模型中,我們不僅僅有這麼一串可見狀態鏈,還有一串隱含狀態鏈。在這個例子裡,這串隱含狀態鏈就是你用的骰子的序列。比如,隱含狀態鏈有可能是:D6 D8 D8 D6 D4 D8 D6 D6 D4 D8
一般來說,HMM中說到的馬爾可夫鏈其實是指隱含狀態鏈,因為隱含狀態(骰子)之間存在轉換概率(transitionprobability)。在我們這個例子裡,D6的下一個狀態是D4,D6,D8的概率都是1/3。D4,D8的下一個狀態是D4,D6,D8的轉換概率也都一樣是1/3。這樣設定是為了最開始容易說清楚,但是我們其實是可以隨意設定轉換概率的。比如,我們可以這樣定義,D6後面不能接D4,D6後面是D6的概率是0.9,是D8的概率是0.1。這樣就是一個新的HMM。
同樣的,儘管可見狀態之間沒有轉換概率,但是隱含狀態和可見狀態之間有一個概率叫做輸出概率(emission probability)。就我們的例子來說,六面骰(D6)產生1的輸出概率是1/6。產生2,3,4,5,6的概率也都是1/6。我們同樣可以對輸出概率進行其他定義。比如,我有一個被賭場動過手腳的六面骰子,擲出來是1的概率更大,是1/2,擲出來是2,3,4,5,6的概率是1/10。


上面就是簡單的擲骰子的例子,這個例子在後續的講解中還需用到,大家需要好好理解,下面在舉一個例子是關於語音識別的,當然了下面的例子在後面也是會用到的,所以大家需要留意呀。
語音識別:
上面的例子沒有實際意義,所以理解起來可能還是有點困難,這裡使用語音識別的例子可能會更好的闡釋隱馬爾可夫的定義:
我們知道,所謂語意識別其實就是根據拼音推算出漢子,而常用的漢子有5000多個,這些漢字裡的組合很多都是稀疏的,所謂稀疏就是不能組合的例如“天屎”、“黴麗”等,如下圖,在常用的組合中我們通過語料庫進行計算他們之間的概率,如下是比如漢字間的轉移狀態,這個狀態大概有5000左右,他們之間有轉移概率,這個概率是通過語料庫計算得到的,例如“我們”,我和們的轉移概率達到0.5,因此這些狀態構成的轉移矩陣將達到5000x5000的規模,其實下圖就是我們之前說的概率圖模型了又叫狀態轉移圖。
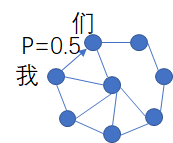
好,上面我們就介紹完了語料庫的問題,也就是說狀態轉移矩陣已經知道了,下面我們詳細看看隱馬爾可夫的是如何工作的:

上面的拼音是可觀察的發射符號,隱藏的是我們未知的序列,現在我們需要通過可觀察的符號序列去計算隱藏的序列,也就是去計算狀態的轉移過程,這就是其中一個隱馬爾可夫需要解決的問題,這裡大家通過這幾個例子應該可以清晰的理解隱馬爾可夫的工作過程了吧,這裡為了方便,我把上面的定義在拿下來大家再看看:
一般的,一個HMM記為一個五元組,其中,S為狀態的集合,K為輸出符號的集合,
分別是初始狀態的概率分佈、狀態轉移概率和符號發射概率,為了簡單,有時也將其記為三元組
。
當考慮潛在事件隨機的生成表面事件時,HMM是非常有用的,假設給定模型,那麼觀察序列
可以由下面的步驟直接產生:
(1)根據初始狀態的概率分佈選擇一個初始狀態
;
(2)設t=1;
(3)根據狀態的輸出概率分佈
輸出
;
(4)根據狀態轉移概率分佈,當前時刻t的狀態轉移到新的狀態
;
(5)t = t+1,如果t<T,重複執行步驟(3)和(4),否則解釋演算法。
好,上面就是對隱馬爾可夫的概念性的介紹了,希望大家能深入理解隱馬爾可夫的工作原理,他和馬爾科夫有什麼聯絡和區別,大家心裡應該有數,另外就是多思考,多總結,本節就到這裡,下一節將主要講解隱馬爾可夫的三個基本問題,然後圍繞這上基本問題進行展開講解。
參考書籍:宗成慶的《統計自然語言處理》
