【數學】【其他】數學中常用符號
寫在前面
對於數學中的一些符號的解釋
整理自網路
持續更新
來源標註為主要來源,個人整理的部分很多
目錄 |
/'deltə/
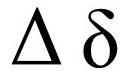
Alt+小鍵盤42660
Alt+小鍵盤42692
Δ在數學中,在一元二次方程ax2+bx+c == 0(a≠0)或二次函式y == ax2+bx+c(a≠0)中代表b2-4ac
Δ在物理學中,表示物理量的變化
δ在數學和科學,表示變數的變化
δ也表示數學中兩個函式
克羅內克δ函式
狄拉克δ函式
——bia度知道
/'zi:tə/

Alt+小鍵盤42694
數學上,有多個名為ζ函式的函式,最著名的是黎曼ζ函式
——bia度百科
/'i:tə/
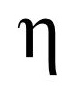
Alt+小鍵盤42695
在物理上, η用作光學上,介質的折射率,用在力學上,表示機械效率,又表示熱機效率
在統計學上, η用作偏回歸係數
——bia度百科
/'θi:tə/
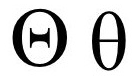
Alt+小鍵盤42664
Alt+小鍵盤42696
Θ可以表示內維爾Θ函式
大Θ符號也是大O符號和大Ω符號的結合
設函式f(n)代表某一演算法在輸入大小為n的情況下的工作量(效率),則在n趨向很大的時候,我們將f(n)與另一行為已知的函式g(n)進行比較:
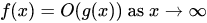
若lim f(n)/g(n) == 0 則稱f(n)在數量級上嚴格小於g(n),記為f(n)=O(g(n))
若lim f(n)/g(n) == ∞ 則稱f(n)在數量級上嚴格大於g(n),記為f(n)=Ω(g(n))
若lim f(n)/g(n) == c (c為非零常數) 則稱f (n)在數量級上等於g(n),即f (n)和g(n)是同一個數量級的函式,記為f(n)=Θ(g(n))
θ在數學上常代表平面的角
——演算法之道(第2版)
——wikipedia
/'læmdə/

Alt+小鍵盤42699
Half-Life
線性代數中的特徵值
Lambda表示式
——bia度百科
/mju:/

Alt+小鍵盤42700
μ,即微(micro-) ,是國際單位制詞頭,指10−6,一百萬分之一
在數學中用於表示莫比烏斯函式
莫比烏斯函式規定:
μ(1) == 1
μ(d) == (-1)k (d為k個不相同素數的積)
μ(n) == 0 (n為除了以上兩種情況外的所有整數)
——https://blog.csdn.net/zhouyuheng2003/article/details/78086543
/əumaik'rɒn/

Alt+小鍵盤42671
大O符號,數學上用於描述函式漸進行為的符號
它是用另一個(通常更簡單的)函式來描述一個函式數量級的漸近上界
常用於大O表示法,見上Θ和θ
——bia度百科
/pai/
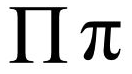
Alt+小鍵盤41415
Alt+小鍵盤42704
π表示圓周率,即圓的周長與直徑的比
Π是π的大寫,是求積符號,累項相乘,使用格式和∑完全相同
在數學中,π(n)表示不大於n的素數個數
——bia度知道
/'sigmə/
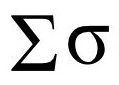
Alt+小鍵盤41414
Alt+小鍵盤42706
∑符號表示求和,讀音為sigma

其中i表示下界,n表示上界, k從i開始取數,一直取到n,全部加起來
這樣表達也可以( ∑ i ),表示對i求和,i是變數
不帶上下標的∑常用於表示迴圈和,∑f(a,b,c) == f(a,b,c) + f(b,c,a) + f(c,a,b)
∑cyc是輪換對稱求和
如:∑(cyc)x²y=x²y+y²z+z²x
(有多項式f(x1,x2,……,xn),滿足f(x1,x2,……,xn) == f(x2,x3,……,x1) == …… == f(xn,x1,……,xn-1),即稱為輪換多項式)
∑sym是對稱求和
如:∑(sym)x²y=x²y+x²z+y²x+y²z+z²x+z²y
(有多項式f(x1,x2,……,xn),設x1',x2',……,xn'是x1,x2,……,xn的任意一個排列,都有f(x1',x2',……,xn') == f(x1,x2,……,xn),則稱它為對稱多項式)
σ可代表標準偏差
σ(n)表示整數n的所有正因數的和
——bia度百科
/fai/
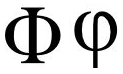
Alt+小鍵盤42677
Alt+小鍵盤42709
Φ與φ這兩個符號有好多意思:
①黃金分割的符號
②複數的軛數
③立體座標中,一直線與 z-軸之間的夾角
④尤拉函式φ(n)
⑤三角函式如y=Asin(ωx+φ)中表示初相(向左向右平移)
不清楚在數學上這兩個符號的區別額
——bia度百科
/psai/

Alt+小鍵盤42711
斐波納契常數的倒數和
代表程式的返回值
——bia度百科
/'oumigə/
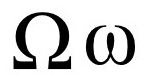
Alt+小鍵盤42680
Alt+小鍵盤42712
Omega (TeX)
Ω可表示首個不可數的序數
朗伯W函式的別稱Ω函式
Ω常數
蔡廷常數
三角函式如y=Asin(ωx+φ)中表示函式在y軸方向的壓縮程度
——bia度百科

MOD,同餘符號
在數學上,兩個整數除以同一個整數,若得相同餘數,則二整數同餘
兩個整數a,b,若它們除以整數m所得的餘數相等,則稱a,b對於模m同餘
記作 a ≡ b (MOD m) 讀作a同餘於b模m,或讀作a與b關於模m同餘
與MOD函式(%)區別開
MOD(同餘符號)的結果必定為正
MOD(函式)的結果可以為負
MOD函式:
①能整除時,其值為0
②不能整除時,其值=除數×(整商+1)-被除數
MOD(負,正) == 正
MOD(正,負) == 負
——bia度百科
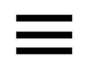
Alt+小鍵盤41428
這個符號有好多意思:
①全等於,可寫為≌
②恆等於
③等價於,可寫為
④同餘符號,見MOD
⑤隨機數
——bia度百科
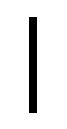
整除符號
若整數b除以非零整數a,商為整數,且餘數為零, 我們就說b能被a整除(或說a能整除b)
b為被除數,a為除數,即a|b,讀作“a整除b”或“b能被a整除”
位運算“位或”
——bia度百科
/sʌm/
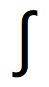
Alt+小鍵盤41426
∫是數學的一個積分
——bia度百科
/fai/

Alt+小鍵盤41427
閉合曲線積分
——bia度百科
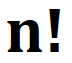
n!表示階乘
正整數n的階乘的計算:
![]()
——bia度百科

!n表示精神錯亂錯排
| In combinatorial mathematics, a derangement is a permutation of the elements of a set, such that no element appears in its original position. In other words, derangement is a permutation that has no fixed points. |
| 譯: 在組合數學中,錯排是集合中元素的排列,使得沒有元素出現在其原始位置 換言之,錯排是沒有不變元素的排列 |
有n個元素的集合的的全排列中,錯排的計算: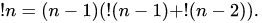
——wikipedia
