Dynamic ：我們認為問題是擁有某種時間或者順序方面的特性。

Programming：這裡我們討論的是數學規劃，就像是線性規劃，或者是二次規劃。

動態規劃能夠幫助我們解決一些複雜的問題，就是將複雜的問題分解成子問題，然後去解決這些子問題，將這些子問題的答案結合起來，最終得到原問題的答案。

使用動態規劃的方法需要滿足兩個特性：

1.最優結構：最優化原理，說的是我們可以將某些整體性問題，分解成兩個或者多個的子問題，子問題的最優解也就是整體的最優解。簡要來說就是整個優化問題可以分解為多個子優化問題。

2.重複的問題：子問題是重複的，這樣我們就可以不斷重複獲得子優化問題的解，使得我們可以將子優化問題的解重複利用。

馬爾可夫決策過程是滿足動態規劃的兩個條件的，除此之外，馬爾可夫決策過程也滿足貝爾曼方程。貝爾曼方程就是遞迴組合，其中我們將最優值函式拆分兩部分，第一步是最優行為，以及在此之後的最優行為。你可以理解為目前的一步行動是最好的，餘下的其它步驟也將採取最優的行動，這些就組成了整體的最優值。

我們可以認為Value function就是快取目前我們所找到MDP的最優值資訊。通過value function 我們可以找到從任一狀態出發的解決方案。通過value function函式，我們可以找到最優的行動方式。並以那個狀態為起點，得到最大獎勵。一旦你得到了最優獎勵，就可以進行回溯。

這裡我們說兩個特殊案例的解決方案：

預測問題：

這個問題就是我們知道了一個標準的MDP，我們同時也知道了Policy。我想知道我將會得到多少獎勵？針對這個問題，我們需要求解的就是value function，通過value function，我們就可以得到我們能獲得的最大獎勵是多少。實際上這也是policy評估，通過他我們能知道policy的效果如何。

控制問題：

在這個問題中我們也是知道了MDP的所有資訊，像Atari遊戲，我們需要知道遊戲內部所有的資料，每一步將要產生的資料我們都知道，我們現在想做的就是控制這個遊戲，但是我們並不知道policy。我們想知道的是最好的策略是什麼？我們想要知道在所有的策略中我們選擇哪一個才能得到最多的獎勵。也就是找一個最好的狀態到動作的對映。

Policy Evaluation

上節課我們是得到了狀態值函的計算公式，狀態s處的值函是是可以利用後繼的值函式V（s'）來表示的。通過高斯-賽德爾迭代演算法，我們就可以對其進行求解，結果如上圖中的公式所示。上面這個方程代表的是值函式的期望形式。

向前看一步，我們向前看的是下一個狀態的值。採用貝爾曼方程，每當我們向前看一步，那麼我們就得到了下個狀態的值，我們所有可能採取的動作都考慮進去，得到接下來的狀態，我們考慮這些連續狀態的value，在得到下個時刻每一個狀態的概率之後，我們將其備份，這樣我們就知道了路徑上的value值和其對應概率了。

之後的話我們就可以對其進行計算代。我們在葉節點儲存我們先前的迭代value。以便我們求得下一次迭代的value，也就是我們想要得到value函式。我們需要最近一次迭代k，將k迭代產生的值帶入方程中，得到葉節點的值。通過這些值，我們就能計算出下一次迭代所產生的一個新的value。我們對每個狀態都做上述操作，我們就可以將所有狀態進行更新求解。

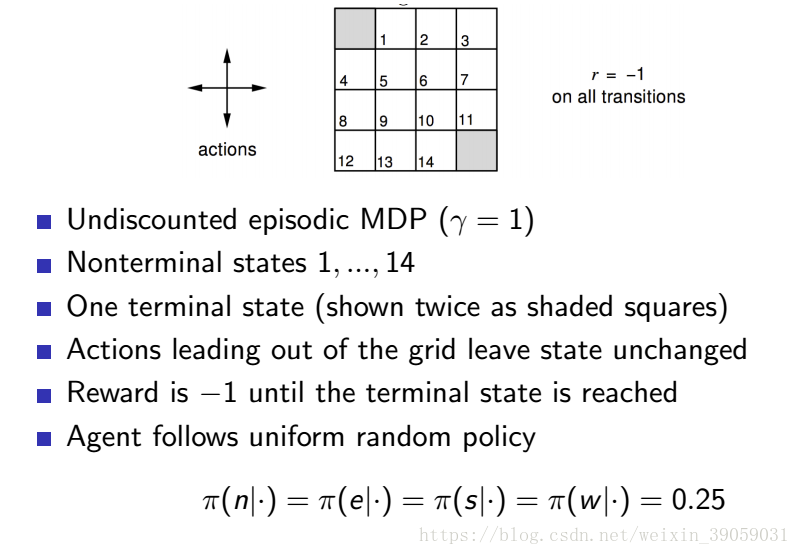
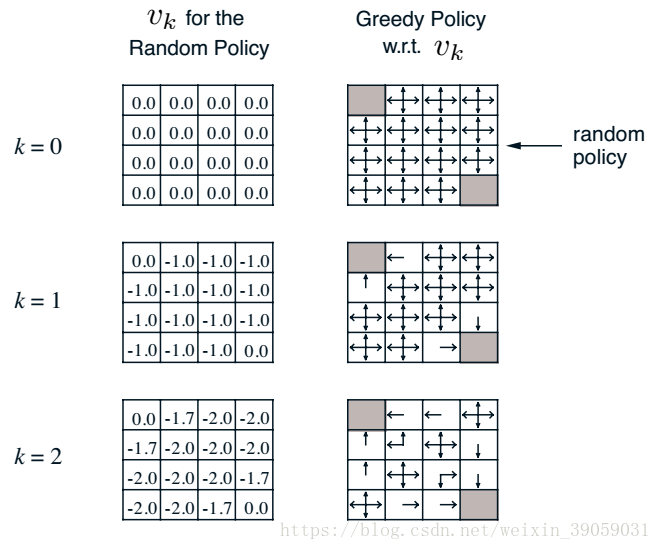
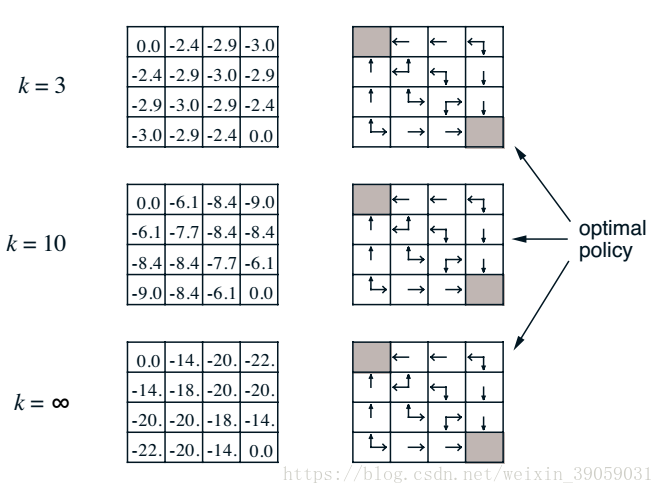
下面舉個例子說明一下：

上圖是遊戲的機制：我們對其迭代求解有：

漸漸地，我們發現值函式最終會收斂，也就是當我們策略隨機的時候，我們最終到達終點的步長將會是20左右。右側的表格就是我們在知道value 函式之後構建的新的policy。如果我們忽略右側的表格，我們可以通過這種策略迭代的方法知道目前我所使用的policy的value。這種方法實際上就是在迭代貝爾曼方程。

Policy Iteration

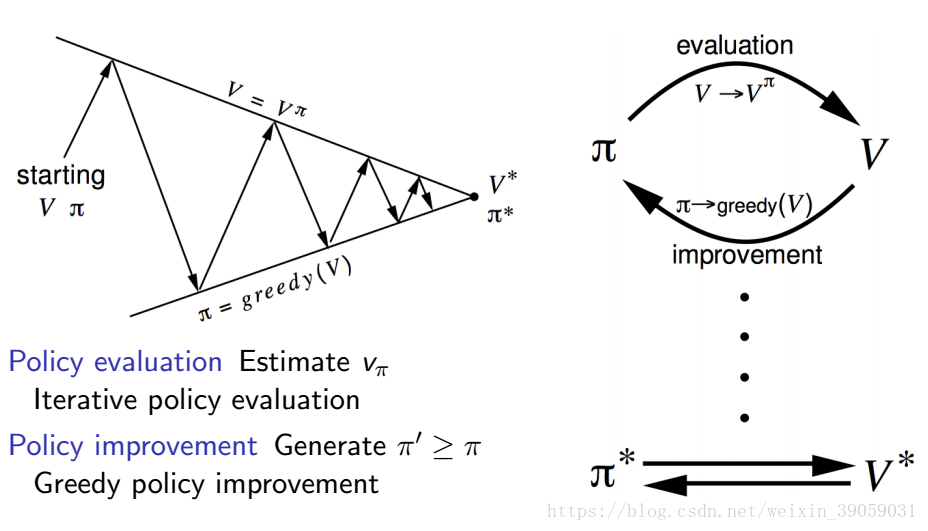
之前我們採取Policy Evaluation的方法能夠去評估一個policy。現在我們想要在MDP過程中，尋找一個儘可能好的policy。我們想通過反饋的方式來將其實現。假設某人已近給了你一個policy，你怎麼樣才能返回一個policy，確保這個policy比原來那個要好。

我們將這個過程分成兩部分，第一部分我們將評估這個給定policy的value函式，就像我們在上面policy evaluatioin說的那樣，給定一個隨機策略，然後更新我們的value函式。第二部分我們依據value函式來改進我們的策略，這裡大多數是採用貪心演算法（大部分動作的選擇採取值函式最大的那一個，小部分採取隨機選擇）。我們通過第一部分->第二部分->第一部分····這樣迭代之後，我們就將會尋找到一個最優的策略。

上面的問題概括起來的話就是下面這張圖片：

那麼我們現在就推到一下整個策略迭代將會收斂，如下圖所示：

我們採用貪婪策略，每次都選取能獲得最大價值的那個動作，那麼我們得到的獎勵至少是和之前的獎勵一樣大的。通過這樣的一次一次迭代之後，我們將會得到一個最優解。

Value Iteration

和策略迭代一樣，值函是迭代也是通過回溯的方式來更新整個值函式的。和policy iteration不同的是，我們每一步並不會使用一個已近確定下來的policy，我們只會直接作用於value空間。只有value函式的迭代。

演算法的更新過程如下圖所示：

其實跟策略迭代沒啥多大區別，一個是把動作加進去取max，一個是還沒有加動作取max。