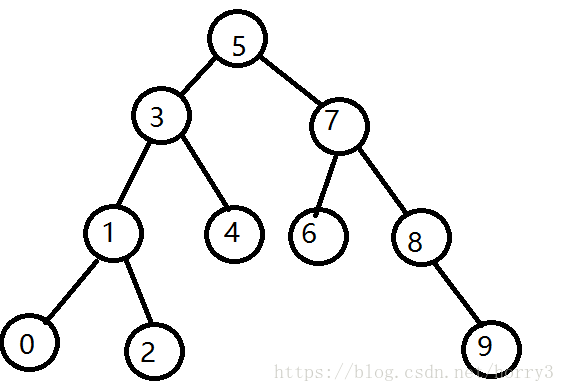
二叉搜尋樹又稱二叉排序樹，他或者是一顆空樹，或者是具有以下性質的二叉樹

1、若它的左子樹不為空，左子樹上所有節點的值都小於根節點上的值

2、若它的右子樹不為空，右子樹上所有節點的值都大於根節點上的值

它的左右子樹分別為二叉搜尋樹

用搜索關鍵字的方法先定義

typedef int Key;

在定義結構體：

typedef struct BSTreeNode{
	Key		key;
	struct BSTreeNode *left;
	struct BSTreeNode *right;
}	BSTreeNode;

先查詢是否由此關鍵詞 如果找到了，返回 0 表示成功 如果沒找到，返回 -1 表示失敗

用遞迴的方法來寫就是

int BSTreeSearch(BSTreeNode *root, Key key)
{
	if (root == NULL) {
		return -1;
	}

	if (key == root->key) {
		return 0;
	}
	else if (key < root->key) {
		return BSTreeSearch(root->left, key);
	}
	else {
		return BSTreeSearch(root->right, key);
	}
}

非遞迴的是：

int BSTreeSearchLoop(BSTreeNode *root, Key key)
{
	BSTreeNode *cur = root;
	while (cur != NULL) {
		if (key == cur->key) {
			return 0;
		}
		else if (key < cur->key) {
			cur = cur->left;
		}
		else {
			cur = cur->right;
		}
	}

	return -1;
}

 

在二叉樹中插入一個關鍵字，要改變引數，所以要傳地址用　 ＊＊ 如果重複，插入失敗， 返回 -1 如果不重複，插入成功， 返回 0

非遞迴方法

int BSTreeInsertLoop(BSTreeNode **pproot, Key key)
{
	assert(pproot != NULL);
	BSTreeNode *cur = *pproot;
	BSTreeNode *parent = NULL;

	while (cur != NULL) {
		if (key == cur->key) {
			// key 重複 插入失敗。
			return -1;
		}

		parent = cur;
		if (key < cur->key) {
			cur = cur->left;
		}
		else {
			cur = cur->right;
		}
	}

	BSTreeNode *node = (BSTreeNode *)malloc(sizeof(BSTreeNode));
	node->key = key;
	node->left = NULL; node->right = NULL;

	if (parent == NULL) {
		// 對空樹做插入
		*pproot = node;
	}
	else if (key < parent->key) {
		parent->left = node;
	}
	else {
		parent->right = node;
	}

	return 0;
}

 

遞迴法

int BSTreeInsert(BSTreeNode **pproot, Key key)
{
	if (*pproot == NULL) {
		BSTreeNode *node = (BSTreeNode *)malloc(sizeof(BSTreeNode));
		node->key = key;
		node->left = NULL; node->right = NULL;
		*pproot = node;
		return 0;
	}

	if (key == (*pproot)->key) {
		return -1;
	}

	if (key < (*pproot)->key) {
		return BSTreeInsert(&(*pproot)->left, key);
	}
	else {
		return BSTreeInsert(&(*pproot)->right, key);
	}
}

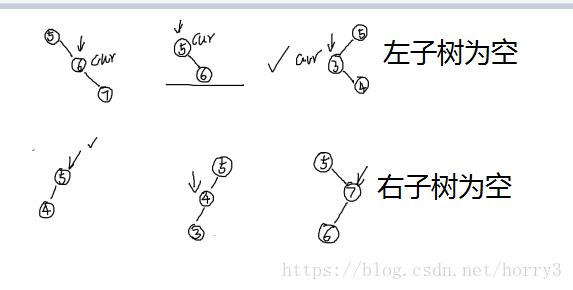
刪除關鍵字： 如果找到了，就成功刪除，返回０ 如果沒有找到，就返回－１ 刪除的時候分為三種情況

int BSTreeRemoveLoop(BSTreeNode **pproot, Key key)
{
	BSTreeNode *cur = *pproot;
	BSTreeNode *parent = NULL;
	while (cur != NULL) {
		if (key == cur->key) {
			// 真正刪除
			if (cur->left == NULL) {
				if (parent == NULL) {
					// 要刪除的是根結點
					*pproot = cur->right;
				}
				else if (key < parent->key) {
					parent->left = cur->right;
				}
				else {
					parent->right = cur->right;
				}
				free(cur);
				return 0;
			}
			else if (cur->right == NULL) {
				if (parent == NULL) {
					// 要刪除的是根結點
					*pproot = cur->left;
				}
				else if (key < parent->key) {
					parent->left = cur->left;
				}
				else {
					parent->right = cur->left;
				}
				free(cur);
				return 0;
			}
			else {
				// 替換法刪除
				// 左右孩子都不為空

				// 找右子樹中最小的一個
				BSTreeNode *del = cur->right;
				BSTreeNode *delParent = cur;
				while (del->left != NULL) {
					delParent = del;
					del = del->left;
				}

				cur->key = del->key;

				if (delParent == cur) {
					delParent->right = del->right;
				}
				else {
					delParent->left = del->right;
				}
				free(del);
				return 0;
			}
		}

		parent = cur;
		if (key < cur->key) {
			cur = cur->left;
		}
		else {
			cur = cur->right;
		}
	}

	return -1;
}