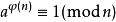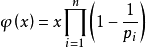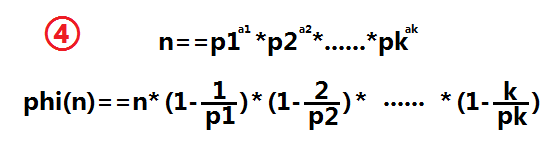【數學】【數論】初探尤拉定理
阿新 • • 發佈:2018-12-16
寫在前面:
記錄了個人的學習過程,同時方便複習
整理自網路
非原創部分會標明出處
目錄
|
| 在數論中,尤拉定理(也稱費馬-尤拉定理或尤拉函式定理)是一個關於同餘的性質 尤拉定理表明,若n,a為正整數,且n,a互質,則:
——bia度百科 |
(某一種證法)
將1~n中與n互質的數按順序排布:x1,x2……xφ(n) (顯然,共有φ(n)個數)
| 尤拉函式 在數論,對正整數n>1,尤拉函式是小於n的正整數中與n互質的數的數目(φ(1)=1)
(其中p1, p2……pn為x的所有質因數,x是不為0的整數) ——bia度百科
|
我們考慮這麼一些數:
m1 == a*x1 m2 == a*x2 m3 == a*x3 …… mφ(n) == a*xφ(n)
1)這些數中的任意兩個都不模n同餘,因為如果有mS ≡ mR (MOD n) (這裡假定mS 更大一些),就有:
mS - mR == a(xS - xR) == qn,即n能整除a(xS - xR)
但是a與n互質,而xS - xR<n,因而左式不可能被n整除
也就是說這些數中的任意兩個都不模n同餘,φ(n)個數有φ(n)種餘數
——bia度百科
- 簡化冪的模運算
如計算7222的個位數,實際是求7222被10除的餘數
7和10互素,且φ(10)=4
由尤拉定理知74 Ξ 1 (MOD 10)
所以7222 == (74)55 * (72) Ξ 155 * 72 Ξ 49 Ξ 9 (mod 10)
——bia度百科