彩色影象處理有兩個主要鄰域：一個是全綵色處理，通常要求影象用全綵色感測器獲取；另一個是偽彩色處理，它是對一種灰度會灰度範圍賦予一種顏色。

數字影象處理中，常用發模型是RGB(紅、綠、藍)模型和HSI(色調、飽和度、亮度)模型，其中HSI模型可以解除影象中顏色和灰度資訊的聯絡，使其更適合許多灰度處理技術。

RGB彩色模型(紅、綠、藍)

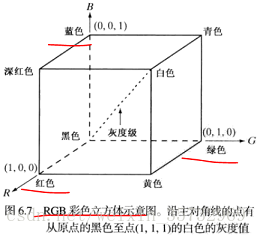
RGB彩色模型基於笛卡爾座標系，並假設所有顏色值都歸一化了，即R、G、B的所有值都假定在範圍[0,1]內。彩色子空間是如下圖的立方體：

在RGB彩色模型中，用於表示每個畫素的位元數稱為畫素深度。如果一幅RGB影象，其中每一幅紅、綠、藍影象都是一幅8位元影象，則每個畫素有24位元的深度。全綵色影象通常用來表示一幅24位元的GRB彩色影象。

HSI彩色模型(色調、飽和度、亮度)

色調是描述一種純色（純黃色，純橙色，純紅色）的顏色屬性；飽和度是一種純色被白光稀釋的程度的度量；亮度是主觀的描述子，實際上是不可度量的，體現了無色強度概念。而強度（灰度級）是單色影象最有用的描述子，是可以度量的。HSI彩色模型可以從彩色資訊中消去強度分量的影響。

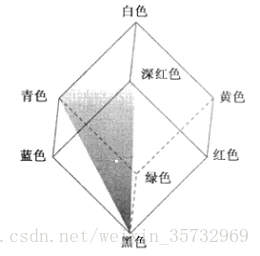
考慮前面提到的彩色立方圖，強度（灰度級）是沿連線白色定點(1,1,1)和黑色頂點(0,0,0)的直線分佈的，要確定任何彩色點的強度分量，可以通過一個垂直於強度軸幷包含該彩色點的平面，該平面與強度軸的交點就給出了[0,1]內的強度值。並且，一種顏色的飽和度（純度）以強度軸的距離為函式兒增大。強度軸的上的點的飽和度為0，沿著強度軸的所有點都是灰度。

上圖中，顯示了由3個點（黑、白和青）定義的一個平面，可以知道包含在由強度軸和立方體邊界定義的平面段內的所有點都有相同的色調（在這種情況下是青色），因為有如下結論：所有顏色都是由位於這些顏色定義的三角形中的3種顏色產生的。如果這些點中的兩點是黑點和白點，第三點是彩色點，那麼三角形上的所有點都有相同的色調，因為黑白分量不能改色調。我們可以得出這樣的結論：形成SHI空間所要求的色調、飽和度和強度值可由RGB彩色立方體得到。

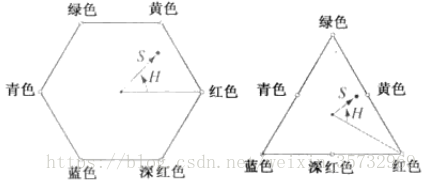
HSI空間由一個強度軸和位於與該強度軸垂直的平面內的彩色點的軌跡表示。當平面沿強度軸上下移動時，由每個平面與立方體表面構成的橫截面定義的邊界不是三角形就是六邊形，如下圖：

通常，與紅軸的0°角指定為0色調，從這開始色調逆時針增長；飽和度（距垂直軸的距離）是從原點到該點的向量長度。HSI彩色模型的重要分量是垂直強度軸、到一個彩色點的向量長度和該向量與紅軸的夾角。

HSI和RGB之間的轉換

從RGB到HSI的彩色轉換：

每個RGB畫素的色調分量H為：

其中，

飽和度分量S為：

強度分量I為：

假定RGB值已歸一化到區間[0,1]內，且角度根據HSI空間的紅軸來度量，則可以把求到的色調H除以360°歸一化到[0,1]內，而其他兩個值已經在[0,1]內。

從HSI到RGB的彩色轉換：

假定HSI值在[0,1]內，把H乘以360°，使色調回到原來的[0°，360°]內。

當H的值在RG扇區，RGB分量為：

當H在GB扇區，首先從H中減去120°，即：

RGB分量為：

當H在BR扇區，首先從H中減去240°，即：

RGB分量為：

偽彩色影象處理

偽彩色影象處理是指基於一種指定的規則對灰度值賦以顏色的處理。

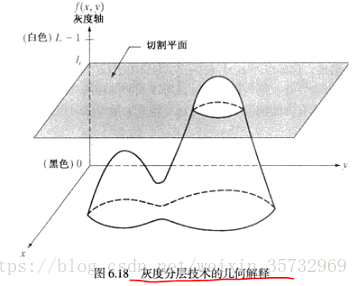
灰度分層：

對上圖中平面的每一側賦以不同的顏色，平面上面的灰度級的畫素將編碼成一種彩色，平面下面的畫素編碼成另一種顏色，平面上的畫素賦以兩種色彩之一。

確切說來，令[0,L-1]表示灰度級，令代表黑色[f(x,y) = 0]，並令代表白色[f(x,y) = L-1]。假定垂直於灰度軸的P個平面定義為灰度級，，P個平面將灰度級分為P+1個區間。灰度級到彩色賦值按如下進行：

其中，是與第k個灰度區間有關的顏色，由位於l = k-1和l=k處的分割平面定義。

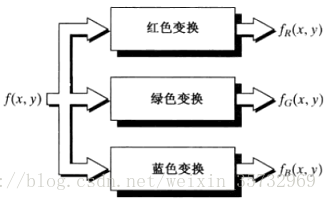
灰度到彩色的變換：對任何輸入畫素的灰度執行3個獨立的變換，然後將3個變換結果分別送入紅綠藍通道，產生一幅合成影象。如下圖：

全綵色影象處理簡介

全綵色影象處理方法分為兩種。一種是分別處理每一幅分量影象，然後把處理結果合成彩色影象；另一種是直接處理彩色影象。RGB彩色空間中的一個任意向量：

彩色分量是座標(x,y)的函式：

對於大小為M*N的影象，有M*N個這樣的向量c(x,y)，其中，x=0,1,2,...,M-1;y=0,1,2,...,N-1。

我們可以用標準的灰度影象處理方法分別處理彩色影象的每一個分量，但這種處理結果並不總等同於彩色空間中的直接處理，這時就要採取新的表達方法。

為了使每種彩色分量處理和基於向量 處理等同，必須滿足兩個條件：1、處理必須對向量和標量都可用；2、對向量每一分量的操作對於其他分量必須是獨立的。如平均操作。